黑龙江省大庆市林甸县2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-09-23 类型:期末考试
一、单选题
-
1. 下列各曲线中,表示y不是x的函数的是( )A、
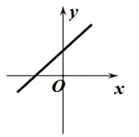 B、
B、 C、
C、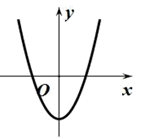 D、
D、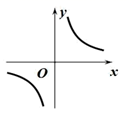 2. 下列数据中不能确定物体位置的是( )A、某市政府位于北京路32号 B、小明住在某小区3号楼7号 C、太阳在我们的正上方 D、东经130°,北纬54°的城市3. 下列各式:① ,② ,③ ,④ 中,最简二次根式有( )A、1个 B、2个 C、3个 D、4个4. 对于一次函数 ,下列结论错误的是( )A、函数的图象与x轴的交点坐标是 B、函数值随自变量的增大而减小 C、函数的图象不经过第三象限 D、函数的图象向下平移4个单位长度得到 的图象5. 下列说法正确的个数有()
2. 下列数据中不能确定物体位置的是( )A、某市政府位于北京路32号 B、小明住在某小区3号楼7号 C、太阳在我们的正上方 D、东经130°,北纬54°的城市3. 下列各式:① ,② ,③ ,④ 中,最简二次根式有( )A、1个 B、2个 C、3个 D、4个4. 对于一次函数 ,下列结论错误的是( )A、函数的图象与x轴的交点坐标是 B、函数值随自变量的增大而减小 C、函数的图象不经过第三象限 D、函数的图象向下平移4个单位长度得到 的图象5. 下列说法正确的个数有()① 的算术平方根是3
②± 是 的平方根
③ =±
④ =0.2
⑤0.1是0.01的一个平方根
A、1个 B、2个 C、3个 D、4个6. 坐标平面上有一点A , 且点A到x轴的距离为3,A点到y轴的距离恰为到x轴距离的3倍.若A点在第二象限,则A点坐标为( )A、 B、 C、 D、7. 如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( ) A、4 B、3 C、2 D、58. 某同学乘游船去观光,已知游船在静水中的速度为15 ,水流速度为5 .游船先从甲地逆水航行到乙地,在乙地停留一段时间后,又从乙地顺水航行返回到甲地,设游船航行的时间为 ,离开甲地的距离为 ,则s与t的函数关系用图象表示大致是( )A、
A、4 B、3 C、2 D、58. 某同学乘游船去观光,已知游船在静水中的速度为15 ,水流速度为5 .游船先从甲地逆水航行到乙地,在乙地停留一段时间后,又从乙地顺水航行返回到甲地,设游船航行的时间为 ,离开甲地的距离为 ,则s与t的函数关系用图象表示大致是( )A、 B、
B、 C、
C、 D、
D、 9. 直线l1:y=kx+b与直线l2:y=bx+k在同一坐标系中的大致位置是( )A、
9. 直线l1:y=kx+b与直线l2:y=bx+k在同一坐标系中的大致位置是( )A、 B、
B、 C、
C、 D、
D、 10. 在直角坐标系中,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有( )A、1个 B、2个 C、3个 D、4个
10. 在直角坐标系中,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有( )A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 函数y= 中自变量x的取值范围是 .12. 已知样本1,3,9,a,b的众数是9,平均数是6,则中位数为.13. 已知点 , , 都在直线 上,则 的值得大小关系是 .14. 已知方程组 和方程组 有相同的解,则m的值是 .15. 平行四边形ABCD中,AE平分∠BAD交BC与点E,且将BC分成4cm和6cm两部分,则平行四边形ABCD的周长为 .16. 如图,在平面直角坐标系中直线y=﹣2x与y=﹣ x+b交于点A,则关于x,y的方程组 的解是 .
 17. 如图是一个三级台阶,它的每一级的长、宽和高分别为20 dm,3 dm,2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是dm.
17. 如图是一个三级台阶,它的每一级的长、宽和高分别为20 dm,3 dm,2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是dm. 18. 如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为
18. 如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为
三、解答题
-
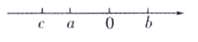
19. 解二元一次方程组:(1)、(2)、20. 若x , y都是实数,且y= + +8,求3x+2y的平方根.21. 已知实数a,b,c在数轴上的位置如图所示,化简: .
 22. 如图,四边形ABCD中,∠B=90°,AB=4,BC=3,CD=13,AD=12,求四边形ABCD的面积.
22. 如图,四边形ABCD中,∠B=90°,AB=4,BC=3,CD=13,AD=12,求四边形ABCD的面积. 23. 一家公司对王强、李莉、张英三名应聘者进行了创新、综合知识和语言三项素质测试,他们的成绩如下表所示:
23. 一家公司对王强、李莉、张英三名应聘者进行了创新、综合知识和语言三项素质测试,他们的成绩如下表所示:测试项目
测试成绩
王强
李莉
张英
专业知识
72
85
67
工作经验
50
74
70
仪表形象
88
45
67
(1)、如果根据三项测试的平均成绩确定录用人选,你选谁?请说明理由;(2)、根据实际需要,广告公司给出了选人标准:将创新、综合知识和语言三项测试得分按6:3:1的比例确定各人的测试成绩.你选谁?请说明理由.24. 3 的小数部分为m,3+ 的小数部分为n,求(m-3)(n+2)的值.25. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)、求每台A型电脑和B型电脑的销售利润;(2)、该商店计划一次购进两种型号的电脑共100台,设购进A型电脑x台,这100台电脑的销售总利润为y元. 求y关于x的函数关系式;26. 甲、乙两名同学在解方程组 时,甲解题时看错了m , 解得 ;乙解题时看错了n , 解得 .请你以上两种结果,求出原方程组的符合题意解.

