吉林省长春市长春汽车经济技术开发区2020-2021学年九年级上学期数学期末试卷
试卷更新日期：2021-09-23 类型：期末考试
一、单选题
-
1. 方程x2-2x=0的根是（ ）A、x1=x2=0 B、x1=x2=2 C、x1=0，x2=2 D、x1=0，x2=-22. 抛物线y＝x2﹣4x+3与y轴交点坐标为（ ）A、(3，0) B、(0，﹣1) C、(2，﹣1) D、(0，3)3. 在一个不透明的布袋中，红色、黑色、白色的玻璃球共有40个，除颜色外其他完全相同，小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率分别稳定在15%和35%，则口袋中白色球的个数可能是（ ）A、6个 B、14个 C、20个 D、40个4. 如图，边长为4的等边△ABC中，DE为中位线，则四边形BCED的面积为（ ）
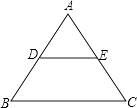A、 B、 C、 D、5. 如图，AB是⊙O的直径，点C、D、E都在⊙O上．若∠1＝55°，则∠2的大小为（ ）
A、55° B、45° C、35° D、25°6. 如图，在平面直角坐标系中，P是第一象限内的点，其坐标是（3，m），且OP与x轴正半轴的夹角α的正切值是 ，则m的值为（ ）
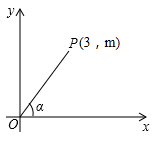A、5 B、4 C、3 D、7. 如图，⊙O与正六边形OABCDE的边OA、OE分别交于点F、G，点M为劣弧FG的中点．若FM＝2 ，则⊙O的半径为（ ）
A、2 B、 C、2 D、8. 如图，在平面直角坐标系中，抛物线 经过坐标原点O，与x轴的另一个交点为A．过抛物线的顶点B分别作BC⊥x轴于点C、BD⊥y轴于点D，则图中阴影部分图形的面积和为（ ）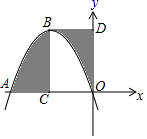
A、18 B、12 C、9 D、6二、填空题
-
9. 计算：tan245°+1＝ ．10. 若关于x的一元二次方程x2+2x+k＝0无实数根，则k的取值范围是 ．11. 如图，在圆内接四边形ABCD中，若∠A＝60°，则∠C的大小为 ．
12. 如图，在 中，点E在边AD上，AE：AD＝2：3，BE与AC交于点F．若AC＝20，则AF的长为 ．
13. 圆心角为90°的扇形如图所示，过 的中点作CD⊥OA、CE⊥OB，垂足分别为点D、E．若半径OA＝2，则图中阴影部分图形的面积和为 ．
14. 在平面直角坐标系中，抛物线y＝x2+bx+5的对称轴为直线x＝1．若关于x的一元二次方程 （t为实数）在﹣1＜x＜4的范围内有实数根，则t的取值范围为 ．三、解答题
-
15. 解方程：x2﹣4x﹣3＝0.16. 有甲、乙两个不透明的口袋，甲袋中有3个球，分别标有数字0，2，3；乙袋中有2个球，分别标有数字1，4，这5个球除所标数字不同外其余均相同．从甲、乙两袋中各随机摸出1个球．用画树状图（或列表）的方法，求摸出的两个球上数字之和是4的概率．17. 图①、图②均是6×6的正方形网格，每个小正方形的顶点称为格点．线段AB的端点均在格点上．只用无刻度的直尺按下列要求在给定的网格中画图，不要求写画法，保留作图痕迹．
(1)、在图①中画出线段AB的中点C；(2)、在图②中画出线段AB上的一点D，使AD：BD＝4：5．18. 如图，航拍无人机从A处测得一幢建筑物顶部B处的仰角为45°、底部C处的俯角为63°，此时航拍无人机A处与该建筑物的水平距离AD为80米．求该建筑物的高度BC（精确到1米）．[参考数据：sin63°＝0.89，cos63°＝0.45，tan63°＝1.96]
19. 在平面直角坐标系中，抛物线y＝ax2＋bx经过点A(2，4)和点B(6，0)．(1)、求这条抛物线所对应的二次函数的解析式；(2)、直接写出它的开口方向、顶点坐标；(3)、点(x1 ， y1)，(x2 ， y2)均在此抛物线上，若x1＞x2＞4，则y1 y2(填“＞”“＝”或“＜”)．20. 如图，在 中，AC＝BC，以BC为直径的⊙O与底边AB交于点D，过点D作DE⊥AC，垂足为点E．
(1)、求证：DE为⊙O的切线；(2)、若BC＝4，∠A＝30°，求 的长．（结果保留π）21. 某山区不仅有美丽风光，也有许多令人喜爱的土特产，为实现脱贫奔小康，该山区组织村民加工包装土特产销售给游客，以增加村民收入．已知某种土特产每袋成本10元，试销阶段每袋的销售价x（元）与该土特产的日销售量y（袋）之间的关系如表：x（元）
15
20
30
……
y（袋）
25
20
10
……
(1)、若日销售量y（袋）是每袋的销售价x（元）的一次函数，求y与x之间的函数关系式；(2)、假设后续销售情况与试销阶段效果相同，设每日销售土特产的利润为w（元）；①求w与x之间的函数关系式；
②要使这种土特产每日销售的利润最大，每袋的销售价应定为多少元？每日销售的最大利润是多少元？
22. 如图，在平面直角坐标系中，抛物线y＝ （x﹣1）2﹣2与x轴交于点A和点B（点A在点B的左侧），第一象限内的点C在该抛物线上．
(1)、直接写出A、B两点的坐标；(2)、若 的面积为12，求点C坐标；(3)、在（2）问的条件下，直线y＝mx+n经过点A、C， （x﹣1）2﹣2＞mx+n时，直接写出x的取值范围．23. 如图，在 中，∠ACB＝90°，AB＝10，AC＝6，点P从点B出发，以每秒5个单位长度的速度沿BC向点C运动，同时点M从点A出发，以每秒6个单位长度的速度沿AB向点B运动，过点P作PQ⊥AB于点Q，以PQ、MQ为邻边作矩形PQMN，当点P到达点C时，整个运动停止．设点P的运动时间为t（t＞0）秒．
(1)、求BC的长；(2)、用含t的代数式表示线段QM的长；(3)、设矩形PQMN与 重叠部分图形的面积为S（S＞0），求S与t之间的函数关系式；(4)、连结QN，当QN与 的一边平行时，直接写出t的值．24. 在平面直角坐标系中，将函数y＝x2﹣2mx+4m（m为常数）的图象记为G，图象G的最低点为P(x0 ， y0)．
(1)、当m＝0时，写出这个函数的表达式，并在所给坐标系中画出对应的图象G．(2)、当y0＝﹣1时，求m的值．(3)、求y0的最大值．(4)、当m＞0，且当图象G与x轴有两个交点时，左边交点的横坐标为x1 ， 直接写出x1的取值范围．