吉林省长春市二道区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是关于 x 的一元二次方程的是（）

A、x+2y＝0 B、x²﹣4y＝0 C、x²+3x＝0 D、x+1＝0

查看试题解析
2. 将 $\sqrt{8}$ 化简后的结果是（）

A、2 B、 $\sqrt{2}$ C、 $2 \sqrt{2}$ D、 $4 \sqrt{2}$

查看试题解析
3. 如图，∠1＝∠2，则下列各式不能说明△ABC∽△ADE的是（）

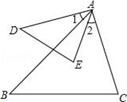A、∠D＝∠B B、∠E＝∠C C、 $\frac{A D}{A B} = \frac{A E}{A C}$ D、 $\frac{A D}{A B} = \frac{D E}{B C}$

查看试题解析
4. “翻开数学书，恰好翻到第16页”，这个事件是（）

A、随机事件 B、必然事件 C、不可能事件 D、确定事件

查看试题解析
5. 如图，河坝横断面迎水坡AB的坡比为1： $\sqrt{3}$ ，坝高BC＝3m，则AB的长度为（）

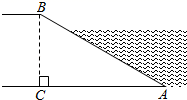A、6m B、3 $\sqrt{3}$ m C、9m D、6 $\sqrt{3}$ m

查看试题解析
6. 在一张缩印出来的纸上，一个三角形的一条边由原图中的6cm变成了2cm，则缩印出的三角形的面积是原图中三角形面积的（）

A、 $\frac{1}{3}$ B、 $\frac{1}{6}$ C、 $\frac{1}{9}$ D、 $\frac{1}{12}$

查看试题解析
7. 从前有一个醉汉拿着竹竿进城，横拿竖拿都进不去，横着比城门宽 $\frac{4}{3}$ 米，竖着比城门高 $\frac{2}{3}$ 米，一个聪明人告诉他沿着城门的两对角斜着拿竿，这个醉汉一试，不多不少刚好进去了，求竹竿的长度.若设竹竿长x米，则根据题意，可列方程（　　）

A、 ${(x + \frac{4}{3})}^{2} + {(x + \frac{2}{3})}^{2} = x^{2}$ B、 ${(x - \frac{4}{3})}^{2} + {(x - \frac{2}{3})}^{2} = x^{2}$ C、 ${(x - \frac{4}{3})}^{2} + {(x + \frac{2}{3})}^{2} = x^{2}$ D、 ${(x + \frac{4}{3})}^{2} + {(x - \frac{2}{3})}^{2} = x^{2}$

查看试题解析
8. 已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h＝－t²＋24t＋1.则下列说法中正确的是（）

A、点火后9 s和点火后13 s的升空高度相同 B、点火后24 s火箭落于地面 C、点火后10 s的升空高度为139 m D、火箭升空的最大高度为145 m

查看试题解析

二、填空题

9. 二次根式 $\sqrt{2 + x}$ 有意义，则x的取值范围是．

查看试题解析
10. 若关于x的一元二次方程 $x^{2} + 2 x - k = 0$ 的一个根为1，则k的值为．

查看试题解析
11. 如图，A ， B ， C是小正方形的顶点，且每个小正方形的边长为1，则cos∠BAC的值为．

查看试题解析
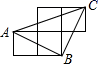12. 一个不透明的袋中装有除颜色外均相同的9个红球，3个白球，若干个绿球，每次摇匀后随机摸出一个球，记下颜色后再放回袋中，经过大量重复实验后，发现摸到绿球的概率稳定在0.2，则袋中有绿球个.

查看试题解析
13. 《九章算术》中记载了一种测量井深的方法．如图所示，在井口B处立一根垂直于井口的木杆BD ，从木杆的顶端D观察井水水岸C ，视线DC与井口的直径AB交于点E ，如果测得AB=1.8米，BD=1米，BE=0.2米，那么井深AC为米．

查看试题解析
14. 如图，在平面直角坐标系中，正方形 $O A B C$ 的顶点A在x轴正半轴上，顶点C在y轴正半轴上，抛物线 $y = a x^{2} - 2 a x + c$ 经过点B、C．若抛物线 $y = a x^{2} - 2 a x + c$ 的顶点在正方形 $O A B C$ 的内部，则a的取值范围是．

查看试题解析

三、解答题

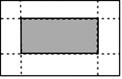
15. 计算： $(- \sqrt{2}) \times \sqrt{6} + \sqrt{15} \div \sqrt{5} + 2 \sin 60^{°}$

查看试题解析
16. 定义运算： $m * n = m n^{2} - m n - 3$ ，例如： $4 * 2 = 4 \times 2^{2} - 4 \times 2 - 3 = 5$ ．解方程： $1 * x = 0$ ．

查看试题解析
17. 某校七年级开展“经典诵读”比赛活动，诵读材料有《论语》、《三字经》、《弟子规》（分别用字母A、B、C依次表示这三个诵读材料），将A、B、C这三个字母分别写在3张完全相同的不透明卡片的正面上，把这3张卡片背面朝上洗匀后放在桌面上，小华和小敏参加诵读比赛，比赛时小华先从中随机抽取一张卡片，记录下卡片上的内容，放回后洗匀，再由小敏从中随机抽取一张卡片，选手按各自抽取的卡片上的内容进行诵读比赛，请用列表法或画树状图法求小华和小敏诵读两个不同材料的概率．

查看试题解析
18. 如图，在一个长10cm，宽6cm的矩形铁皮的四角各截去一个同样的小正方形，然后折叠成一个无盖的长方形盒子．若长方形盒子的底面（图中阴影部分）面积是32cm² ，求截去的小正方形的边长．

查看试题解析
19. 如图，某地修建高速公路，要从A地向B地修一座隧道（A、B在同一水平面上），为了测量A、B两地之间的距离，某工程师乘坐热气球从B地出发，垂直上升120米到达C处，在C处观察A地的俯角为42°，求A、B两地之间的距离．（结果精确到1米）（参考数据： $\sin 42^{°} = 0.67$ ， $\cos 42^{°} = 0.74$ ， $\tan 42^{°} = 0.90$ ）

查看试题解析
20. 以下各图均是由边长为1的小正方形组成的3×3网格， $△ A B C$ 的顶点均在格点上，利用网格和无刻度的直尺作图，保留痕迹，不写作法．

(1)、 $△$ ABC的面积为．

(2)、在图①中，作出 $△ A B C$ 的重心O．

(3)、在图②中，在 $△ A B C$ 的边AC上找一点F，连结BF，使 $△ A B F$ 的面积为 $\frac{4}{3}$ ．

查看试题解析
21. 某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处回合，如图所示，以水平方向为 $x$ 轴，喷水池中心为原点建立平面直角坐标系.

(1)、求水柱所在抛物线（第一象限部分）的函数表达式；

(2)、王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？

查看试题解析
22. 在矩形 $A B C D$ 中，E为边 $C D$ 上一点，把 $△ A D E$ 沿 $A E$ 翻折，使点D恰好落在边 $B C$ 上的点F处．

(1)、求证： $△ A B F ∽ △ F C E$ ．

(2)、若 $A D = 10$ ， $C D = 6$ ，则 $\tan ∠ E A F$ 的值为．

(3)、若 $A D = 6$ ， $D E = 3$ ，则AB的长为．

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90^{°}$ ， $A B = 3$ ， $B C = 4$ ，动点P从点A出发，沿AC方向以每秒1个单位长度的速度向终点C运动，将线段AP绕点P逆时针旋转90°，得到线段PQ，过点Q作 $Q M ⊥ A B$ ，交射线AC于点M．设点P的运动时间为t秒．

(1)、线段MP的长为（用含t的代数式表示）．

(2)、当点M与点C重合时，求t的值．

(3)、设 $△ P Q M$ 与 $△ A B C$ 重叠部分图形的面积为S（ $S > 0$ ），求S与t之间的函数关系式．

(4)、取线段PM的中点H，作直线BH，当直线BH将 $△ P Q M$ 分成的两部分图形的面积比为1：3时，直接写出此时t的值．

查看试题解析
24. 在平面直角坐标系中，函数 $y = - x^{2} + 2 m x - 2 m (x ⩽ 2)$ 的图象记为 $G_{1}$ ．

(1)、图象 $G_{1}$ 过定点．

(2)、若图象 $G_{1}$ 的最高点到x轴的距离为1，求此时m的值．

(3)、将图象 $G_{1}$ 沿直线 $x = 2$ 翻折，翻折后的图象记为 $G_{2}$ ， $G_{1}$ 和 $G_{2}$ 合称为图象G．
①当 $m = 0$ 时，在如图的平面直角坐标系中画出图象G．

②点 $A (m - 1 ， - 1)$ 、 $B (m + 1 ， - 1)$ ，当图象G和线段AB有且只有两个公共点时，直接写出m的取值范围．

查看试题解析