吉林省四平市公主岭市2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} - 3 x - 1 = 0$ 的根的情况为（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
2. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 将抛物线 $y = x^{2}$ 向下平移3个单位长度，得到的抛物线的函数解析式为（）

A、 $y = x^{2} - 3$ B、 $y = x^{2} + 3$ C、 $y = {(x - 3)}^{2}$ D、 $y = {(x + 3)}^{2}$

查看试题解析
4. 在一个不透明的盒子中装有n个小球，它们除了颜色不同外，其余都相同，其中有4个白球，每次试验前，将盒子中的小球摇匀，随机摸出一个球记下颜色后再放回盒中．大量重复上述试验后发现，摸到白球的频率稳定在0.4，那么可以推算出n大约是（　　）

A、10 B、14 C、16 D、40

查看试题解析
5. 如图，点A是反比例函数 $y = - \frac{4}{x}$ 图象上的一个动点，过点A作AB⊥x轴，AC⊥y轴，垂足分别为B ， C ，则矩形ABOC的面积为（）

A、-4 B、2 C、4 D、8

查看试题解析
6. 如图，AB是⊙O的弦（AB不是直径），以点A为圆心，以AB长为半径画弧交⊙O于点C，连结AC、BC、OB、OC．若∠ABC=65°，则∠BOC的度数是（）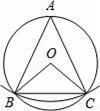

A、50° B、65° C、100° D、130°

查看试题解析

二、填空题

7. 在平面直角坐标系中，点（﹣3，2）关于原点对称的点的坐标是

查看试题解析
8. 已知 $x = - 1$ 是方程 $x^{2} - a = 0$ 的解，则 $a =$ ．

查看试题解析
9. 已知一个反比例函数的图象经过点P（3，4），请你写出该反比例函数图象上异于点P的另外一个点的坐标(写出一个即可）．

查看试题解析
10. 如图，点（1，0），（0，3）在抛物线y=-x²+bx+c上，且抛物线的对称轴为x=-1，若y＞0，则x的取值范围是．

查看试题解析
11. 如图，一个可以自由转动的转盘被等分成8个扇形区域，并涂上了相应的颜色，转动转盘，转盘停止后，指针指向黄色区域的概率是．

查看试题解析
12. 如图，将一个直角三角板ACB（∠C=90°）绕60°角的顶点B顺时针旋转，使得点C旋转到AB的延长线上的点E处，则三角板旋转了度．

查看试题解析
13. 如图，⊙O的半径OC=10cm ，直线l⊥OC ，垂足为H ，且l交⊙O于A ， B两点，AB=16cm ，则l沿OC所在直线向下平移cm时与⊙O相切．

查看试题解析
14. 如图，点A（m，2），B（5，n）在函数 $y = \frac{k}{x}$ （k＞0，x＞0）的图象上，将该函数图象向上平移2个单位长度得到一条新的曲线，点A、B的对应点分别为A′、B′．图中阴影部分的面积为8，则k的值为．

查看试题解析
15. 如图，点A（x₁ ， y₁），B（x₂ ， y₂)在反比例函数 $y = \frac{5}{x}$ （x＞0）的图象上，且x₁＜x₂ ．

(1)、请比较y₁ ， y₂的大小：y₁ y₂（填“＞”，“＜”或“=”）．

(2)、若点A关于y轴对称的对称点 $A^{'}$ 在反比例函数 $y = \frac{k}{x}$ （k≠0）的图象上，则k的值为．

查看试题解析

三、解答题

16. 解方程：x²﹣3x+1＝0．

查看试题解析
17. 如图①，在 $4 \times 8$ 的网格中，每个小正方形的边长都为1，点A ， B ， C ， P都在格点上，按图②的程序移动点P ．

(1)、请在图①中画出点P所经过的路径．

(2)、点P经过的路径的总长为（结果保留 $π$ ）．

查看试题解析
18. 如图，⊙O交x轴于A ， B两点，交y轴的正半轴于点C ，点D为第一象限内⊙O上的一点，连接AD ， OD ， CD ，已知∠DAB = 15°，CD=2．

(1)、∠OCD =度．

(2)、 $S_{扇形 O C D}$ = ．

查看试题解析
19. 如图，利用一面墙（墙的长度为20米），用34米长的篱笆围成两个鸡场．中间用一道篱笆隔开，每个鸡场均留一道1米宽的门，若两个鸡场总面积为96平方米，求AB的长．

查看试题解析
20. 某中学食堂在某天早餐提供了A（猪肉包），B（鸡蛋），C（油饼）三样食品，为了便于学生尽快就餐，师生约定：早餐每人一份，每份含有两样不同的食品各一个，食堂师傅在窗口随机发放．

(1)、按约定，“小李同学在该天早餐得到两个油饼”是事件（填“可能”“必然”或“不可能”）．

(2)、请用列表或画树状图的方法，求出小张同学该天早餐刚好得到A（猪肉包）和C（油饼）的概率．

查看试题解析
21. 如图，在△ABC中，AB=AC ，以AB为直径的⊙O交BC于点D ，过点D作DE⊥AC于点E ．

(1)、求证：DE是⊙O的切线．

(2)、若∠B=30°，AB=8，求BD的长．

查看试题解析
22. 如图，在矩形OABC中，OA=3，OC=2，点F在AB上（点F不与点A ， B重合），OA ， OC分别在x轴，y轴上，过点F的反比例函数 $y = \frac{k}{x}$ （k＞0）的图象与BC边交于点E ．

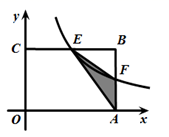(1)、点E的坐标为，点F的坐标为（用含k的式子表示）．

(2)、求k为何值时，△EFA的面积最大，最大面积是多少？

查看试题解析
23. 如图，有一座抛物线形拱桥，在正常水位时水面AB的宽为20米，如果水位上升3米，则水面CD的宽是10米．

(1)、建立如图所示的直角坐标系，求此抛物线的解析式；

(2)、当水位在正常水位时，有一艘宽为6米的货船经过这里，船舱上有高出水面3.6米的长方体货物（货物与货船同宽）．问：此船能否顺利通过这座拱桥？

查看试题解析
24. 如图①，点O为正方形ABCD的中心，分别延长OA ， OD到点F ， E ，使OF=2OA ， OE=2OD ，连接EF ．将△EOF绕点O逆时针旋转 $α$ 得到△E₁OF₁（如图②），连接AE₁ ， BF₁ ．

(1)、探究AE₁与BF₁的数量关系，并给予证明．

(2)、当OA⊥AE₁时， $α$ =度．

查看试题解析
25. 如图，在Rt△ABC中，∠C=90°，∠A=45°，AC= $2 \sqrt{2}$ ．动点P从点A出发，沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D（点P不与点A ， B重合），作∠DPQ=45°，边PQ交射线DC于点Q ．设点P的运动时间为t秒．

(1)、线段DC的长为（用含t的式子表示）．

(2)、当点Q与点C重合时，求t的值．

(3)、设△PDQ与△ABC重叠部分的面积为S ，求S与t之间的函数关系式．

查看试题解析
26. 如图，抛物线y=ax²+bx+3（a≠0）与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C ，过点C作CD∥x轴交抛物线于点D ，连接BC ， BD ．

(1)、a= ， b= ．

(2)、点D的坐标为；直线BC的函数解析式为；直线BD的函数解析式为．

(3)、将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移，当点O与点B重合时，△BOC停止运动，记平移后的三角形为△B′O′C′ ．在平移过程中，△B′O′C′ 与△BCD重叠的面积记为S ，设平移的时间为t秒，试求S与t之间的函数关系式．

查看试题解析