吉林省吉林市舒兰市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-23 类型:期末考试
一、单选题
-
1. 下列方程中,关于x的一元二次方程是( )A、x2+x+y=0 B、(x+3)2=x2+2x C、 D、 x2﹣3x+1=02. 如图,△ABC内接于⊙O,若 ∠AOB=100° ,则∠ACB的度数是( )
 A、40° B、50° C、60° D、80°3. 下列图形中,是中心对称但不是轴对称图形的为( )A、
A、40° B、50° C、60° D、80°3. 下列图形中,是中心对称但不是轴对称图形的为( )A、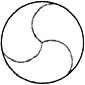 B、
B、 C、
C、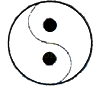 D、
D、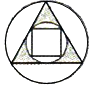 4. 下列函数中,当x﹥0时,y随x的增大而减小的是:A、y=x+1 B、 C、 D、5. 函数y=mx2+(m+2)x+ m+1的图象与x轴只有一个交点,则m的值为( )A、0 B、0或2 C、0或2或﹣2 D、2或﹣26. 如图,是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①b2>4ac;②2a+b=0;③若点B(﹣ ,y1)、C(﹣ ,y2)为函数图象上的两点,则y1<y2;④a+b+c>0,其中正确结论是 ( )
4. 下列函数中,当x﹥0时,y随x的增大而减小的是:A、y=x+1 B、 C、 D、5. 函数y=mx2+(m+2)x+ m+1的图象与x轴只有一个交点,则m的值为( )A、0 B、0或2 C、0或2或﹣2 D、2或﹣26. 如图,是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①b2>4ac;②2a+b=0;③若点B(﹣ ,y1)、C(﹣ ,y2)为函数图象上的两点,则y1<y2;④a+b+c>0,其中正确结论是 ( ) A、①③ B、②③ C、①④ D、②④
A、①③ B、②③ C、①④ D、②④二、填空题
-
7. 如果从长度分别为2、4、6、7的四条线段中随机抽取三条线段,那么抽取的三条线段能构成三角形的概率是 .8. 若 ,且一元二次方程 有实数根,则 的取值范围是.9. 已知圆锥的底面半径为5,母线长为13,则这个圆锥的侧面积是 .10. 将抛物线: 向下平移3个单位,再向右平移4个单位得到的抛物线是.11. 已知正比例函数 与反比例函数 的图象的一个交点坐标为(-1,2),则另一个交点的坐标为
12. 如图,原点O为平行四边形A.BCD的对角线A.C的中点,顶点A,B,C,D的坐标分别为(4,2),( ,b),(m,n),(-3,2).则(m+n)( +b)= . 13. 如图,点A在双曲线 上,AB⊥x轴于B,且△AOB的面积S△AOB=2,则k= .
13. 如图,点A在双曲线 上,AB⊥x轴于B,且△AOB的面积S△AOB=2,则k= . 14. 如图,在平面直角坐标系中,抛物线y=x2+mx交x轴的负半轴于点A.点B是y轴正半轴上一点,点A关于点B的对称点A′恰好落在抛物线上.过点A′作x轴的平行线交抛物线于另一点C.若点A′的横坐标为1,则A′C的长为 .
14. 如图,在平面直角坐标系中,抛物线y=x2+mx交x轴的负半轴于点A.点B是y轴正半轴上一点,点A关于点B的对称点A′恰好落在抛物线上.过点A′作x轴的平行线交抛物线于另一点C.若点A′的横坐标为1,则A′C的长为 .
三、解答题
-
15. 解方程:x(x﹣2)+x﹣2=0.16. 已知抛物线y=-x2+bx+c与直线y=-4x+m相交于第一象限内不同的两点A(5,n),B(3,9),求此抛物线的解析式.17. 如图,△ABC的直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,求PP′的长.
 18. 如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切于点C时,另一边与圆两个交点A和B的读数恰好为“2”和“8”(单位:cm)求该圆的半径.
18. 如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切于点C时,另一边与圆两个交点A和B的读数恰好为“2”和“8”(单位:cm)求该圆的半径. 19. 如图,有甲、乙两个转盘,每个转盘上各个扇形的圆心角都相等,让两个转盘分别自由转动一次,当转盘指针落在分界线上时,重新转动.
19. 如图,有甲、乙两个转盘,每个转盘上各个扇形的圆心角都相等,让两个转盘分别自由转动一次,当转盘指针落在分界线上时,重新转动.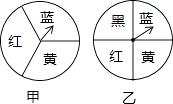 (1)、请你画树状图或列表表示所有等可能的结果.(2)、求两个指针落在区域的颜色能配成绿色的概率.(黄、蓝两色混合配成绿色)20. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)、请你画树状图或列表表示所有等可能的结果.(2)、求两个指针落在区域的颜色能配成绿色的概率.(黄、蓝两色混合配成绿色)20. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度). (1)、①画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是 ▲ ;
(1)、①画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是 ▲ ;②以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ▲ ;
(2)、△A2B2C2的面积是平方单位.21. 某水果批发商场经销一种水果,如果每千克盈利10元,每天可售出400千克.经市场调查 现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.(1)、若商场只要求保证每天的盈利为4420元,同时又可使顾客得到实惠,每千克应涨价为多少元?(2)、当每千克涨价为多少元时,每天的盈利最多?最多是多少?22. 如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠B. (1)、求证:直线AE是⊙O的切线;(2)、若∠D=60°,AB=6时,求劣弧 的长(结果保留π).23. 如图,已知反比例函数y= 与一次函数y=x+b的图象在第一象限相交于点A(3,﹣k+4)
(1)、求证:直线AE是⊙O的切线;(2)、若∠D=60°,AB=6时,求劣弧 的长(结果保留π).23. 如图,已知反比例函数y= 与一次函数y=x+b的图象在第一象限相交于点A(3,﹣k+4) (1)、试确定这两个函数的表达式;(2)、求出这两个函数图象的另一个交点B的坐标,并根据图象写出使一次函数的值小于反比例函数值的x的取值范围.24. 如图,在平行四边形 中, 是 的延长线上一点, 与 交于点 .
(1)、试确定这两个函数的表达式;(2)、求出这两个函数图象的另一个交点B的坐标,并根据图象写出使一次函数的值小于反比例函数值的x的取值范围.24. 如图,在平行四边形 中, 是 的延长线上一点, 与 交于点 .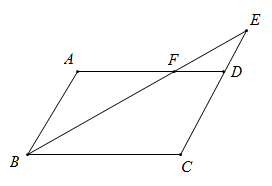 (1)、求证:(2)、若 的面积为 ,求平行四边形 的面积25. 如图,在△ABC中,AB=AC=5,BC=6,点D为AB边上的一动点(D不与A、B重合),过D作DE∥BC , 交AC于点E . 把△ADE沿直线DE折叠,点A落在点A'处.连结BA',设AD=x , △ADE的边DE上的高为y .
(1)、求证:(2)、若 的面积为 ,求平行四边形 的面积25. 如图,在△ABC中,AB=AC=5,BC=6,点D为AB边上的一动点(D不与A、B重合),过D作DE∥BC , 交AC于点E . 把△ADE沿直线DE折叠,点A落在点A'处.连结BA',设AD=x , △ADE的边DE上的高为y . (1)、求出y与x的函数关系式;(2)、若以点A'、B、D为顶点的三角形与△ABC 相似,求x的值;(3)、当x取何值时,△A' DB是直角三角形.26. 如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.
(1)、求出y与x的函数关系式;(2)、若以点A'、B、D为顶点的三角形与△ABC 相似,求x的值;(3)、当x取何值时,△A' DB是直角三角形.26. 如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.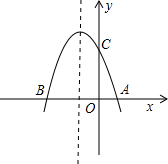 (1)、求该抛物线的解析式;(2)、设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;(3)、在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
(1)、求该抛物线的解析式;(2)、设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;(3)、在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.