广东省广州市天河区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列选项的汽车标志图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. “购买1张彩票，中奖”这个事件是（）

A、不可能事件 B、必然事件 C、确定性事件 D、随机事件

查看试题解析
3. 函数 $y = {(x - 4)}^{2} + 5$ 的顶点坐标为（）

A、 $(- 4 ， 5)$ B、 $(4 ， 5)$ C、 $(4 ， - 5)$ D、 $(- 4 ， - 5)$

查看试题解析
4. 点 $(1 ， - 1)$ 关于原点对称的点的坐标为（）

A、 $(1 ， 1)$ B、 $(1 ， - 1)$ C、(-1，-1) D、 $(- 1 ， 1)$

查看试题解析
5. 一元二次方程 $x^{2} - 4 x + 4 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
6. 若四边形 $A B C D$ 是 $⊙ O$ 的内接四边形，且 $∠ A B C = 60 °$ ，则 $∠ A D C$ 的度数为（）

A、 $60 °$ B、 $120 °$ C、 $150 °$ D、 $30 °$

查看试题解析
7. 在英语单词 $r o t a t i o n$ （旋转）中任意选择一个字母，字母为“ $t$ ”的概率与字母为“ $o$ ”的概率之和为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{4}$ C、 $\frac{3}{8}$ D、 $\frac{1}{2}$

查看试题解析
8. 一个圆的半径为 $4$ ，则该圆的内接正方形的边长为（）

A、 $2 \sqrt{2}$ B、 $3 \sqrt{2}$ C、 $4 \sqrt{2}$ D、 $5 \sqrt{2}$

查看试题解析
9. 2017﹣2018赛季中国男子篮球职业联赛，采用双循环制（每两队之间都进行两场比赛），比赛总场数为380场，若设参赛队伍有x支，则可列方程为（　　）

A、 $\frac{1}{2} x (x - 1) = 380$ B、 $x (x - 1) = 380$ C、 $\frac{1}{2} x (x + 1) = 380$ D、 $x (x + 1) = 380$

查看试题解析
10. 二次函数y=ax²+bx+c（a≠0）的图象如图所示，下列结论：①ac＞0；②当x≥1时，y随x的增大而减小；③2a+b=0；④b²-4ac＜0；⑤4a-2b+c＞0，其中正确的个数是（）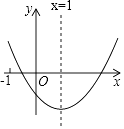

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 方程 $x^{2} - 2 x - 3 = 0$ 的解是．

查看试题解析
12. 如图， $E$ 是正方形 $A B C D$ 中 $C D$ 边上的中点， $A B = 4$ ，把 $Δ A D E$ 绕点 $A$ 顺时针旋转 $90 °$ 得到 $Δ A B F$ ，若连接 $E F$ ，则 $E F =$ ．

查看试题解析
13. 在一个不透明的袋子里装有红球、黄球共20个，这些球除颜色外都相同．小明通过多次实验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数最有可能的是．

查看试题解析
14. 若x=1是关于x的一元二次方程x²+3mx+n=0的解，则6m+2n= ．

查看试题解析
15. $Rt Δ A B C$ 中， $∠ A B C = 90 °$ ， $A B = 3$ ， $B C = 4$ ，将 $Δ A B C$ 沿 $A C$ 所在直线旋转一周，所得几何体的全面积是．（结果保留 $π$ ）

查看试题解析
16. 已知 $⊙ O$ 的半径为 $10 c m$ ， $A B$ ， $C D$ 是 $⊙ O$ 的两条弦， $A B / / C D$ ， $A B = 16 c m$ ， $C D = 12 c m$ ，则弦 $A B$ 和 $C D$ 之间的距离是 $c m$ ．

查看试题解析

三、解答题

17. 解方程： $6 x^{2} - 2 x - 1 = 2 x^{2} - 2 x$ ．

查看试题解析
18. 如图， $D$ 是 $Δ A B C$ 的边 $B C$ 延长线上一点，连接 $A D$ ，把 $Δ A C D$ 绕点 $A$ 顺时针旋转 $60 °$ 恰好得到 $Δ A B E$ ，其中 $D$ ， $E$ 是对应点，若 $∠ C A D = 18 °$ ，求 $∠ E A C$ 的度数．

查看试题解析
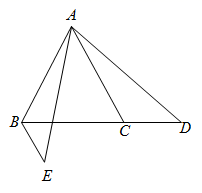19. 某商场某型号的计算机2018年销售量为 $2880$ 台，2020年受疫情影响，年销售量下降为 $2000$ 台，求销售量的年平均下降率．（结果保留整数）

查看试题解析
20. 经过某路口的汽车只能向左转或者向右转，如果两种可能性相同，现有两辆汽车经过这个路口，请用列举法求事件“一辆汽车向左转，一辆汽车向右转”的概率．

查看试题解析
21. 如图，已知△ABC ， ∠B=40°，AB=AC ．

(1)、尺规作图：作⊙O ，使它经过A ， B ， C三点；

(2)、在（1）中所作的⊙O中，∠ACB的平分线CD交⊙O于点D ，连接OD ， OC ，求∠DOC的度数．

查看试题解析
22. 如图，在正方形 $A B C D$ 中，分别以 $B ， D$ 为圆心，以正方形的边长 $2$ 为半径画弧，形成阴影部分的树叶图案（计算时 $π$ 取 $3$ ）．

(1)、求 $\overset{⌢}{A C}$ 的长和阴影部分的面积；

(2)、若在正方形 $A B C D$ 中随机撒一粒豆子，求豆子落在阴影区域内的概率（豆子落在弧上不计）

查看试题解析
23. 在平面直角坐标系中，已知点 $A$ 的坐标为 $(0 ， 1)$ ，点 $M$ 是 $x$ 轴上的一个动点．连接 $A M$ ，过点 $M$ 作 $y$ 轴的平行线交线段 $A M$ 的垂直平分线于点 $P (x ， y)$ ．

(1)、求 $y$ 关于 $x$ 的函数关系式；

(2)、在（1）中，若求得的函数图象是直线，请求出它与直线 $y = x + 1$ 、坐标轴围成的图形面积；若是抛物线，设它与直线 $y = x + 1$ 交于点 $B$ ， $C$ ，顶点为 $Q$ ，求 $Δ Q B C$ 的面积．

查看试题解析
24. 如图， $A D$ ， $B C$ ， $C D$ 分别与 $⊙ O$ 相切于 $A$ ， $B$ ， $E$ 三点， $A B$ 是 $⊙ O$ 的直径．

(1)、连接 $O C$ ， $O D$ ，若 $O C = 4$ ， $O D = 3$ ，求 $C D$ 的长；

(2)、若 $A D = x$ ， $B C = y$ ， $A B = 4$ ，请画出 $y$ 关于 $x$ 的函数图象．

查看试题解析
25. 对于实数 $a$ 和 $b$ ，定义新运算“ $\otimes$ ”： $a \otimes b = {\begin{array}{l} a + b ，当 a \leq b 时； \\ a - b ，当 a > b 时 . \end{array}$

(1)、若 $(2 x - 1) \otimes (3 - 2 x) = x^{2}$ ，求实数 $x$ 的值；

(2)、设函数 $y_{1} = (2 - x^{2}) \otimes (4 x - x^{2})$ ，若函数 $y_{2} = y_{1} - m$ 的图象与坐标轴恰有两个交点，求实数 $m$ 的取值范围．

查看试题解析