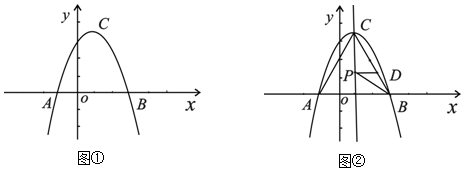广东省珠海市香洲区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-23 类型:期末考试
一、单选题
-
1. 下列数学符号中,不是中心对称图形的是( )A、∽ B、// C、> D、=2. 下列事件中是必然事件的是( )A、明天太阳从东方升起 B、投掷一枚均匀的硬币 次,正面朝上的次数为 次 C、射击运动员射击一次,命中靶心 D、平面内,任意一个五边形的外角和等于3. 平面内,已知 的半径为 ,则点 与 的位置关系是( )A、点 在 上 B、点 在 内 C、点 在 外 D、不能确定4. 抛物线 的顶点坐标是( )A、 B、 C、 D、5. 一枚飞任意投掷到如图所示的同心圆镖盘上,此镖盘上有两个同心圆,三条直径把大圆分成六等份,飞镖落在白色区域的概率为( )
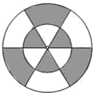 A、 B、 C、 D、6. 抛物线 向左平移5个单位,再向下平移1个单位,所得到的抛物线是( )A、 B、 C、 D、7. 在元旦庆祝活动中,参加活动的同学互赠贺卡,共送贺卡42张,设参加活动的同学有 人,根据题意,可列方程( )A、 B、 C、 D、8. 已知反比例函数 ,下列结论错误的是( )A、其图象经过点 B、其图象位于第二、第四象限 C、当 时, 随 的增大而增大 D、当 时,9. 如图,将 绕顶点 旋转得到 ,点 对应点 ,点 对应点 ,点 刚好落在 边上, ,则 等于( )
A、 B、 C、 D、6. 抛物线 向左平移5个单位,再向下平移1个单位,所得到的抛物线是( )A、 B、 C、 D、7. 在元旦庆祝活动中,参加活动的同学互赠贺卡,共送贺卡42张,设参加活动的同学有 人,根据题意,可列方程( )A、 B、 C、 D、8. 已知反比例函数 ,下列结论错误的是( )A、其图象经过点 B、其图象位于第二、第四象限 C、当 时, 随 的增大而增大 D、当 时,9. 如图,将 绕顶点 旋转得到 ,点 对应点 ,点 对应点 ,点 刚好落在 边上, ,则 等于( ) A、 B、 C、 D、10. 如图,已知二次函数 的图象与 轴交于点 ,对称轴为直线 ,下列结论:① ;② ;③ ;④ ( 是任意实数),其中正确的是( )
A、 B、 C、 D、10. 如图,已知二次函数 的图象与 轴交于点 ,对称轴为直线 ,下列结论:① ;② ;③ ;④ ( 是任意实数),其中正确的是( ) A、①② B、②③ C、①②③ D、②③④
A、①② B、②③ C、①②③ D、②③④二、填空题
-
11. 一个事件经过多次试验,某种结果发生的频率为0.31,那么估计该种结果发生的概率是 .12. 若正方体的棱长为 ,表面积为 ,则 与 的关系式为 .13. 如果关于x的一元二次方程 的一个解是 ,则 .14. 如图,圆锥的母线长 为 ,底面圆半径 为 ,则该圆锥的侧面积为 .
 15. 关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是 .16. 如图,在反比例函数 和 的图象上取 两点,若 轴, 的面积为 ,则 .
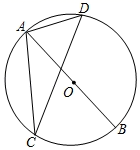
15. 关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是 .16. 如图,在反比例函数 和 的图象上取 两点,若 轴, 的面积为 ,则 . 17. 如图,已知 为 直径,若 是 内接正 边形的一边, 是 内接正 边形的一边, ,则 .
17. 如图,已知 为 直径,若 是 内接正 边形的一边, 是 内接正 边形的一边, ,则 .
三、解答题
-
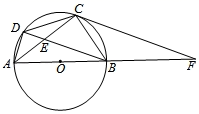
18. 解方程:x2-4x+1=0(配方法)19. 如图, 是 直径, 是 的弦, ,求 的度数.
 20. 为响应垃圾分类处理、改善生态环境的号召,某小区将生活垃圾分成四类,并设置了相应的四个垃圾箱, :可回收物垃圾箱, :有害垃圾箱, :餐厨垃圾箱, :其它垃圾箱.甲、乙两人分别投放了一袋垃圾,请用列表或画树状图的方法求甲、乙投放到不同垃圾箱的概率.21. 在如图所示的网格中,每个小正方形的边长为 ,将 绕着点 顺时针旋转 ,得到 .
20. 为响应垃圾分类处理、改善生态环境的号召,某小区将生活垃圾分成四类,并设置了相应的四个垃圾箱, :可回收物垃圾箱, :有害垃圾箱, :餐厨垃圾箱, :其它垃圾箱.甲、乙两人分别投放了一袋垃圾,请用列表或画树状图的方法求甲、乙投放到不同垃圾箱的概率.21. 在如图所示的网格中,每个小正方形的边长为 ,将 绕着点 顺时针旋转 ,得到 .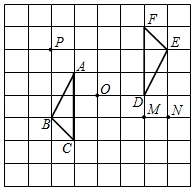 (1)、画出 ;(2)、求点 在旋转过程中的路径长;(3)、 可以看作是由 旋转得到,在点 中,点是旋转中心.22. 劳动是财富的源泉,也是幸福的源泉.某中学对劳动教育进行积极探索和实践,创建学生劳动教育地,让学生参与到农耕劳作中.如图,现准备利用校园围墙的一段 ( 最长可用 ),用 长的篱笆,围成一个矩形菜园 .
(1)、画出 ;(2)、求点 在旋转过程中的路径长;(3)、 可以看作是由 旋转得到,在点 中,点是旋转中心.22. 劳动是财富的源泉,也是幸福的源泉.某中学对劳动教育进行积极探索和实践,创建学生劳动教育地,让学生参与到农耕劳作中.如图,现准备利用校园围墙的一段 ( 最长可用 ),用 长的篱笆,围成一个矩形菜园 . (1)、当AB长度为多少时,矩形菜园的面积为 ?(2)、能否围成面积为 的矩形菜园?为什么?23. 如图,在平面直角坐标系中,点 ,把线段 绕点 逆时针旋转 到 , 交 轴于点 ,反比例函数 的图象经过点 .
(1)、当AB长度为多少时,矩形菜园的面积为 ?(2)、能否围成面积为 的矩形菜园?为什么?23. 如图,在平面直角坐标系中,点 ,把线段 绕点 逆时针旋转 到 , 交 轴于点 ,反比例函数 的图象经过点 . (1)、求 的值;(2)、连接 ,若点 在反比例函数 的图象上,且 ,求点 的坐标.
(1)、求 的值;(2)、连接 ,若点 在反比例函数 的图象上,且 ,求点 的坐标.