广东省珠海市斗门区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个图形中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 抛物线y=（x﹣2）²+3的顶点坐标是（）

A、（2，3） B、（﹣2，3） C、（2，﹣3） D、（﹣2，﹣3）

查看试题解析
3. 下列事件中，是必然事件的是（）

A、通常加热到100°C时，水沸腾 B、掷一次骰子，向上一面的点数是6 C、经过有交通信号灯的路口，遇到红灯 D、射击运动员射击次，命中靶心

查看试题解析
4. 下面四个关系式中，y是x的反比例函数的是（）

A、 $y = \frac{x}{2}$ B、 $y = \frac{\sqrt{5}}{3 x}$ C、y＝x² D、y＝ $\frac{2}{x + 1}$

查看试题解析
5. 将半径为6的半圆形纸片围成一个圆锥，那么这个圆锥的侧面积等于（）

A、6π B、18π C、36π D、72π

查看试题解析
6. 用配方法解方程x²＋1=8x，变形后的结果正确的是(　　)

A、(x＋4)²=15 B、(x＋4)²=17 C、(x－4)²=15 D、(x－4)²=17

查看试题解析
7. 已知正六边形的边长为4，则这个正六边形外接圆的半径为（）

A、2 B、2 $\sqrt{3}$ C、4 D、4 $\sqrt{3}$

查看试题解析
8. 若关于x的一元二次方程x²＋x﹣m＝0有实数根，则m的取值范围是（）

A、 $m > \frac{1}{4}$ B、 $m \geq - \frac{1}{4}$ C、 $m \leq \frac{1}{4}$ D、 $m \leq - \frac{1}{4}$

查看试题解析

二、填空题

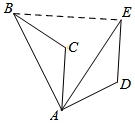
9. 一元二次方程x（x+3）=0的根是．

查看试题解析
10. 在平面直角坐标系中，点（﹣3，4）关于原点对称的点的坐标是．

查看试题解析
11. 在半径为6cm的圆中，50°的圆心角所对的弧长为cm．

查看试题解析
12. 如图，将△ABC绕点A顺时针旋转60°得到△AED ．若线段AB＝3，则△ABE的周长等于．

查看试题解析
13. 一定质量的氧气，它的密度ρ（kg/m³）是它的体积V（m³）的反比例函数，当V＝100m³时，ρ＝1.4kg/m³；那么当V＝2m³时，氧气的密度为kg/m^3.

查看试题解析
14. 在一个不透明的盒子中装有2个白球，n个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，它是黄球的概率为 $\frac{2}{3}$ ，则n= ．

查看试题解析
15. 如图是足球守门员在O处开出一记手抛高球后足球在空中运动到落地的过程，它是一条经过A、M、C三点的抛物线．其中A点离地面1.4米，M点是足球运动过程中的最高点，离地面3.2米，离守门员的水平距离为6米，点C是球落地时的第一点．那么足球第一次落地点C距守门员的水平距离为米．

查看试题解析

三、解答题

16. 二次函数y＝x²﹣2x﹣3的图象与x轴交于A、B两点，已知点A在点B的左侧，求点A和点B的坐标．

查看试题解析
17. 在校园文化艺术节中，九年级班有1名男生和2名女生获得美术奖，另有1名男生和1名女生获得音乐奖，分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会，利用列表法或树状图求刚好是2名女生参加颁奖大会的概率．

查看试题解析
18. 假设某地有一个人患了新型冠状病毒，经过两轮传染后共有169人患了此病毒．

(1)、求每轮传染中平均一个人传染了几个人？

(2)、按照这样的速度传染，三轮传染后共有多少人患了新型冠状病毒？

查看试题解析
19. 如图，点O是坐标原点，△OBA∽△DOC ，边OA、OC都在x轴的正半轴上．已知点B的坐标为（12，16），∠BAO＝∠OCD＝90°，OD＝10，反比例函数的图象经过点D ，交AB边于点E ．

(1)、求该反比例函数的解析式；

(2)、求BE的长．

查看试题解析
20. 如图1，在 $Δ A B C$ 中， $B A = B C$ ， $D$ ， $E$ 是 $A C$ 边上的两点，且满足 $∠ D B E = \frac{1}{2} ∠ A B C (0 ° < ∠ C B E < \frac{1}{2} ∠ A B C)$ ．以点 $B$ 为旋转中心，将 $Δ B E C$ 按逆时针旋转 $∠ A B C$ ，得到△ $B E^{'} A$ （点 $C$ 与点 $A$ 重合，点 $E$ 到点 $E^{'}$ 处）连接 $D E^{'}$ ．

(1)、求证： $D E^{'} = D E$ ；

(2)、如图2，若AB⊥BC ，其他条件不变．求证：DE²＝AD²＋EC^2.

查看试题解析
21. 如图，AB是⊙O的直径，C、D是⊙O上两点．AE与过点C的切线垂直，垂足为E ，直线EC与直径AB的延长线相交于点P ，弦CD交AB于点F ，连接AC、AD、BC、BD ．

(1)、若∠ABC＝∠ABD＝60°，判断△ACD的形状，并证明你的结论；

(2)、若CD平分∠ACB ，求证：PC＝PF；

(3)、在（2）的条件下，若AD＝5 $\sqrt{2}$ ，PF＝5 $\sqrt{3}$ ，求由线段PC、 $\overset{⌢}{C B}$ 和线段BP所围成的图形（阴影部分）的面积．

查看试题解析
22. 如图1，在矩形ABOC中，OB＝4，OC＝3，以顶点O为坐标原点，OB、OC所在的直线为坐标轴建立直角坐标系．点D与点B关于原点对称，连接BC、CD ，点M以每秒2个单位长度的速度沿B→C→D运动（M不与点B、D重合），设运动时间为t（秒）．

(1)、求经过A、C、D三点的抛物线的解析式；

(2)、当M为BC的中点时，在抛物线上是否存在一点P ，使△PAM≌△PBM？若存在，求出点P的坐标；若不存在，请说明理由．

(3)、当点M在CD上运动时，如图2，过点M作ME⊥AB、MF⊥x轴，垂足为E、F ，线段ME与y轴交于点G、与线段BC交于点H ．设矩形BEMF与△BCD重叠部分的面积为S ，求S与t的函数关系式，并求出S的最大值．

查看试题解析