广东省汕尾市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-23 类型:期末考试
一、单选题
-
1. 一5的绝对值是( )A、5 B、 C、 D、-52. 在抗击“新冠”疫情的战斗中,汕尾地区医务人员在短短3天内,就完成了人员及环境样本83400份的采样与检测工作.将83400用科学记数法表示为( )A、 B、 C、 D、3. 下列图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 若式子 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、5. 如图,过 上一点 作 的切线,交 直径 的延长线于点 ,连接 .若 ,则 的度数为( )
4. 若式子 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、5. 如图,过 上一点 作 的切线,交 直径 的延长线于点 ,连接 .若 ,则 的度数为( ) A、 B、 C、 D、6. 水平放置的圆柱形排水管道截面半径为1 m.若管道中积水最深处为0.4 m,则水面宽度为( )
A、 B、 C、 D、6. 水平放置的圆柱形排水管道截面半径为1 m.若管道中积水最深处为0.4 m,则水面宽度为( ) A、0.8 m B、1.2 m C、1.6 m D、1.8 m7. 若关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是( ).A、 且 B、 且 C、 D、8. 如图,直线 经过点 , ,则不等式 的解集是( )
A、0.8 m B、1.2 m C、1.6 m D、1.8 m7. 若关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是( ).A、 且 B、 且 C、 D、8. 如图,直线 经过点 , ,则不等式 的解集是( ) A、 B、 C、 D、9. 如图,将矩形纸片 折叠,使点 与点 重合,折痕为 .若 , ,那么线段 的长为( )
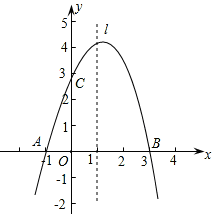
A、 B、 C、 D、9. 如图,将矩形纸片 折叠,使点 与点 重合,折痕为 .若 , ,那么线段 的长为( ) A、4 B、6 C、 D、10. 如图所示,抛物线 的图象与 轴交于 和 ,其中 .现存在以下结论;① ;② ;③ ;④ .其中正确的结论个数有( )
A、4 B、6 C、 D、10. 如图所示,抛物线 的图象与 轴交于 和 ,其中 .现存在以下结论;① ;② ;③ ;④ .其中正确的结论个数有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 计算:12. 因式分解: .13. 请写出一个开口向下,经过原点的二次函数的表达式 .14. 一个质地均匀的小正方体,六个面分别标有数字“1”、“2”、“3”、“4”、“5”、“6”,掷一次小正方体后,观察朝上一面的数字出现偶数的概率是 .15. 如图, 的度数为 .
 16. 已知点 , 在抛物线 上,则 的大小关系是 .17. 如图,正三角形 的边长为 ,将线段 绕点 逆时针旋转 至 ,形成第一个扇形;将线段 绕点 逆时针旋转 至 ,形成第二个扇形;将线段 绕点 逆时针旋转 至 ,形成第三个扇形;将线段 绕点 逆时针旋转 至 ,形成第四个扇……设 为第 个扇形的弧( ……),则 .
16. 已知点 , 在抛物线 上,则 的大小关系是 .17. 如图,正三角形 的边长为 ,将线段 绕点 逆时针旋转 至 ,形成第一个扇形;将线段 绕点 逆时针旋转 至 ,形成第二个扇形;将线段 绕点 逆时针旋转 至 ,形成第三个扇形;将线段 绕点 逆时针旋转 至 ,形成第四个扇……设 为第 个扇形的弧( ……),则 .
三、解答题
-
18. 解方程: .19. 先化简,再求值: ,其中 .20. 如图,在 中, .
 (1)、作边 的垂直平分线 ,与 , 分别相交于点 , (用尺规作图,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连接 ,若 ,求 的度数.21. 如图,等腰三角形 中, , .作 于点 ,将线段 绕着点 顺时针旋转角 后得到线段 ,连接 .
(1)、作边 的垂直平分线 ,与 , 分别相交于点 , (用尺规作图,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连接 ,若 ,求 的度数.21. 如图,等腰三角形 中, , .作 于点 ,将线段 绕着点 顺时针旋转角 后得到线段 ,连接 . (1)、求证: ;(2)、延长线段 ,交线段 于点 .求 的度数(用含有 的式子表示) .22. 如图,李师傅想用长为 米的栅栏,再借助教学楼的外墙围成一个矩形的活动区 .已知教学楼外墙长50米,设矩形 的边 米,面积为 平方米.
(1)、求证: ;(2)、延长线段 ,交线段 于点 .求 的度数(用含有 的式子表示) .22. 如图,李师傅想用长为 米的栅栏,再借助教学楼的外墙围成一个矩形的活动区 .已知教学楼外墙长50米,设矩形 的边 米,面积为 平方米. (1)、李师傅可否围出一个面积为750平方米的活动区域?如果可以,求出 的值;若不行,请说明理由;(2)、当 为多少米时,活动区的面积最大?最大面积是多少?23. “校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题;
(1)、李师傅可否围出一个面积为750平方米的活动区域?如果可以,求出 的值;若不行,请说明理由;(2)、当 为多少米时,活动区的面积最大?最大面积是多少?23. “校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题; (1)、接受问卷调查的学生共有 ▲ 人,并补全统计图;(2)、扇形统计图中“不了解”部分所对应扇形的圆心角的度数为;(3)、若该中学共有学生 人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为人;(4)、若从对校园安全知识达到“基本了解”程度的 名男生和 名女生中随机抽取 人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到 名男生和 名女生的概率.
(1)、接受问卷调查的学生共有 ▲ 人,并补全统计图;(2)、扇形统计图中“不了解”部分所对应扇形的圆心角的度数为;(3)、若该中学共有学生 人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为人;(4)、若从对校园安全知识达到“基本了解”程度的 名男生和 名女生中随机抽取 人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到 名男生和 名女生的概率.