广东省汕头市潮阳区铜盂镇2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-23 类型:期末考试
一、单选题
-
1. 的倒数是( )A、 B、 C、8 D、-82. 一元二次方程 中,二次项系数和一次项系数分别是( )A、1,4 B、1,-4 C、1,-1 D、 ,3. 下列图形中,既是轴对称又是中心对称图形的是( )A、菱形 B、等边三角形 C、平行四边形 D、等腰梯形4. 若一个正 边形的每个内角为150°,则这个正 边形的边数是( )A、10 B、11 C、12 D、135. 方程 的两根之和为( )A、-6 B、5 C、-5 D、16. 抛物线 的对称轴是 ( )A、直线x=-1 B、直线x=1 C、直线x=-2 D、直线x=27. 把抛物线y=12x2﹣1先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为( )A、y=12(x+1)2﹣3 B、y=12(x﹣1)2﹣3 C、y=12(x+1)2+1 D、y=12(x﹣1)2+18. 直角三角形两直角边长分别为 和1,那么它的外接圆的直径是( )A、1 B、2 C、3 D、49. 如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠D=40°,则∠A的度数为( )
 A、20° B、25° C、30° D、40°10. 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(3,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( )
A、20° B、25° C、30° D、40°10. 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(3,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( ) A、①② B、②③ C、①②④ D、②③④
A、①② B、②③ C、①②④ D、②③④二、填空题
-
11. 方程 的解是 .12. 已知满足 ,则 .13. 不等式组 的解集为 .14. 如图,正六边形ABCDEF内接于⊙O,若AB=2,则⊙O的半径为 .
 15. 在平面直角坐标系中,点 关于原点对称的点的坐标为 .16. 如图,已知O的半径为13,弦AB长为24,则点O到AB的距离是.
15. 在平面直角坐标系中,点 关于原点对称的点的坐标为 .16. 如图,已知O的半径为13,弦AB长为24,则点O到AB的距离是. 17. 如图所示,在平面直角坐标系中,A(4,0),B(0,2),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是 .
17. 如图所示,在平面直角坐标系中,A(4,0),B(0,2),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是 .
三、解答题
-
18. 解一元二次方程:x2﹣2x﹣3=0.19. 如图,在正方形 中,点 、 分别在 、 边上,且 ,联结 、 .求证: .
 20. 今年我国发生了较为严重的新冠肺炎疫情,口罩供不应求.某商店恰好年前新进了一批口罩,若按每个盈利1元销售,每天可售出200个,如果每个口罩的售价上涨0.5元,则销售量就减少10件,问应将每件涨价多少元时,才能让顾客得到实惠的同时每天利润为480元?21. 一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.(1)、用树状图或列表等方法列出所有可能出现的结果;(2)、求两次摸到的球的颜色不同的概率.22. 已知抛物线 经过点 和点 .
20. 今年我国发生了较为严重的新冠肺炎疫情,口罩供不应求.某商店恰好年前新进了一批口罩,若按每个盈利1元销售,每天可售出200个,如果每个口罩的售价上涨0.5元,则销售量就减少10件,问应将每件涨价多少元时,才能让顾客得到实惠的同时每天利润为480元?21. 一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.(1)、用树状图或列表等方法列出所有可能出现的结果;(2)、求两次摸到的球的颜色不同的概率.22. 已知抛物线 经过点 和点 .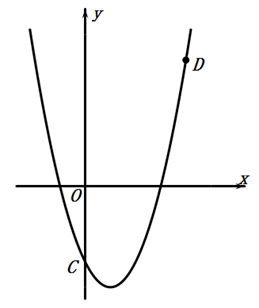 (1)、求抛物线的解析式;(2)、设抛物线与 轴的交点 、 的坐标(注:点 在点 的左边),求 的面积.23. 中, , ,将 绕点 按顺时针旋转 得到 ,连接 , ,它们交于 点.
(1)、求抛物线的解析式;(2)、设抛物线与 轴的交点 、 的坐标(注:点 在点 的左边),求 的面积.23. 中, , ,将 绕点 按顺时针旋转 得到 ,连接 , ,它们交于 点. (1)、求证: .(2)、当 ,求 的度数.24. 如图,⊙O 的半径为1,直线CD 经过圆心O,交⊙O 于C、D 两点,直径AB⊥CD,点 M 是直线CD 上异于点C、O、D 的一个动点,AM 所在的直线交⊙O 于点N,点 P 是直线CD 上另一点,且PM=PN.
(1)、求证: .(2)、当 ,求 的度数.24. 如图,⊙O 的半径为1,直线CD 经过圆心O,交⊙O 于C、D 两点,直径AB⊥CD,点 M 是直线CD 上异于点C、O、D 的一个动点,AM 所在的直线交⊙O 于点N,点 P 是直线CD 上另一点,且PM=PN. (1)、当点 M 在⊙O 内部,如图①,试判断 PN 与⊙O 的关系,并写出证明过程;(2)、当点 M 在⊙O 外部,如图②,其他条件不变时,(1)的结论是否还成立? 请说明理由;(3)、当点 M 在⊙O 外部,如图③,∠AMO=15°,求图中阴影部分的面积.25. 如图,抛物线 与 轴相交于 两点,点 在点 的右侧,与 轴相交于点 .
(1)、当点 M 在⊙O 内部,如图①,试判断 PN 与⊙O 的关系,并写出证明过程;(2)、当点 M 在⊙O 外部,如图②,其他条件不变时,(1)的结论是否还成立? 请说明理由;(3)、当点 M 在⊙O 外部,如图③,∠AMO=15°,求图中阴影部分的面积.25. 如图,抛物线 与 轴相交于 两点,点 在点 的右侧,与 轴相交于点 .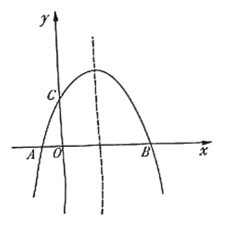 (1)、求点 的坐标;(2)、在抛物线的对称轴上有一点 ,使 的值最小,求点 的坐标;(3)、点 为 轴上一动点,在抛物线上是否存在一点 ,使以 四点构成的四边形为平行四边形?若存在,求点 的坐标;若不存在,请说明理由.
(1)、求点 的坐标;(2)、在抛物线的对称轴上有一点 ,使 的值最小,求点 的坐标;(3)、点 为 轴上一动点,在抛物线上是否存在一点 ,使以 四点构成的四边形为平行四边形?若存在,求点 的坐标;若不存在,请说明理由.