广东省梅州市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-23 类型:期末考试
一、单选题
-
1. 的绝对值是( )A、2 B、-2 C、 D、2. 如图,是一个几何体的表面展开图,则该几何体是( )
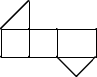 A、正方体 B、长方体 C、三棱柱 D、四棱锥3. 下列计算结果等于x3的是( )
A、正方体 B、长方体 C、三棱柱 D、四棱锥3. 下列计算结果等于x3的是( )
A、x6÷x2 B、x4﹣x C、x+x2 D、x2•x4. 一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( ) A、10° B、15° C、18° D、30°5. 布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出第二个球,两次都摸出白球的概率是( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是 ( )A、
A、10° B、15° C、18° D、30°5. 布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出第二个球,两次都摸出白球的概率是( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是 ( )A、 B、
B、 C、
C、 D、
D、 7. 如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为( )
7. 如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为( ) A、 B、2 C、 D、38. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
A、 B、2 C、 D、38. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( ) A、 B、6 C、4 D、59. 2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平,自1月底抗击“新冠病毒”以来,消毒液霱求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销.下面表示2020年初至脱销期间,该厂库存量y(吨)与时间(天)之间函数关系的大致图象是( )A、
A、 B、6 C、4 D、59. 2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平,自1月底抗击“新冠病毒”以来,消毒液霱求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销.下面表示2020年初至脱销期间,该厂库存量y(吨)与时间(天)之间函数关系的大致图象是( )A、 B、
B、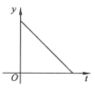 C、
C、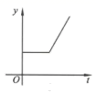 D、
D、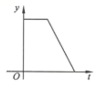 10. 如图,点B在反比例函数 ( )的图象上,点C在反比例函数 ( )的图象上,且 轴, ,垂足为点C , 交y轴于点A , 则 的面积为 ( )
10. 如图,点B在反比例函数 ( )的图象上,点C在反比例函数 ( )的图象上,且 轴, ,垂足为点C , 交y轴于点A , 则 的面积为 ( )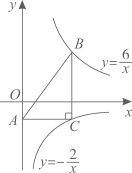 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
11. 使得代数式 有意义的 的取值范围是 .
12. 分解因式: =13. 空气的密度是 ,把 用科学记数法表示为 .14. 若a+b=3,a2+b2=7,则ab= .15. 已知关于x的一元二次方程 有一个根为 ,则a的值为 .16. 已知:如图,在 中,点 在边 上, ,则 度.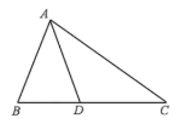 17. 点 是平行四边形 的对称中心, , 、 分别是 边上的点,且 ; 、 分别是 边上的点,且 ;若 , 分别表示 和 的面积,则 , 之间的等量关系是 .
17. 点 是平行四边形 的对称中心, , 、 分别是 边上的点,且 ; 、 分别是 边上的点,且 ;若 , 分别表示 和 的面积,则 , 之间的等量关系是 .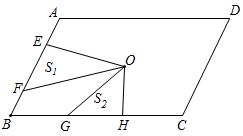
三、解答题
-
18. 计算: .19. 先化简,再求值: ,其中 , .20. 如图,已知在正方形ABCD中,M是BC边上一定点,连接AM,请用尺规作图法,在AM上求作一点P,使得△DPA∽△ABM(不写做法保留作图痕迹)
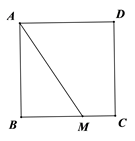 21. 已知:如图,在 中,点O是 的中点,连接 并延长,交 的延长线于点E,求证: .
21. 已知:如图,在 中,点O是 的中点,连接 并延长,交 的延长线于点E,求证: .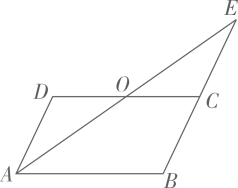 22. 2020年,新型冠状病毒肆虐全球,疫情期间学生在家进行网课学习和锻炼,学习和身体健康状况都有一定的影响.为了解学生身体健康状况,某校对学生进行立定跳远水平测试.随机抽取50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
22. 2020年,新型冠状病毒肆虐全球,疫情期间学生在家进行网课学习和锻炼,学习和身体健康状况都有一定的影响.为了解学生身体健康状况,某校对学生进行立定跳远水平测试.随机抽取50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.学生立定跳远测试成绩的频数分布表
分组
频数
a
12
b
10
学生立定跳远测试成绩的频数分布直方图
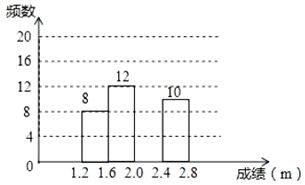
请根据图表中所提供的信息,完成下列问题:
(1)、表中 , ;(2)、样本成绩的中位数落在范围内;(3)、请把频数分布直方图补充完整;(4)、该校共有1200名学生,估计该学校学生立定跳远成绩在 范围内的有多少人?23. 甲、乙两支工程队修建二级公路,已知甲队每天修路的长度是乙队的2倍,如果两队各自修建公路500m , 甲队比乙队少用5天.(1)、求甲,乙两支工程队每天各修路多少米?(2)、我市计划修建长度为3600 m的二级公路,因工程需要,须由甲、乙两支工程队来完成.若甲队每天所需费用为1.2万元,乙队每天所需费用为0. 5万元,求在总费用不超过40万元的情况下,至少安排乙队施工多少天?24. 已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点. (1)、求证:△BGF≌△FHC;(2)、设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.25. 如图,矩形 中,点 为对角线 所在直线上的一个动点,连接 ,过点 作 ,交直线 于点 ,过点 作 ,交直线 于点 ,交直线 于点 . , .
(1)、求证:△BGF≌△FHC;(2)、设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.25. 如图,矩形 中,点 为对角线 所在直线上的一个动点,连接 ,过点 作 ,交直线 于点 ,过点 作 ,交直线 于点 ,交直线 于点 . , .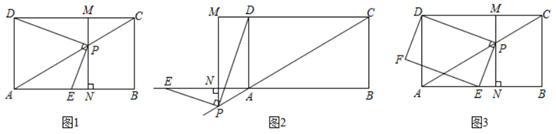 (1)、如图 ,①当点 在线段 上时, 和 的数量关系为: ;
(1)、如图 ,①当点 在线段 上时, 和 的数量关系为: ;② 的值是;
(2)、如图 ,当点 在 延长线上时,(1)中的结论②是否成立?若成立,请证明;若不成立,说明理由;(3)、如图 ,以线段 , 为邻边作矩形 .设 的长为 ,矩形 的面积为 .请直接写出 与 之间的函数关系式及 的最小值.