广东省揭阳市普宁市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-23 类型:期末考试
一、单选题
-
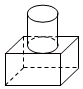
1. 如图,一个由圆柱和长方体组成的几何体水平放置,它的俯视图是( )
 A、
A、 B、
B、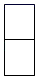 C、
C、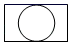 D、
D、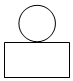 2. 用公式法解方程3x2+5x+1=0,正确的是( )A、 B、 C、 D、3. 已知关于x的一元二次方程x2+bx﹣1=0,则下列关于该方程根的判断,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关4. 在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.若随机摸出一个小球后不放回,再随机摸出一个小球,则两次取出小球标号的和等于5的概率为( )A、 B、 C、 D、5. 如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
2. 用公式法解方程3x2+5x+1=0,正确的是( )A、 B、 C、 D、3. 已知关于x的一元二次方程x2+bx﹣1=0,则下列关于该方程根的判断,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关4. 在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.若随机摸出一个小球后不放回,再随机摸出一个小球,则两次取出小球标号的和等于5的概率为( )A、 B、 C、 D、5. 如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )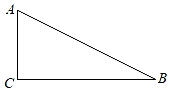 A、sinA= B、a=sinB×c C、cosA= D、tanA=6. 用配方法将二次函数y=x2﹣8x﹣9化为y=a(x﹣h)2+k的形式为( )A、y=(x﹣4)2+7 B、y=(x+4)2+7 C、y=(x﹣4)2﹣25 D、y=(x+4)2﹣257. 下列说法正确的是( )A、一组对边平行另一组对边相等的四边形是平行四边形 B、对角线互相垂直平分的四边形是菱形 C、对角线相等的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形8.
A、sinA= B、a=sinB×c C、cosA= D、tanA=6. 用配方法将二次函数y=x2﹣8x﹣9化为y=a(x﹣h)2+k的形式为( )A、y=(x﹣4)2+7 B、y=(x+4)2+7 C、y=(x﹣4)2﹣25 D、y=(x+4)2﹣257. 下列说法正确的是( )A、一组对边平行另一组对边相等的四边形是平行四边形 B、对角线互相垂直平分的四边形是菱形 C、对角线相等的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形8.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
 A、
A、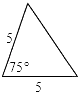 B、
B、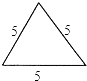 C、
C、 D、
D、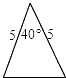 9. 如图,菱形ABCD的对角线AC、BD相交于点O , 过点D作DH⊥AB于点H , 连接OH , 若OA=6,S菱形ABCD=48,则OH的长为( )
9. 如图,菱形ABCD的对角线AC、BD相交于点O , 过点D作DH⊥AB于点H , 连接OH , 若OA=6,S菱形ABCD=48,则OH的长为( )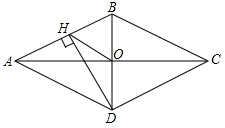 A、4 B、8 C、 D、610. 若函数 的图象如图所示,则函数 和 在同一平面直角坐标系中的图象大致是( )
A、4 B、8 C、 D、610. 若函数 的图象如图所示,则函数 和 在同一平面直角坐标系中的图象大致是( )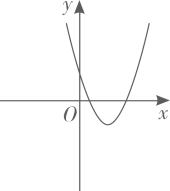 A、
A、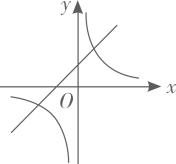 B、
B、 C、
C、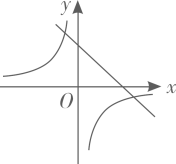 D、
D、
二、填空题
-
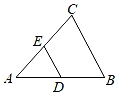
11. 计算:tan260°+4sin30°﹣2cos45°= .12. 设 , 是方程 的两个实数根,则 的值为 .13. 如图,在△ABC中,D是AB中点,DE∥BC,若DE=6,则BC= .
 14. 如图,在平面直角坐标系中, 是坐标原点,在 中, 于点 ,点 在反比例函数 的图象上,若OB=4,AC=3,则 的值为 .
14. 如图,在平面直角坐标系中, 是坐标原点,在 中, 于点 ,点 在反比例函数 的图象上,若OB=4,AC=3,则 的值为 . 15. 抛物线 与x轴有交点,则k的取值范围是.16. 如图所示,在四边形 中, , , .连接 , ,若 ,则 长度是 .
15. 抛物线 与x轴有交点,则k的取值范围是.16. 如图所示,在四边形 中, , , .连接 , ,若 ,则 长度是 .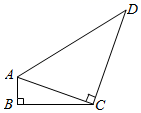 17. 如图, 为平行四边形 边 上一点, 分别为 上的点,且 的面积分别记为 .若 则 .
17. 如图, 为平行四边形 边 上一点, 分别为 上的点,且 的面积分别记为 .若 则 .
三、解答题
-
18. 用配方法解方程:19. 随着“新冠肺炎”疫情防控形势日渐好转,各地开始复工复学,某校复学后成立“防疫志愿者服务队”,设立四个“服务监督岗”:①洗手监督岗,②戴口罩监督岗,③就餐监督岗,④操场活动监督岗.李老师和王老师报名参加了志愿者服务工作,学校将报名的志愿者随机分配到四个监督岗.用列表法或画树状图法,求李老师和王老师被分配到同一个监督岗的概率.20. 已知二次函数 (b,c为常数)的图象经过点(0,3),(﹣1,0).
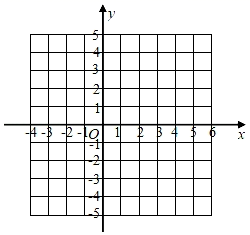 (1)、则b= , c=;(2)、该二次函数图象的顶点坐标为;(3)、在所给坐标系中画出该二次函数的图象;(4)、根据图象,当﹣1<x<0时,y的取值范围是 .21. B,D两地间有一段笔直的高速铁路,长度为100km,某时发生的地震对地面上以点A为圆心,30km为半径的圆形区域内的建筑物有影响,分别从B,D两地处测得点A的方位角如图所示,高速铁路是否会受到地震的影响?请通过计算说明理由.(结果精确到0.1km,参考数据: )
(1)、则b= , c=;(2)、该二次函数图象的顶点坐标为;(3)、在所给坐标系中画出该二次函数的图象;(4)、根据图象,当﹣1<x<0时,y的取值范围是 .21. B,D两地间有一段笔直的高速铁路,长度为100km,某时发生的地震对地面上以点A为圆心,30km为半径的圆形区域内的建筑物有影响,分别从B,D两地处测得点A的方位角如图所示,高速铁路是否会受到地震的影响?请通过计算说明理由.(结果精确到0.1km,参考数据: )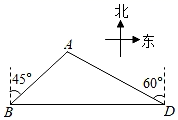 22. 某商店销售一种成本为40元的玩具,若按每件50元销售,一个月可售出500件,销售价每涨1元,月销量就减少10件(1)、商店要使月销售利润达到8000元,销售价应定为每件多少元?(2)、当销售价定为每件多少元时会获得最大利润?23. 如图,正方形ABCD中,点E , F分别在边,AD , CD上,且 ,BD和EF交于点O , 延长BD至点H , 使得 ,并连接HE , HF .
22. 某商店销售一种成本为40元的玩具,若按每件50元销售,一个月可售出500件,销售价每涨1元,月销量就减少10件(1)、商店要使月销售利润达到8000元,销售价应定为每件多少元?(2)、当销售价定为每件多少元时会获得最大利润?23. 如图,正方形ABCD中,点E , F分别在边,AD , CD上,且 ,BD和EF交于点O , 延长BD至点H , 使得 ,并连接HE , HF .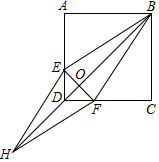 (1)、求证: ;(2)、试判断四边形BEHF是什么特殊的四边形,并说明理由.24. 如图在平面直角坐标系中,一次函数 的图像经过点 、 交反比例函数 的图像于点 ,点 在反比例函数的图象上,横坐标为 , 轴交直线 于点 , 是 轴上任意一点,连接 、 .
(1)、求证: ;(2)、试判断四边形BEHF是什么特殊的四边形,并说明理由.24. 如图在平面直角坐标系中,一次函数 的图像经过点 、 交反比例函数 的图像于点 ,点 在反比例函数的图象上,横坐标为 , 轴交直线 于点 , 是 轴上任意一点,连接 、 . (1)、求一次函数和反比例函数的表达式;(2)、求 面积的最大值.25. 如图,在四边形ABCD和Rt△EBF中,AB∥CD,CD>AB,点C在EB上,∠ABC=∠EBF=90°,AB=BE=8cm,BC=BF=6cm,延长DC交EF于点M,点P从点A出发,沿AC方向匀速运动,速度为2cm/s;同时,点Q从点M出发,沿MF方向匀速运动,速度为1cm/s,过点P作GH⊥AB于点H,交CD于点G,设运动时间为t(s)(0<t≤5);
(1)、求一次函数和反比例函数的表达式;(2)、求 面积的最大值.25. 如图,在四边形ABCD和Rt△EBF中,AB∥CD,CD>AB,点C在EB上,∠ABC=∠EBF=90°,AB=BE=8cm,BC=BF=6cm,延长DC交EF于点M,点P从点A出发,沿AC方向匀速运动,速度为2cm/s;同时,点Q从点M出发,沿MF方向匀速运动,速度为1cm/s,过点P作GH⊥AB于点H,交CD于点G,设运动时间为t(s)(0<t≤5);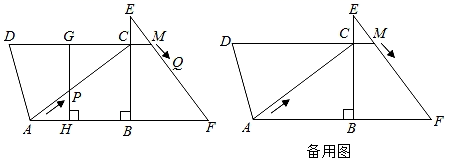 (1)、当t为何值时,CM=QM?(2)、连接PQ,作QN⊥AF于点N,当四边形PQNH为矩形时,求t的值;(3)、连接QC,QH,设四边形QCGH的面积为S(cm2),求S与t的函数关系式.
(1)、当t为何值时,CM=QM?(2)、连接PQ,作QN⊥AF于点N,当四边形PQNH为矩形时,求t的值;(3)、连接QC,QH,设四边形QCGH的面积为S(cm2),求S与t的函数关系式.