广东省揭阳市惠来县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-23 类型:期末考试
一、单选题
-
1. 在-0.5、-1、0、5这四个有理数中,最小的有理数是( )A、-1 B、-0.5 C、0 D、52. 在下列所给出坐标的点中,在第四象限的是( )A、 B、 C、 D、3. 如图所示的几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、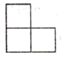 4. 反比例函数y=﹣ 的图象在( )A、第一、三象限 B、第一、二象限 C、第二、四象限 D、第三、四象限5. 若一个多边形每一个内角都为144°,则这个多边形是( )边形A、6 B、8 C、10 D、126. 用配方法解方程 ,下列配方正确的是( )A、 B、 C、 D、7. 如图,有6张扑克牌,从中随机抽取一张,点数为偶数的概率是( )
4. 反比例函数y=﹣ 的图象在( )A、第一、三象限 B、第一、二象限 C、第二、四象限 D、第三、四象限5. 若一个多边形每一个内角都为144°,则这个多边形是( )边形A、6 B、8 C、10 D、126. 用配方法解方程 ,下列配方正确的是( )A、 B、 C、 D、7. 如图,有6张扑克牌,从中随机抽取一张,点数为偶数的概率是( ) A、 B、 C、 D、8. 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
A、 B、 C、 D、8. 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )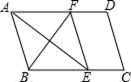 A、10 B、12 C、16 D、189. 如图,在 中, , .按下列步骤作图:①分别以点B和点C为圆心,大于 一半的长为半径作圆弧,两弧相交于点M和点N;②作直线 ,与边 相交于点D,连结 .下列说法不一定正确的是( )
A、10 B、12 C、16 D、189. 如图,在 中, , .按下列步骤作图:①分别以点B和点C为圆心,大于 一半的长为半径作圆弧,两弧相交于点M和点N;②作直线 ,与边 相交于点D,连结 .下列说法不一定正确的是( )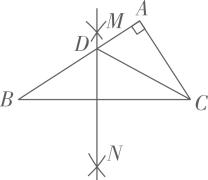 A、 B、 C、 D、10. 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E.F分别在BC和CD上,下列结论:
A、 B、 C、 D、10. 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E.F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④正方形对角线AC=1+ , 其中正确的序号是( )
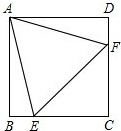 A、①②④ B、①② C、②③④ D、①③④
A、①②④ B、①② C、②③④ D、①③④二、填空题
-
11. 港珠澳大桥被英国《卫报》誉为“新世界七大奇迹”之一,它是世界总体跨度最长的跨海大桥,全长55000米.数字55000用科学记数法表示为.12. 把ab2﹣ab分解因式的结果是.13. 小明希望测量出电线杆AB的高度,于是在阳光明媚的一天,他在电线杆旁的点D处立一标杆CD,使标杆的影子DE与电线杆的影子BE部分重叠(即点E、C、A在一直线上),量得ED=2米,DB=4米,CD=1.5米,则电线杆AB长为
 14. 若 +|b﹣2|=0,则(a+b)2020的值为 .15. 已知: , ,则 的值为 .16. 如图,P1是反比例函数 (k>0)在第一象限图象上的一点,点A1的坐标为(2,0).若△P1OA1与△P2A1A2均为等边三角形,则A2点的坐标为 .
14. 若 +|b﹣2|=0,则(a+b)2020的值为 .15. 已知: , ,则 的值为 .16. 如图,P1是反比例函数 (k>0)在第一象限图象上的一点,点A1的坐标为(2,0).若△P1OA1与△P2A1A2均为等边三角形,则A2点的坐标为 . 17. 如图,在平行四边形ABCD中,AB=2,BC=5.∠BCD的平分线交AD于点F , 交BA的延长线于点E , 则AE的长为 .
17. 如图,在平行四边形ABCD中,AB=2,BC=5.∠BCD的平分线交AD于点F , 交BA的延长线于点E , 则AE的长为 .
三、解答题
-
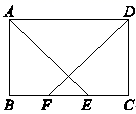
18. 计算: ﹣| ﹣2|+( )﹣2 .19. 解方程: .20. 如图,在矩形 中, .求证: .
 21. 如图,正方形FGHI各顶点分别在△ABC各边上,AD是△ABC的高, BC=10,AD=6.
21. 如图,正方形FGHI各顶点分别在△ABC各边上,AD是△ABC的高, BC=10,AD=6.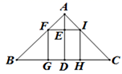 (1)、证明:△AFI∽△ABC;(2)、求正方形FGHI的边长.22. 一个不透明的口袋中有三个完全相同的小球,球上分别标有数字-1,1,2,第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y。(1)、用列表法或画树状图法,列出点M(x,y)的所有可能结果。(2)、求点M(x,y)在反比例函数y= 的图象上的概率。23. 为做好延迟开学期间学生的在线学习服务工作,市教育局推出“中小学延迟开学期间网络课堂”,为学生提供线上学习,据统计,第一批公益课受益学生20万人次,第三批公益课受益学生24.2万人次.(1)、如果第二批,第三批公益课受益学生人次的增长率相同,求这个增长率;(2)、按照这个增长率,预计第四批公益课受益学生将达到多少万人次?24. 如图,在平面直角坐标系xOy中,直线y=2x+2与函数y= (k≠0)的图象交于A , B两点,且点A的坐标为(1,m).
(1)、证明:△AFI∽△ABC;(2)、求正方形FGHI的边长.22. 一个不透明的口袋中有三个完全相同的小球,球上分别标有数字-1,1,2,第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y。(1)、用列表法或画树状图法,列出点M(x,y)的所有可能结果。(2)、求点M(x,y)在反比例函数y= 的图象上的概率。23. 为做好延迟开学期间学生的在线学习服务工作,市教育局推出“中小学延迟开学期间网络课堂”,为学生提供线上学习,据统计,第一批公益课受益学生20万人次,第三批公益课受益学生24.2万人次.(1)、如果第二批,第三批公益课受益学生人次的增长率相同,求这个增长率;(2)、按照这个增长率,预计第四批公益课受益学生将达到多少万人次?24. 如图,在平面直角坐标系xOy中,直线y=2x+2与函数y= (k≠0)的图象交于A , B两点,且点A的坐标为(1,m). (1)、求k , m的值;(2)、直接写出关于x的不等式2x+2> 的解集;(3)、若Q在x轴上,△ABQ的面积是6,求Q点坐标.25. 已知,矩形ABCD中,AB=4cm , BC=8cm , AC的垂直平分线EF分别交AD、BC于点E、F , 垂足为O .
(1)、求k , m的值;(2)、直接写出关于x的不等式2x+2> 的解集;(3)、若Q在x轴上,△ABQ的面积是6,求Q点坐标.25. 已知,矩形ABCD中,AB=4cm , BC=8cm , AC的垂直平分线EF分别交AD、BC于点E、F , 垂足为O . (1)、如图(1),连接AF、CE .
(1)、如图(1),连接AF、CE .①四边形AFCE是什么特殊四边形?说明理由;
②求AF的长;
(2)、如图(2),动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,已知点P的速度为每秒5cm , 点Q的速度为每秒4cm , 运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.