广东省江门市2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 小明做抛币实验，连续抛了5次都是反面向上，当他抛第6次时，反面向上是一件（）事件

A、必然 B、不可能 C、确定 D、随机

查看试题解析
2. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 点 $A$ 的坐标为 $(2 ， 3)$ ，则点 $A$ 关于 $y$ 轴的对称点 $A^{'}$ 的坐标为（）．

A、 $(- 2 ， 3)$ B、 $(2 ， - 3)$ C、 $(3 ， 2)$ D、 $(- 2 ， - 3)$

查看试题解析
4. 已知x=2是关于x的一元二次方程x²﹣x﹣2a=0的一个解，则a的值为（）

A、0 B、﹣1 C、1 D、2

查看试题解析
5. 抛物线y=(x+1)²＋2的对称轴是（　　）

A、直线x=－1 B、直线x=1 C、直线y=－1 D、直线y=1

查看试题解析
6. 若A（-4， $y_{1}$ ），B（-1， $y_{2}$ ），C（2， $y_{3}$ ）为二次函数y＝- $x^{2}$ ＋4x＋5图象上的三点，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（）

A、 $y_{3}$ < $y_{1}$ < $y_{2}$ B、 $y_{3}$ < $y_{2}$ < $y_{1}$ C、 $y_{1}$ < $y_{2}$ < $y_{3}$ D、 $y_{2}$ < $y_{1}$ < $y_{3}$

查看试题解析
7. 如图，△ABC内接于⊙O，若∠A＝α度，则∠OBC的度数为（）

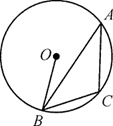A、α B、90－α C、90＋α D、90＋2α

查看试题解析
8. 当ab>0时，y=ax²与y=ax+b的图象大致是（）

A、 B、 C、 D、

查看试题解析
9. 如图，抛物线y=ax²+bx+c（a＞0）的对称轴是直线x=1，且经过点P（3，0），则a-b+c的值为（）

A、0 B、-1 C、1 D、2

查看试题解析
10. 一条公路弯道处是一段圆弧弧AB，点O是这条弧所在圆的圆心，点C是弧AB的中点，OC与AB相交于点D．已知AB=120m，CD=20m，那么这段弯道的半径为（）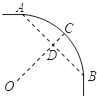

A、200m B、200 $\sqrt{3}$ m C、100m D、100 $\sqrt{3}$ m

查看试题解析

二、填空题

11. 方程x²＝2x的解是.

查看试题解析
12. 若点 $A (a - 2 ， b + 2)$ 与点 $B (4 ， - 3)$ 关于原点对称，则 $a - b =$ ．

查看试题解析
13. 如图，函数 $y = x$ 与 $y = \frac{16}{x}$ 的图象交于 $A$ 、 $B$ 两点，过点 $A$ 作 $A C$ 垂直于 $y$ 轴，垂足为 $C$ ，则 $△ A B C$ 的面积为．

查看试题解析
14. 如图，半圆O的直径AB=2，弦CD∥AB，∠COD=90°，则图中阴影部分的面积为．

查看试题解析
15. 将抛物线 $y = 2 {(x - 4)}^{2} - 1$ 向平移个单位，向平移个单位可得抛物线 $y = 2 x^{2}$ ．

查看试题解析
16. 若函数 $y = （ a + 1 ） x^{2} - 4 x + 2 a$ 的图像与x轴有且只有一个交点，则a的值为 .

查看试题解析
17. 已知二次函数y＝x²﹣2x+2在t≤x≤t+1时的最小值是t，则t的值为.

查看试题解析

三、解答题

18. 解方程： $x^{2} + 5 x + 8 = 2 (x + 4)$ ．

查看试题解析
19. 已知反比例函数 $y = - \frac{k}{x}$ 和一次函数 $y = k x + 2 (k \neq 0)$ 的图象只有一个公共点，求 $k$ 的值．

查看试题解析
20. △ABC在平面直角坐标系中的位置如图所示．

(1)、作出△ABC关于原点对称的图形△A₁B₁C₁；

(2)、写出点A₁、B₁、C₁坐标。

查看试题解析
21. 如图，有一座圆弧形拱桥，桥下水面宽度AB为12m，拱高CD为4m.

(1)、求拱桥的半径；

(2)、有一艘宽为5m的货船，船舱顶部为长方形，并高出水面3.4m，则此货船是否能顺利通过此圆弧形拱桥，并说明理由；

查看试题解析

22. 在大课间活动中，体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试，并对成绩进行统计分析，绘制了频数分布表和统计图，请你根据图表中的信息完成下列问题：

分组	频数	频率
第一组（0≤x＜15）	3	0.15
第二组（15≤x＜30）	6	a
第三组（30≤x＜45）	7	0.35
第四组（45≤x＜60）	b	0.20

(1)、频数分布表中a= ， b= ，并将统计图补充完整；

(2)、如果该校七年级共有女生180人，估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人？

(3)、已知第一组中只有一个甲班学生，第四组中只有一个乙班学生，老师随机从这两个组中各选一名学生谈心得体会，则所选两人正好都是甲班学生的概率是多少？

查看试题解析

23. “丹棱冻粑”是眉山著名特色小吃，产品畅销省内外，现有一个产品销售点在经销时发现：如果每箱产品盈利10元，每天可售出50箱；若每箱产品涨价1元，日销售量将减少2箱．

(1)、现该销售点每天盈利600元，同时又要顾客得到实惠，那么每箱产品应涨价多少元？

(2)、若该销售点单纯从经济角度考虑，每箱产品应涨价多少元才能获利最高？

查看试题解析
24. 如图，⊙O的直径 $AB = 4$ ， $∠ ABC = 30 °$ ， $BC = 4 \sqrt{3}$ ， $D$ 是线段 $B C$ 的中点．

(1)、试判断点 $D$ 与⊙O的位置关系，并说明理由；

(2)、过点 $D$ 作 $DE ⊥ AC$ ，垂足为点 $E$ ，求证：直线 $D E$ 是⊙O的切线．

查看试题解析
25. 在平面直角坐标系中，已知抛物线 $y = a x^{2} + b x - 4$ 与 $x$ 轴相交于 $A (- 4 ， 0)$ 、 $C (2 ， 0)$ 两点．与 $y$ 轴相交于点 $B$ ．

(1)、求抛物线的解析式；

(2)、求抛物线与 $y$ 轴的交点 $B$ 的坐标和抛物线顶点坐标；

(3)、若点 $M$ 为第三象限内抛物线上一动点，点 $M$ 的横坐标为 $m$ ， $△ A M B$ 的面积为 $S$ ．求 $S$ 关于 $m$ 的函数关系式，并求出 $S$ 的最大值．

查看试题解析