广东省广州市越秀区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

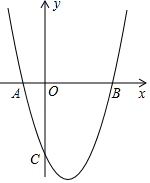
1. 如果2是方程 $x^{2} - x + c = 0$ 的一个根，则常数c的值是（）

A、1 B、2 C、－1 D、－2

查看试题解析
2. 窗棂即窗格（窗里面的横的或竖的格）是中国传统木构建筑的框架结构设计．下列表示我国古代窗棂样式结构图案中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图是由五个相同的小立方块搭成的几何体，这个几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列事件中，是随机事件的是（）

A、任意画两个直角三角形，这两个三角形相似 B、相似三角形的对应角相等 C、⊙O的半径为5，OP＝3，点P在⊙O外 D、直径所对的圆周角为直角

查看试题解析
5. 在 $Rt$ △ $A B C$ 中，∠ $C = 90 °$ ，如果 $A C = 4$ ， $B C = 3$ ，那么cosA的值为（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析
6. 如图⊙P经过点A（0， $\sqrt{3}$ ）、O（0，0）、B（1，0），点C在第一象限的 $\overset{⌢}{A B}$ 上，则∠BCO的度数为（）

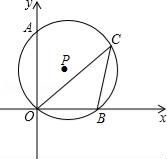A、15° B、30° C、45° D、60°

查看试题解析
7. 已知正比例函数 $y_{1}$ 的图象与反比例函数 $y_{2}$ 图象相交于点 $A (2, 4)$ ，下列说法正确的是（）

A、反比例函数 $y_{2}$ 的解析式是 $y_{2} = - \frac{8}{x}$ B、两个函数图象的另一交点坐标为 $(2, - 4)$ C、当 $x < - 2$ 或 $0 < x < 2$ 时， $y_{1} < y_{2}$ D、正比例函数 $y_{1}$ 与反比例函数 $y_{2}$ 都随 $x$ 的增大而增大

查看试题解析
8. 南洞庭大桥是南益高速公路上的重要桥梁，小芳同学在校外实践活动中对此开展测量活动．如图，在桥外一点A测得大桥主架与水面的交汇点C的俯角为α，大桥主架的顶端D的仰角为β，已知测量点与大桥主架的水平距离AB＝a，则此时大桥主架顶端离水面的高CD为（）

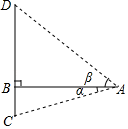A、asinα+asinβ B、acosα+acosβ C、atanα+atanβ D、 $\frac{a}{\tan α} + \frac{a}{\tan β}$

查看试题解析
9. 已知反比例函数 y＝ $\frac{a b}{x}$ 的图象如图所示，则二次函数 y =ax ²－2x和一次函数 y＝bx+a 在同一平面直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，正方形ABCD中，AB＝6，E为AB的中点，将△ADE沿DE翻折得到△FDE，延长EF交BC于G，FH⊥BC，垂足为H，连接BF、DG.以下结论：①BF∥ED；②△DFG≌△DCG；③△FHB∽△EAD；④tan∠GEB＝ $\frac{4}{3}$ ；⑤S_△_BFG＝2.6；其中正确的个数是（）

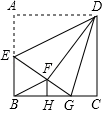A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 如图， $△ A B C$ 顺时针旋转能与 $△ A D E$ 重合，且 $∠ B A E = 70 °$ ，则旋转角是度.

查看试题解析
12. 在英语句子“Wish you success”（祝你成功）中任选一个字母，这个字母为“s”的概率是.

查看试题解析
13. 关于x的方程x²+3x+k﹣1＝0有两个相等的实数根，则k的值为.

查看试题解析
14. 若A(－4，y₁)，B(－3，y₂)，C(1，y₃)为二次函数y＝x²＋4x－m的图象上的三点，则y₁ ， y₂ ， y₃的大小关系是

查看试题解析
15. 如图，正五边形ABCDE内接于⊙O ，连接BD ，则∠ABD＝°．

查看试题解析
16. 已知：△ABC在坐标平面内三顶点的坐标分别为A（0，2）、B（3，3）、C（2，1）．以O为位似中心画△A₁B₁C₁ ，使得△A₁B₁C₁与△ABC位似，且相似比是3，则点C的对应顶点C₁的坐标是．

查看试题解析
17. 已知一个圆锥体的三视图如图所示，将这个圆锥的侧面展开为扇形，则这个扇形的圆心角是．

查看试题解析
18. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $\sin B = \frac{4}{5}$ ，延长 $B C$ 至点 $D$ ，使 $C D ： A C = 1 ： 2$ ，则 $\tan ∠ C A D =$ .

查看试题解析
19. 如图，△OAB的顶点A在双曲线y= $\frac{6}{x}$ （x＞0）上，顶点B在双曲线y=- $\frac{4}{x}$ （x＜0）上，AB中点P恰好落在y轴上，则△OAB的面积为.

查看试题解析
20. 如图，已知⊙O的半径为1，AB ， AC是⊙O的两条弦，且AB＝AC ，延长BO交AC于点D ，连接OA ， OC ，若AD²＝AB•DC ，则OD＝．

查看试题解析

三、解答题

21. 如图，在 $R t Δ O A B$ 中， $∠ O A B = 90$ ，且点 $B$ 的坐标为 $(4 ， 3)$

(1)、画出 $Δ O A B$ 绕点 $O$ 逆时针旋转 $90 °$ 后的 $Δ O A_{1} B_{1}$ .

(2)、求点 $B$ 旋转到点 $B_{1}$ 所经过的路线长（结果保留 $π$ ）

(3)、画出 $Δ O A B$ 关于原点对称的 $Δ O A_{2} B_{2}$

查看试题解析
22. 如图，在一块长8 $m$ 、宽6 $m$ 的矩形绿地内，开辟出一个矩形的花圃，使四周的绿地等宽，已知绿地的面积与花圃的面积相等，求花圃四周绿地的宽.

查看试题解析
23. 为庆祝中华人民共和国建国70周年，某校从A、B两位男生和D、E两位女生中选派学生，参加全区中小学“我和我的祖国”演讲比赛．

(1)、如果选派一位学生参赛，那么选派到的代表是A同学的概率是；

(2)、如果选派两位学生参赛，用树状图或列表法，求恰好选派一男一女两位同学参赛的概率．

查看试题解析
24. 如图，一次函数 $y_{1} = \frac{1}{2} x + 2$ 和反比例函数 $y_{2} = \frac{k}{x} (k \neq 0)$ 的图象相交于 $A ， B$ 两点，点A的横坐标为2．

(1)、求k的值及A，B两点的坐标

(2)、当 $y_{1} > y_{2}$ 时，求x的取值范围．

查看试题解析
25. 如图，AC为圆O的直径，弦AD的延长线与过点C的切线交于点B，E为BC中点，AC= $4 \sqrt{3}$ ，BC=4.

(1)、求证：DE为圆O的切线；

(2)、求阴影部分面积.

查看试题解析
26. 如图，已知二次函数y＝x²﹣2x+m的图象与x轴交于点A、B ，与y轴交于点C ，直线AC交二次函数图象的对称轴于点D ，若点C为AD的中点．

(1)、求m的值；

(2)、若二次函数图象上有一点Q ，使得tan∠ABQ＝3，求点Q的坐标；

(3)、对于（2）中的Q点，在二次函数图象上是否存在点P ，使得△QBP∽△COA？若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析