广东省广州市白云区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 方程x²﹣1＝0的解是（）

A、x₁＝x₂＝1 B、x₁＝x₂＝﹣1 C、x＝±1 D、无实数根

查看试题解析
2. 下面的图形中，既是轴对称图形又是中心对称图形的是（）

A、 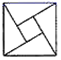B、 C、 D、

查看试题解析
3. 在下列各点中，抛物线y＝3x²经过点（）

A、（0，﹣1） B、（0，0） C、（0，1） D、（0，2）

查看试题解析
4. 如图，点 $A$ ， $B$ ， $C$ 都在 $⊙ O$ 上，若 $∠ C = 34 °$ ，则 $∠ A O B$ 为（）

A、34° B、56° C、60° D、68°

查看试题解析
5. 如图，把△OAB绕点O逆时针旋转80°，得到△OCD ，则下列结论错误的是（）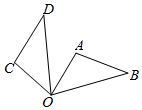

A、BD＝ $\sqrt{2}$ OB B、AB＝CD C、∠AOC＝∠BOD D、∠A＝∠C

查看试题解析
6. 若关于x的一元二次方程（m+1）x²-2x+1=0有实数根，则实数m的取值范围是（）

A、m≥0 B、m≤0 C、m≠1 D、m≤0且m≠-1

查看试题解析
7. 反比例函数y＝ $\frac{k}{x}$ 的图象经过点（﹣3，1），则下列说法错误的是（）

A、k＝﹣3 B、函数的图象在第二、四象限 C、函数图象经过点（3，﹣1） D、当x＞0时，y随x的增大而减小

查看试题解析
8. 如图，已知Rt△ABC中，∠C＝90°，∠A＝30°，AC＝6，以点B为圆心，3为半径作⊙B ，则点C与⊙B的位置关系是（）

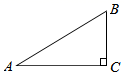A、点C在⊙B内 B、点C在⊙B上 C、点C在⊙B外 D、无法确定

查看试题解析
9. 如图，电路图上有 $4$ 个开关 $A$ 、 $B$ 、 $C$ 、 $D$ 和 $1$ 个小灯泡，同时闭合开关 $A$ 、 $B$ 或同时闭合开关 $C$ 、 $D$ 都可以使小灯泡发光.下列操作中，“小灯泡发光”这个事件是随机事件的是（）

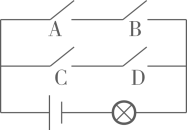A、只闭合1个开关 B、只闭合2个开关 C、只闭合3个开关 D、闭合4个开关

查看试题解析
10. 如图，抛物线y＝ax²+bx+c的对称轴为x＝﹣1，且经过点（﹣3，0）．下列结论：
①abc＜0；②若（﹣4，y₁）和（3，y₂）是抛物线上两点，则y₁＞y₂；③a+b+c＜0；④对于任意实数m ，均有am²+bm+c≥﹣4a ．

其中正确的结论的个数是（）

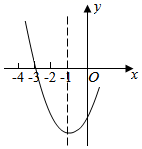A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

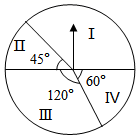
11. 点A（﹣2，3）关于原点对称的点的坐标是．

查看试题解析
12. 抛物线y＝x²﹣3x+2与x轴的交点个数是个．

查看试题解析
13. 已知一个正六边形的外接圆半径为2，则这个正六边形的周长为．

查看试题解析
14. 如图是一个可以自由转动的转盘，转盘分成四个扇形，标号分别为Ⅰ，Ⅱ，Ⅲ，Ⅳ四个数字．指针的位置固定，转动的转盘停止后，其中的某个扇形会恰好停在指针所指的位置（指针指向两个扇形的交线时，当作指向右边的扇形区域）．指针指向扇形Ⅰ的概率是．

查看试题解析
15. 如图，从一块边长为2的等边三角形卡纸上剪下一个面积最大的扇形，并将其围成一个圆锥，则圆锥的底面圆的半径是．

查看试题解析
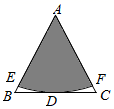16. 为了迎接2021年春节，李师傅计划改造一个长为6m，宽为4m的矩形花池ABCD ，如图，他将画线工具固定在一根4m木棍EF的中点P处．画线时，使点E ， F都在花池边的轨道上按逆时针方向滑动一周．若将点P所画出的封闭图形围成的区域全部种植年花，则种植年花的区域的面积是m² ．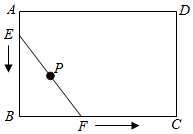

查看试题解析

三、解答题

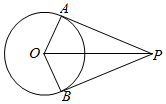
17. 解方程：x²﹣2x﹣5＝0.

查看试题解析
18. 如图，PA ， PB是⊙O的切线，A ， B为切点，连接OP ．
求证：OP平分∠AOB ．

查看试题解析
19. 在一个不透明的盒子中装有四个球，它们分别印有“我”、“爱”、“白”、“云”字样．这些球的形状、大小、质地等完全相同，即除字样外无其他差别．

(1)、随机摸出一个球，恰好摸到“爱”字球的概率为；

(2)、随机摸出一个球后，放回并摇匀，再随机摸出一个．求两次摸到的球中，至少有一次摸到“云”字球的概率．

查看试题解析
20. 如图，在平面直角坐标系xOy中，△ABC各顶点的坐标分别为A（1，1），B（5，2），C（5，5）．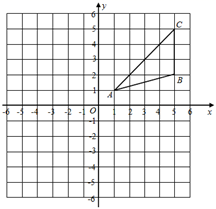

(1)、将△ABC绕点O旋转180°后，得到△A₁B₁C₁ ，画出△A₁B₁C₁；

(2)、在（1）的条件下，求旋转过程中，点B经过的路径长（结果保留π）．

查看试题解析
21. 在二次函数y＝ax²+bx+3（a ， b是常数）中，列表表示几组自变量x与函数值y的对应值：

x

…

﹣2

﹣1

0

1

2

…

y＝ax²+bx+c

…

m

0

3

n

3

…

(1)、根据以上信息，可得该二次函数的图象开口向，对称轴为；

(2)、求|m﹣n|的值．

查看试题解析
22. 如图是一张长24cm，宽12cm的矩形铁皮，将其剪去一个小正方形和两个矩形，剩余部分（阴影部分）恰好可制成一个有盖的长方体铁盒．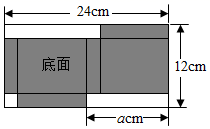

(1)、a＝；

(2)、若铁盒底面积是80cm² ，求剪去的小正方形边长．

查看试题解析
23. 如图，平面直角坐标系xOy中，点A的坐标为（2，6），直线AB∥y轴，且与x轴交于点B ，反比例函数 $y = \frac{k}{x}$ （x＞0）的图象经过点A和点P ．若⊙P经过点A ，且与x轴交于B ， C两点．

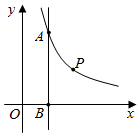(1)、求k的值和点C的坐标；

(2)、判断⊙P与y轴的位置关系，并说明理由．

查看试题解析
24. 如图

(1)、作图：如图，已知△ABC ， ∠ACB＜120°，
①作等边△ACD ，使得点D ， B分别是直线AC异侧的两个点；

②作等边△BCE ，使得点E ， A分别是直线BC异侧的两个点；

（要求尺规作图，保留作图痕迹，不写作法．）

(2)、推理：在（1）所作的图中，设直线BD ， AE的交点为P ，连接PC ，
①求∠APD的度数；

②猜想PA ， PB ， PC与AE之间的等量关系，并证明：

(3)、变式：已知△ABC ， ∠ACB＞120°，按（1）的方法作图后，设直线BD ， AE的交点为P ，连接PC ．测得∠PAB＝15°，PA＝ $\sqrt{6} + \sqrt{2}$ ，PB＝ $\sqrt{2}$ ，PC＝ $\frac{\sqrt{2}}{2}$ ．求点D到直线AB的距离．

查看试题解析
25. 已知抛物线y＝ax²+2ax﹣3a（a是常数）与x轴交于A ， B两点（点A在点B的左边），与y轴交于点C ．顶点D不在第二象限，记△ABC的面积为S₁ ， △ACD的面积为S₂ ．

(1)、当S₁＝3时，求抛物线对应函数的解析式；

(2)、判断 $\frac{S_{1}}{S_{2}}$ 是否为定值，如果是，请求出这个定值；如果不是，请说明理由；

(3)、当a取每一个确定的值时，把抛物线y＝ax²+2ax﹣3a向右平移a个单位后，得到函数y₁的图象．当0≤x≤a+1时，结合图象，求y₁的最大值与最小值的平均数（用含a的式子表示）．

查看试题解析

x	…	﹣2	﹣1	0	1	2	…
y＝ax²+bx+c	…	m	0	3	n	3	…