广东省佛山市三水区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-09-23 类型：期末考试

进入出卷网下载

一、单选题

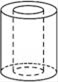
1. 如图是一个空心圆柱体，其俯视图是（）

A、 B、 C、 D、

查看试题解析
2. 方程x²﹣5x＝6的二次项系数、一次项系数、常数项分别是（）

A、1，5，6 B、1，﹣5，6 C、1，﹣5，﹣6 D、﹣1，5，6

查看试题解析
3. 下列各组图形中，一定相似的是（）

A、两个矩形 B、两个菱形 C、两个正方形 D、两个等腰三角形

查看试题解析
4. 顺次连接菱形四边中点得到的四边形一定是（）

A、矩形 B、平行四边形 C、菱形 D、正方形

查看试题解析
5. 已知Rt△ABC中，∠C＝90°，sinA＝ $\frac{5}{13}$ ，BC＝10，则AB等于（）

A、26 B、32 C、24 D、12

查看试题解析
6. 用配方法解方程x²＋10x＋9＝0，变形后的结果正确的是（）

A、（x＋10）²＝9 B、（x＋10）²＝16 C、（x＋5）²＝9 D、（x＋5）²＝16

查看试题解析
7. 已知反比例函数y＝ $\frac{4}{x}$ ，下列结论正确的是（）

A、图象在第二、四象限 B、当x＞0时，函数值y随x的增大而减小 C、图象经过点（﹣2，2） D、图象与x轴的交点为（4，0）

查看试题解析
8. 在1，2，3三个数中任取两个组成一个两位数，则组成的两位数大于15的概率为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
9. 如图，在△ABC中，点D、E分别为AB、AC边上的点，连接DE，且DE∥BC，点F为BC边上一点，连接AF交DE于点G，则下列结论中一定正确的是（）

A、 $\frac{B D}{A B} = \frac{A G}{A F}$ B、 $\frac{A G}{G F} = \frac{D G}{B F}$ C、 $\frac{D G}{B F} = \frac{G E}{F C}$ D、 $\frac{G E}{F C} = \frac{A F}{A G}$

查看试题解析
10. 如图①，在矩形ABCD中，AB＞AD，对角线AC，BD相交于点O，动点P由点A出发，沿A→B→C运动．设点P的运动路程为x，△AOP的面积为y，y与x的函数关系图象如图②所示，则AB边的长为（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

11. 若两个相似三角形的面积比为9：25，则这两个相似三角形的周长比是．

查看试题解析
12. 在一个不透明的袋子中装有3个白球和若干个红球，这些球除颜色外都相同．每次从袋子中随机摸出一个球，记下颜色后再放回袋中，通过多次重复试验发现摸出红球的频率稳定在0.8附近，则袋子中红球约有个．

查看试题解析
13. 已知一元二次方程x²﹣4x＋c＝0无实数根，则c的取值范围是．

查看试题解析
14. 一个菱形的面积为20cm² ，它的两条对角线长分别为ycm，xcm，则y与x之间的函数关系式为y＝．

查看试题解析
15. 如图，在Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线，E、F分别为DB、BC的中点，若AB＝8，则EF＝．

查看试题解析
16. △ABC中，∠A、∠B均为锐角，且（tanA﹣ $\sqrt{3}$ ）²＋|2cosB﹣1|＝0，则△ABC的形状是．

查看试题解析
17. 如图，正方形ABCD的边长为1，点E，F分别为BC，CD边的中点，连接AE，BF交于点P，连接PD，则下述结论：①AE⊥BF；②tan∠DAP＝ $\frac{1}{2}$ ；③DA＝DP；④FD＝FP中，一定成立的有．

查看试题解析

三、解答题

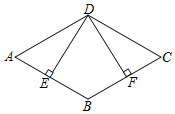
18. 计算：sin30°＋cos45°﹣tan30°•sin60°．

查看试题解析
19. 如图，在菱形ABCD中，过点D分别作DE⊥AB于点E，作DF⊥BC于点F．求证：AE＝CF．

查看试题解析
20. 如图，在平面直角坐标系中，以原点O为位似中心，将△OAB放大到原来的2倍后得到△OA′B′，其中A、B在图中格点上，点A、B的对应点分别为A′、B′．

(1)、在第一象限内画出△OA′B′；

(2)、求△OA′B′的面积．

查看试题解析
21. 为落实“垃圾分类”，环保部门要求垃圾要按A，B，C，D四类分别装袋、投放，其中A类指废电池、过期药品等有毒垃圾，B类指剩余食品等厨余垃圾，C类指塑料、废纸等可回收物，D类指其他垃圾．小明、小亮各自投放了一袋垃圾．

(1)、小明投放的垃圾恰好是C类的概率是；

(2)、求小明投放的垃圾与小亮投放的垃圾是同一类的概率．

查看试题解析
22. 三水大桥是一座横跨北江的特大桥梁，是一座独塔单索面斜拉桥．某无人机兴趣小组为测量主塔顶端A距离水面的高度，在无人机上搭载了测角仪，飞行到C点悬空，测得A点的仰角为30°，测得B点的俯角为22°，已知观测C到主塔的水平距离（CD的长）约为90米，求斜拉索顶端A点到水面B点的距离（AB的长）．（已知 $\sqrt{3}$ ≈1.73，tan22°≈0.40，sin22°≈0.37，cos22°≈0.93，结果精确到0.1）

查看试题解析
23. 一商店销售某种商品，平均每天可售出12件，每件盈利20元．为了扩大销售、增加盈利，该店采取了降价措施，在每件盈利不少于15元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件．

(1)、若每件商品降价2元，则平均每天盈利多少元？

(2)、当每件商品降价多少元时，该商店每天的盈利为320元？

查看试题解析
24. 如图，在第一象限内有一点A（4，1），过点A作AB⊥x轴于B点，作AC⊥y轴于C点，点N为线段AB上的一动点，过点N的反比例函数y＝ $\frac{n}{x}$ 交线段AC于M点，连接OM，ON，MN．

(1)、若点N为AB的中点，则n的值为；

(2)、求线段AN的长（用含n的代数式表示）；

(3)、求△AMN的面积等于 $\frac{1}{4}$ 时n的值．

查看试题解析
25. 如图①，已知Rt△ABC中，∠C＝90°，AC＝8cm，BC＝6cm，点P由B出发沿BA方向向点A匀速运动，同时点Q由A出发沿AC方向向点C匀速运动，它们的速度均为2cm/s．以AQ、PQ为边作▱AQPD，连接DQ，交AB于点E．设运动时间为t（单位：s）（0≤t≤4）．解答下列问题：

(1)、当t为何值时，AQ＝AP；

(2)、如图②，当t为何值时，▱AQPD为矩形；

(3)、当t为何值时，△PEQ是以PE为直角边的直角三角形．

查看试题解析