广东省佛山市南海区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-23 类型:期末考试
一、单选题
-
1. 抛物线y=(x+2)2+3的顶点坐标是( )A、(﹣2,﹣3) B、(﹣2,3) C、(2,﹣3) D、(2,3)2. 用配方法解方程 时,配方后所得的方程为( )A、 B、 C、 D、3. 班级元旦晚会上,主持人给大家带来了一个有奖竞猜题,他在一个不透明的袋子中放了若干个形状大小完全相同的白球,想请大家估计出袋中白球的个数.数学科代表小明是这样来估计的:他先往袋中放入10个形状大小与白球相同的红球,混匀后再从袋子中随机摸出20个球,发现其中有4个红球.根据小明的方法估计袋中白球有( )A、200个 B、100个 C、50个 D、40个4. 如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC与△ADE相似的是( )
 A、∠C=∠AED B、∠B=∠D C、 D、5. 如图所示几何体的左视图正确的是( )
A、∠C=∠AED B、∠B=∠D C、 D、5. 如图所示几何体的左视图正确的是( )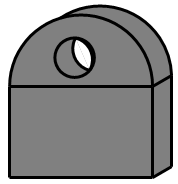 A、
A、 B、
B、 C、
C、 D、
D、 6. 点A(﹣3,y1)、B(﹣1,y2)、C(2,y3)都在反比例函数y= 的图象上,则y1、y2、y3的大小关系是( )A、y1 y2 y3 B、y3 y2 y1 C、y3 y1 y2 D、y2 y1 y37. 已知四边形 中,对角线 , 相交于点 ,且 ,则下列关于四边形 的结论一定成立的是( )A、四边形 是正方形 B、四边形 是菱形 C、四边形 是矩形 D、8. 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,BC= ,AC=3,则sin∠ACD=( )
6. 点A(﹣3,y1)、B(﹣1,y2)、C(2,y3)都在反比例函数y= 的图象上,则y1、y2、y3的大小关系是( )A、y1 y2 y3 B、y3 y2 y1 C、y3 y1 y2 D、y2 y1 y37. 已知四边形 中,对角线 , 相交于点 ,且 ,则下列关于四边形 的结论一定成立的是( )A、四边形 是正方形 B、四边形 是菱形 C、四边形 是矩形 D、8. 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,BC= ,AC=3,则sin∠ACD=( ) A、 B、 C、 D、9. 二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 与正比例函数y=cx在同一坐标系内的大致图象是( )
A、 B、 C、 D、9. 二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 与正比例函数y=cx在同一坐标系内的大致图象是( ) A、
A、 B、
B、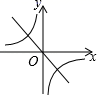 C、
C、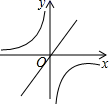 D、
D、 10. 如图,在△ABC中,中线AE、BD相交于点F , 连接DE , 则下列结论:① ;② ;③ ;④ .其中正确结论的个数是( )
10. 如图,在△ABC中,中线AE、BD相交于点F , 连接DE , 则下列结论:① ;② ;③ ;④ .其中正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 一元二次方程 的解为.12. 已知 ,则 = .13. 直角三角形两直角边长分别为5cm和12cm,则斜边上的中线长为cm.14. 某市推出名师网络课堂,据统计,第一批受益学生8000人次,第三批受益学生18000人次.如果第二批、第三批受益学生人次的平均增长率相同,则这个增长率为 .15. 如图,测角仪CD竖直放在距建筑物AB底部8m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪CD的高度是1.5m , 则建筑物AB的高度约为m . (结果精确到个位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
 16. 在研究:“任意给定一个矩形A , 是否存在另一个矩形B , 它的周长和面积分别是已知矩形周长和面积的一半”时,小明发现:当已知矩形A的长和宽分别为6和1时,存在一个矩形B的周长和面积分别是矩形A周长和面积的一半,那么矩形B的长为 .17. 如图,在菱形ABCD中,AB=1,∠ADC=120°,以AC为边作菱形ACC1D1 , 且∠AD1C1=120°;再以AC1为边作菱形AC1C2D2 , 且∠AD2C2=120°…;按此规律,菱形AC2020C2021D2021的面积为 .
16. 在研究:“任意给定一个矩形A , 是否存在另一个矩形B , 它的周长和面积分别是已知矩形周长和面积的一半”时,小明发现:当已知矩形A的长和宽分别为6和1时,存在一个矩形B的周长和面积分别是矩形A周长和面积的一半,那么矩形B的长为 .17. 如图,在菱形ABCD中,AB=1,∠ADC=120°,以AC为边作菱形ACC1D1 , 且∠AD1C1=120°;再以AC1为边作菱形AC1C2D2 , 且∠AD2C2=120°…;按此规律,菱形AC2020C2021D2021的面积为 .
三、解答题
-
18. 计算:6sin30°﹣ cos30°﹣2tan45°+ .19. “一方有难,八方支援”2020年初武汉受到新型冠状肺炎影响,南海区某医院准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士支援武汉.(1)、若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果;(2)、求恰好选中医生丙和护士B的概率.20. 如图,已知AB CD , AD , BC交于点E , F为BC上一点,且∠EAF=∠C , 若AF=6,FB=8,求EF .
 21. 已知关于x的方程 .(1)、当该方程的一个根为1时,求a的值及该方程的另一根;(2)、求证:不论a取何实数,该方程都有两个不相等的实数根.22. 如图,已知一次函数y=ax+b与反比例函数 的图象相交于点A(1,3)和B(m , 1).
21. 已知关于x的方程 .(1)、当该方程的一个根为1时,求a的值及该方程的另一根;(2)、求证:不论a取何实数,该方程都有两个不相等的实数根.22. 如图,已知一次函数y=ax+b与反比例函数 的图象相交于点A(1,3)和B(m , 1). (1)、求反比例函数与一次函数的表达式;(2)、根据图象回答,当x取何值时,反比例函数的值大于一次函数的值;(3)、以点O为位似中心画三角形,使它与△OAB位似,且相似比为2,请在图中画出所有符合条件的三角形.23. 如图,BD是△ABC的角平分线,过点作DE BC交AB于点E , DF AB交BC于点F .
(1)、求反比例函数与一次函数的表达式;(2)、根据图象回答,当x取何值时,反比例函数的值大于一次函数的值;(3)、以点O为位似中心画三角形,使它与△OAB位似,且相似比为2,请在图中画出所有符合条件的三角形.23. 如图,BD是△ABC的角平分线,过点作DE BC交AB于点E , DF AB交BC于点F . (1)、求证:四边形BEDF是菱形;(2)、若∠ABC=60°,∠ACB=45°,CD=6,求菱形BEDF的边长.24. 如图1,在△ABC中,∠A=90°,AB=6,AC=8,点D , F分别是边AB , BC上的动点,点D不与点A , B重合,过点D作DE BC , 交AC于点E , 连接DF , EF .
(1)、求证:四边形BEDF是菱形;(2)、若∠ABC=60°,∠ACB=45°,CD=6,求菱形BEDF的边长.24. 如图1,在△ABC中,∠A=90°,AB=6,AC=8,点D , F分别是边AB , BC上的动点,点D不与点A , B重合,过点D作DE BC , 交AC于点E , 连接DF , EF . (1)、当DF⊥BC时,求证:△FBD∽△ABC;(2)、在(1)的条件下,当四边形BDEF是平行四边形时,求BF的长;(3)、是否存在点F , 使得△FDE为等腰直角三角形?若不存在,请说明理由;若存在,请求出DE的长.25. 如图,已知二次函数y=ax2﹣5ax+2的图象交x轴于点A(1,0)和点B , 交y轴于点C .
(1)、当DF⊥BC时,求证:△FBD∽△ABC;(2)、在(1)的条件下,当四边形BDEF是平行四边形时,求BF的长;(3)、是否存在点F , 使得△FDE为等腰直角三角形?若不存在,请说明理由;若存在,请求出DE的长.25. 如图,已知二次函数y=ax2﹣5ax+2的图象交x轴于点A(1,0)和点B , 交y轴于点C . (1)、求该二次函数的解析式;(2)、过点A作y轴的平行线,点D在这条直线上且纵坐标为3,求∠CBD的正切值;(3)、在(2)的条件下,点E在直线x=1上,如果∠CBE=45°,求点E的坐标.
(1)、求该二次函数的解析式;(2)、过点A作y轴的平行线,点D在这条直线上且纵坐标为3,求∠CBD的正切值;(3)、在(2)的条件下,点E在直线x=1上,如果∠CBE=45°,求点E的坐标.