广东省东莞市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-09-23 类型:期末考试
一、单选题
-
1. 下列图形中不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知,⊙O的半径为5cm,点P到圆心O的距离为4cm,则点P在⊙O的( )A、外部 B、内部 C、圆上 D、不能确定3. 抛物线y= x2向左平移1个单位,再向上平移2个单位后,所得抛物线的表达式是( )A、y= (x+1)2﹣2 B、y= (x﹣1)2+2 C、y= (x﹣1)2﹣2 D、y= (x+1)2+24. 有6张扑克牌面数字分别是3,4,5,7,8,10从中随机抽取一张点数为偶数的概率是( )A、 B、 C、 D、5. 下列事件中,属于必然事件的是( )A、小明买彩票中奖 B、投掷一枚质地均匀的骰子,掷得的点数是奇数 C、等腰三角形的两个底角相等 D、 是实数,6. 已知一元二次方程 有一个根为2,则另一个根为( )A、10 B、6 C、8 D、-27. 如图, 是 的直径,弦 于点 , , 的半径为 ,则 弦长为( )
2. 已知,⊙O的半径为5cm,点P到圆心O的距离为4cm,则点P在⊙O的( )A、外部 B、内部 C、圆上 D、不能确定3. 抛物线y= x2向左平移1个单位,再向上平移2个单位后,所得抛物线的表达式是( )A、y= (x+1)2﹣2 B、y= (x﹣1)2+2 C、y= (x﹣1)2﹣2 D、y= (x+1)2+24. 有6张扑克牌面数字分别是3,4,5,7,8,10从中随机抽取一张点数为偶数的概率是( )A、 B、 C、 D、5. 下列事件中,属于必然事件的是( )A、小明买彩票中奖 B、投掷一枚质地均匀的骰子,掷得的点数是奇数 C、等腰三角形的两个底角相等 D、 是实数,6. 已知一元二次方程 有一个根为2,则另一个根为( )A、10 B、6 C、8 D、-27. 如图, 是 的直径,弦 于点 , , 的半径为 ,则 弦长为( )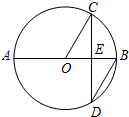 A、 B、 C、 D、8. 若关于 的一元二次方程 有实数根,则字母 的取值范围是( )A、 且 B、 C、 D、 且9. 下列说法错误的是( )A、等弧所对的弦相等 B、圆的内接平行四边形是矩形 C、 的圆周角所对的弦是直径 D、平分一条弦的直径也垂直于该弦10. 如果 ,那么二次函数 的图象大致是( )A、
A、 B、 C、 D、8. 若关于 的一元二次方程 有实数根,则字母 的取值范围是( )A、 且 B、 C、 D、 且9. 下列说法错误的是( )A、等弧所对的弦相等 B、圆的内接平行四边形是矩形 C、 的圆周角所对的弦是直径 D、平分一条弦的直径也垂直于该弦10. 如果 ,那么二次函数 的图象大致是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 方程(x-1)(x+2)=0的两根分别为.12. 在一个不透明的盒子中装有2个白球,n个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是黄球的概率为 ,则n= .13. 在半径为6的圆中,一个扇形的圆心角是120°,则这个扇形的弧长等于 .14. 如果 是一元二次方程 的一个根,那么 的值是 .15. 烟花厂为国庆70周年庆祝晚会特别设计制作一种新型礼炮,这种礼炮的升空高h(m)与飞行时间t(s)的关系式是 ,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要时间为.16. 如图,将△ABC绕点 旋转到△AEF的位置,点E在BC边上,EF与AC交于点G.若∠B=70°,∠C=25°,则∠FGC=°.
 17. 如图,等边三角形 中,点 是 的中心, ,绕点 旋转 ,分别交线段 、 于 、 两点,连接 ,给出下列四个结论:① ;② ;③四边形 的面积始终等于定值;④当 时, 周长最小.上述结论中正确的有(写出序号).
17. 如图,等边三角形 中,点 是 的中心, ,绕点 旋转 ,分别交线段 、 于 、 两点,连接 ,给出下列四个结论:① ;② ;③四边形 的面积始终等于定值;④当 时, 周长最小.上述结论中正确的有(写出序号).
三、解答题
-
18. 解方程: .19. 方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后, 的顶点均在格点上.
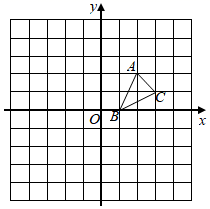 (1)、画出 绕 点顺时针旋转 后的 ,并写出 的坐标;(2)、画出 关于原点 对称的 .20. 已知抛物线 经过点 和点 .
(1)、画出 绕 点顺时针旋转 后的 ,并写出 的坐标;(2)、画出 关于原点 对称的 .20. 已知抛物线 经过点 和点 .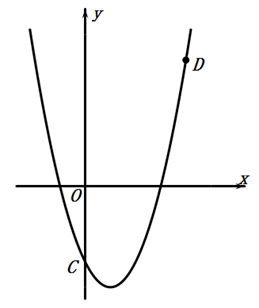 (1)、求抛物线的解析式;(2)、设抛物线与 轴的交点 、 的坐标(注:点 在点 的左边),求 的面积.21. 小李和小王两位同学做游戏,在一个不透明的口袋中放入1个红球、2个白球、1个黑球,这些球除颜色外都相同,将球摇匀.(1)、从中任意摸出1个球,恰好摸到红球的概率是多少?(2)、两人约定:从袋中一次摸出两个球,若摸出的两个球是-红一黑,则小李获胜:若摸出的两个球都是白色,则小王获胜,请用列举法(画树状图或列表)分析游戏规则是否公平.22. 如图,已知AB是⊙O的直径,C,D是⊙O上的点, ,交AD于点E,连结BC.
(1)、求抛物线的解析式;(2)、设抛物线与 轴的交点 、 的坐标(注:点 在点 的左边),求 的面积.21. 小李和小王两位同学做游戏,在一个不透明的口袋中放入1个红球、2个白球、1个黑球,这些球除颜色外都相同,将球摇匀.(1)、从中任意摸出1个球,恰好摸到红球的概率是多少?(2)、两人约定:从袋中一次摸出两个球,若摸出的两个球是-红一黑,则小李获胜:若摸出的两个球都是白色,则小王获胜,请用列举法(画树状图或列表)分析游戏规则是否公平.22. 如图,已知AB是⊙O的直径,C,D是⊙O上的点, ,交AD于点E,连结BC. (1)、求证:AE=ED;(2)、若AB=6,∠CBD=30°,求图中阴影部分的面积.23. 某地区2018年投入教育经费2000万元,2020年投入教育经费2880万元.(1)、求2018年至2020年该地区投入教育经费的年平均增长率;(2)、根据(1)所得的年平均增长率,预计2021年该地区将投入教育经费多少万元.
(1)、求证:AE=ED;(2)、若AB=6,∠CBD=30°,求图中阴影部分的面积.23. 某地区2018年投入教育经费2000万元,2020年投入教育经费2880万元.(1)、求2018年至2020年该地区投入教育经费的年平均增长率;(2)、根据(1)所得的年平均增长率,预计2021年该地区将投入教育经费多少万元.

