重庆市西北狼教育联盟2021-2022学年高二上学期数学开学质量检测试卷
试卷更新日期:2021-09-23 类型:开学考试
一、单选题
-
1. 已知复数 (i是虚数单位)是纯虚数,则实数 ( )A、-2 B、-1 C、0 D、12. 已知单位向量 , ,满足 ,则 与 夹角的余弦值为( )A、 B、 C、 D、3. 在△ABC中,若(a+c)(a-c)=b(b-c),则A等于( )A、90° B、60° C、120° D、150°4. 古代将圆台称为“圆亭”,《九章算术》中“今有圆亭,下周三丈,上周二丈,高一丈,问积几何?”即一圆台形建筑物,下底周长3丈,上底周长2丈,高1丈,则它的体积为( )A、 立方丈 B、 立方丈 C、 立方丈 D、 立方丈5. 已知甲、乙两组数据(已按从小到大的顺序排列):甲组:27,28,39,40,m,50;乙组:24,n,34,43,48,52.若这两组数据的30百分位数、80百分位数分别相等,则 等于( )A、 B、 C、 D、6. 袋子里有4个大小、质地完全相同的球,其中有2个红球、2个白球,从中不放回地依次随机摸出2个球,事件 “两个球颜色相同”,事件 “两个球颜色不同”,事件 “第二次摸到红球”,事件 “两个球都是红球”.下列说法错误的是( )A、 B、C与D互斥 C、 D、7. 在正方体 中,三棱锥 的表面积为 ,则正方体外接球的体积为( )A、 B、 C、 D、8. 中,角A,B,C的对边分别是a,b,c,已知 ,则A=( )A、 B、 C、 D、
二、多选题
-
9. 已知m , n是两条不重合的直线, , 是两个不重合的平面,则( )A、若 , ,则 B、若 , ,则 C、若 , , ,则 D、若 , , ,则10. 2020年新型冠状病毒肺炎疫情对消费饮食行业造成了很大影响,为了解A、B两家大型餐饮店受影响的程度,现统计了2020年2月到7月A、B两店每月营业额,得到如图所示的折线图,根据营业额折线图,下列说法正确的是( )
 A、A店营业额的极差比B店营业额的极差小 B、A店2月到7月营业额的75%分位数是45 C、B店2月到7月每月增加的营业额越来越多 D、B店2月到7月的营业额的平均值为2911. 以下关于正余弦定理或其变形正确的有( )A、在 中, B、在 中,若 ,则 C、在 中,若 ,则 ,若 ,则 都成立 D、在 中,三个内角A , B , C的对边分别为a , b , c , 且 , ,则12. 已知点O为 所在平面内一点,且 ,则下列选项正确的是( )A、 B、直线 必过 边的中点 C、 D、若 ,且 ,则
A、A店营业额的极差比B店营业额的极差小 B、A店2月到7月营业额的75%分位数是45 C、B店2月到7月每月增加的营业额越来越多 D、B店2月到7月的营业额的平均值为2911. 以下关于正余弦定理或其变形正确的有( )A、在 中, B、在 中,若 ,则 C、在 中,若 ,则 ,若 ,则 都成立 D、在 中,三个内角A , B , C的对边分别为a , b , c , 且 , ,则12. 已知点O为 所在平面内一点,且 ,则下列选项正确的是( )A、 B、直线 必过 边的中点 C、 D、若 ,且 ,则三、填空题
-
13. 已知向量 , , .若向量 与向量 共线,则实数 .14. 如图,正方体 中,EF , 分别为棱 , 的中点,则异面直线 与 所成角的余弦值是.
 15. 一个三位自然数百位,十位,个位上的数字依次为a , b , c , 当且仅当a>b , b<c时称为“凹数”如213),若 ,且a , b , c互不相同,则这个三位数为“凹数”的概率为 .16. 在锐角 中,内角A , B , C的对边分别为a , b , c , 已知 且, ,则 的面积的取值范围是.
15. 一个三位自然数百位,十位,个位上的数字依次为a , b , c , 当且仅当a>b , b<c时称为“凹数”如213),若 ,且a , b , c互不相同,则这个三位数为“凹数”的概率为 .16. 在锐角 中,内角A , B , C的对边分别为a , b , c , 已知 且, ,则 的面积的取值范围是.四、解答题
-
17. 某城市100户居民的月平均用电量(单位:度),以 , , , , , , 分组的频率分布直方图如图.
 (1)、求直方图中x的值;(2)、求月平均用电量的众数和中位数;(3)、在月平均用电量为 , , , 的四组用户中,用分层抽样的方法抽取
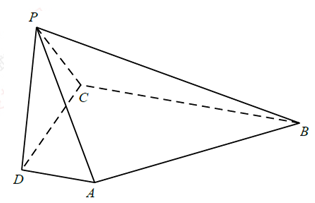
(1)、求直方图中x的值;(2)、求月平均用电量的众数和中位数;(3)、在月平均用电量为 , , , 的四组用户中,用分层抽样的方法抽取 户居民,则月平均用电量在 的用户中应抽取多少户? 18. 请从下面三个条件中任选一个,补充在下面的横线上,并作答.① ;② ;③ 的面积为 .已知 的内角 , , 的对边分别为 , , ,且 .(1)、求 ;(2)、若 为 中点,且 , ,求 , .19. 三棱锥 中,平面 平面 , 为等边三角形, 且 , 、 分别为 、 的中点.
户居民,则月平均用电量在 的用户中应抽取多少户? 18. 请从下面三个条件中任选一个,补充在下面的横线上,并作答.① ;② ;③ 的面积为 .已知 的内角 , , 的对边分别为 , , ,且 .(1)、求 ;(2)、若 为 中点,且 , ,求 , .19. 三棱锥 中,平面 平面 , 为等边三角形, 且 , 、 分别为 、 的中点. (1)、求证: 平面 ;(2)、求证:平面 平面 ;(3)、求三棱锥 的体积.20. 西北狼联盟”学校为了让同学们树立自己的学习目标,特进行了“生涯规划”知识竞赛.已知甲、乙两队参赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为 ,乙队中3人答对的概率分别为 , , ,且各人回答正确与否相互之间没有影响.(1)、分别求甲队总得分为0分;2分的概率;(2)、求甲队得2分乙队得1分的概率.
(1)、求证: 平面 ;(2)、求证:平面 平面 ;(3)、求三棱锥 的体积.20. 西北狼联盟”学校为了让同学们树立自己的学习目标,特进行了“生涯规划”知识竞赛.已知甲、乙两队参赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为 ,乙队中3人答对的概率分别为 , , ,且各人回答正确与否相互之间没有影响.(1)、分别求甲队总得分为0分;2分的概率;(2)、求甲队得2分乙队得1分的概率.