辽宁省六校2021-2022学年高二上学期数学期初联考试卷

试卷更新日期：2021-09-23 类型：开学考试

进入出卷网下载

一、单选题

1. 复数 $\frac{{(1 - i)}^{2}}{1 + i} =$ （）

A、 $1 - i$ B、 $- 1 - i$ C、 $1 + i$ D、 $- 1 + i$

查看试题解析
2. 设 $△ A B C$ 内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，且 $b = \sqrt{2}$ ， $c = \sqrt{3}$ ， $C = 60 °$ ，则角 $B =$ （）

A、 $45 °$ B、 $30 °$ C、 $45 °$ 或 $135 °$ D、 $30 °$ 或 $150 °$

查看试题解析
3.
已知非零向量 $\vec{a}$ ， $\vec{b}$ 满足| $\vec{b}$ |=4| $\vec{a}$ |，且 $\vec{a}$ ⊥（2 $\vec{a}$ + $\vec{b}$ ），则 $\vec{a}$ 与 $\vec{b}$ 的夹角为（）

A、 $\frac{π}{3}$ B、 $\frac{π}{2}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
4. 某校高一 (1)班甲、乙两同学进行投篮比赛，他们进球的概率分别是 $\frac{2}{3}$ 和 $\frac{3}{5}$ ，现甲、乙各投篮一次，至少有一人投进球的概率是（）

A、 $\frac{2}{5}$ B、 $\frac{7}{15}$ C、 $\frac{2}{15}$ D、 $\frac{13}{15}$

查看试题解析
5. 已知两条不同的直线 $l ， m$ 和两个不同的平面 $α ， β$ ，下列四个命题中错误的为（）

A、若 $m ⊥ β$ ， $n ⊥ β$ ， $n ⊥ α$ ，则 $m ⊥ α$ B、若 $m // β$ ， $β ⊥ α$ ，则 $m ⊥ α$ C、若 $α \cap β = m$ ， $l // α$ 且 $l // β$ ，则 $l // m$ D、若 $α / / β ， m \subset α$ ，那么 $m / / β$

查看试题解析
6. 已知 $f (x)$ 是定义域为 $R$ 的奇函数，当 $x > 0$ 时， $f (x) = x^{2} - 2 x - 3$ ，则不等式 $f (x + 2) < 0$ 的解集是（）

A、 $(- 5 ， - 2) \cup (- 2 ， 1)$ B、 $(- \infty ， - 5) \cup (- 2 ， 1)$ C、 $(- 5 ， - 2) \cup (1 ， + \infty)$ D、 $(- \infty ， - 1) \cup (2 ， 5)$

查看试题解析
7. 已知 $α \in (- \frac{π}{2} ， 0)$ ， $\cos (α - \frac{π}{2}) = - \frac{3}{5}$ ，则 $\sin 2 α =$ （）

A、 $\frac{1}{25}$ B、 $\frac{24}{25}$ C、 $- \frac{24}{25}$ D、 $- \frac{1}{25}$

查看试题解析
8. 在 $△ A B C$ 中，角A， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，且 $2 c \cos B = 2 a + b$ ，若 $△ A B C$ 的面积 $S = \frac{\sqrt{3}}{12} c$ ，则 $a b$ 的最小值为（）

A、 $\frac{1}{3}$ B、3 C、 $\frac{1}{2}$ D、 $\frac{1}{6}$

查看试题解析

二、多选题

9. 如果一个复数的实部和虚部相等，则称这个复数为“等部复数”．若复数 $z = a + i$ （ $a \in R$ ， $i$ 为虚数单位）为“等部复数”，则下列说法正确的是（）

A、 $a = 1$ B、 $| z | = 1$ C、 $\bar{z} = 1 - i$ D、复数 $(a - 1) + (a^{2} - 1) i$ 是纯虚数

查看试题解析
10. 若 $a > 0$ ， $b > 0$ ，且 $a + b = 2$ ，则下列不等式恒成立的是（）

A、 $\sqrt{a b} \geq 1$ B、 $\frac{1}{a b} \geq 1$ C、 $a^{2} + b^{2} \geq 2$ D、 $\frac{1}{a} + \frac{1}{b} \geq 2$

查看试题解析
11. 下列结论正确的是（）

A、在 $△ A B C$ 中， $A > B$ 是 $\sin A > \sin B$ 充要条件 B、在 $△ A B C$ 中， $2 \cos B \sin A = \sin C$ ，则 $△ A B C$ 为等腰三角形 C、在 $△ A B C$ 中， $a \cos A = c \cos C$ ，则 $△ A B C$ 为等腰三角形 D、在 $△ A B C$ 中， $b^{2} = a c$ ，且 $2 \sin B = \sin A + \sin C$ ，则 $△ A B C$ 为正三角形

查看试题解析
12. 《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”；底面为矩形，一条侧棱垂直于底面的四棱锥称之为“阳马”；四个面均为直角三角形的四面体称为“鳖臑”.如图在堑堵ABC-A₁B₁C₁中，AC⊥BC，且 AA₁=AB=2.下列说法正确的是

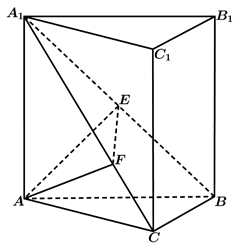A、四棱锥B-A₁ACC₁为“阳马” B、四面体A₁C₁CB为“鳖臑” C、四棱锥B-A₁ACC₁体积最大为 $\frac{2}{3}$ D、过A点分别作AE⊥A₁B于点E，AF⊥A₁C于点F，则EF⊥A₁B

查看试题解析

三、填空题

13. 已知 $\vec{a} = (- 1 ， 2)$ ， $\vec{b} = (3 ， - 1)$ ，则与 $\vec{a} - \vec{b}$ 同方向的单位向量是．

查看试题解析
14. 已知函数 $f (2 x - 1) = 3 x - 5$ ，若 $f (x_{0}) = 4$ ，则 $x_{0} =$ .

查看试题解析
15. 当 $x = θ$ 时，函数 $f (x) = \sin x - 2 \cos x (x \in R)$ 取得最大值，则 $\cos θ + 2 \sin θ =$ .

查看试题解析
16. 若三棱锥S-ABC的所有顶点都在球O的球面上，SA⊥平面ABC ， SA= $3$ ， $B C = 2 \sqrt{2}$ ， $∠ B A C = 45 °$ 则球O的表面积

查看试题解析

四、解答题

17. 已知向量 $\overset{⇀}{a} = (2 \cos θ ， \sin θ) ， \overset{⇀}{b} = (1 ， - 2)$ .

(1)、若 $\overset{⇀}{a} / / \overset{⇀}{b}$ ，求 $\frac{3 \sin θ - 2 \cos θ}{2 \sin θ + \cos θ}$ 的值；

(2)、若 $θ = 45^{\circ} ， 2 \overset{⇀}{a} - t \overset{⇀}{b}$ 与 $\sqrt{2} \overset{⇀}{a} + \overset{⇀}{b}$ 垂直，求实数 $t$ 的值.

查看试题解析
18. 已知函数 $f (x) = A \cos (ω x + φ) + B (A > 0 ， ω > 0 ， | φ | < \frac{π}{2})$ 的部分图象，如图所示.

(1)、求函数 $f (x)$ 的解析式；

(2)、先将函数 $f (x)$ 图象上所有点的横坐标缩短到原来的 $\frac{1}{2}$ （纵坐标不变），再向右平移 $\frac{π}{6}$ 个单位后得到函数 $g (x)$ 的图象，求函数 $y = g (x)$ 的单调减区间和在区间 $[0 ， \frac{π}{4}]$ 上的最值.

查看试题解析
19. 在四棱锥 $P - A B C D$ 中，四边形 $A B C D$ 为正方形，平面 $P A B ⊥$ 平面 $A B C D ， △ P A B$ 为等腰直角三角形， $P A ⊥ P B ， A B = 2$ ．

(1)、求证：平面 $P B C ⊥$ 平面 $P A C$ ；

(2)、设 $E$ 为 $C D$ 的中点，求点 $E$ 到平面 $P B C$ 的距离．

查看试题解析
20. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 的对边分别是 $a$ ， $b$ ， $c$ ， $(2 a - c) \cos B = b \cdot \cos C$ .

(1)、求角 $B$ 的大小；

(2)、若 $a = 3$ ， $b = \sqrt{19}$ ，点 $D$ 在边 $A C$ 上，且 $A D = 2 D C$ ，求 $B D$ 的长度.

查看试题解析
21. 如图，四棱锥 $P - A B C D$ 中，平面 $P B C ⊥$ 平面 $A B C D$ ， $∠ P B C = 90 °$ ， $A D / / B C$ ， $∠ A B C = 90 °$ ， $2 A B = 2 A D = \sqrt{2} C D = B C = 2$

(1)、求证： $C D ⊥$ 平面 $P B D$ ；

(2)、若直线 $P D$ 与底面 $A B C D$ 所成的角的余弦值为 $\frac{\sqrt{3}}{3}$ ，求二面角 $B - P C - D$ 的余弦值.

查看试题解析
22. 已知定义域为 $R$ 的函数 $f (x) = \frac{n - 3^{x}}{3 + 3^{x + 1}}$ 是奇函数.

(1)、求 $y = f (x)$ 的解析式；

(2)、若 $f (\log_{4} x \cdot \log_{2} \frac{8}{x}) + f (4 - 2 a) > 0$ 恒成立，求实数 $a$ 的取值范围.

查看试题解析