备考2022年中考数学一轮复习（湘教版）专题67 数据的分析
试卷更新日期：2021-09-23 类型：一轮复习
一、单选题
-
1. 某校九年级进行了3次数学模拟考试，甲、乙、丙三名同学的平均分为及方差 如右表所示，那么这三名同学数学成绩最稳定的是（ ）
甲
乙
丙
91
91
91
6
24
54
A、甲 B、乙 C、丙 D、无法确定2. 甲、乙、丙、丁四人10次随堂测验的成绩如图所示，从图中可以看出这10次测验平均成绩较高且较稳定的是（ ）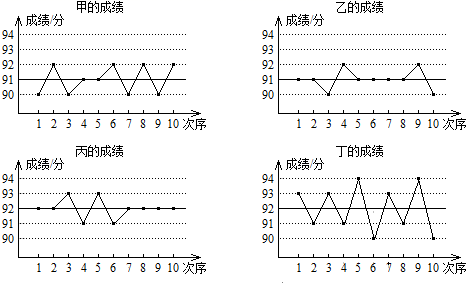
A、甲 B、乙 C、丙 D、丁3. 全民反诈，刻不容缓！陈科同学参加学校举行的“防诈骗”主题演讲比赛，五位评委给出的分数分别为90，80，86，90，94，则这组数据的中位数和众数分别是（ ）A、80，90 B、90，90 C、86，90 D、90，944. 为了向建党一百周年献礼，我市中小学生开展了红色经典故事演讲比赛.某参赛小组6名同学的成绩（单位：分）分别为：85，82，86，82，83，92.关于这组数据，下列说法错误的是（ ）A、众数是82 B、中位数是84 C、方差是84 D、平均数是855. 小明收集了鄂尔多斯市某酒店2021年3月1日～3月6日每天的用水量（单位：吨），整理并绘制成如图所示的折线统计图，下列结论正确的是（ ）
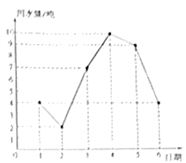A、平均数是 B、众数是10 C、中位数是8.5 D、方差是6. 某校健美操队共有10名队员，统计队员的年龄情况，结果如下：13岁3人，14岁5人，15岁2人该健美操队队员的平均年龄为（ ）A、14.2岁 B、14.1岁 C、13.9岁 D、13.7岁7. 一组数据：2，4，4，4，6，若去掉一个数据4，则下列统计量中发生变化的是（ ）A、众数 B、中位数 C、平均数 D、方差8. 为迎接中国共产党建党一百周年，某班50名同学进行了党史知识竞赛，测试成绩统计如下表，其中有两个数据被遮盖．成绩/分
91
92
93
94
95
96
97
98
99
100
人数
■
■
1
2
3
5
6
8
10
12
下列关于成绩的统计量中，与被遮盖的数据无关的是（ ）
A、平均数，方差 B、中位数，方差 C、中位数，众数 D、平均数，众数9. 一组数据：3，4，4，4，5，若去掉一个数据4，则下列统计量中发生变化的是（ ）A、众数 B、中位数 C、平均数 D、方差10. 为了保护环境加强环保教育，某中学组织学生参加义务收集废旧电池的活动，下面是随机抽取40名学生对收集废旧电池的数量进行的统计：废旧电池数/节
4
5
6
7
8
人数/人
9
11
11
5
4
请根据学生收集到的废旧电池数，判断下列说法正确的是（ ）
A、样本为40名学生 B、众数是11节 C、中位数是6节 D、平均数是5.6节二、填空题
-
11. 为庆祝中国共产党建党一百周年，某校开展了主题为“我身边的共产党员”的演讲比赛.比赛从演讲内容、演讲技巧、演讲效果三个方面打分，最终得分按4：3：3的比例计算.若选手甲在演讲内容、演讲技巧、演讲效果三个方面的得分分别为95分、80分、90分，则选手甲的最终得分为 分.12. 为了庆祝中国共产党成立100周年，某校举行“党在我心中”演讲比赛，评委将从演讲内容，演讲能力，演讲效果三个方面给选手打分，各项成绩均按百分制计，然后再按演讲内容占50%，演讲能力占40%，演讲效果占10%，计算选手的综合成绩（百分制）.小婷的三项成绩依次是84，95，90，她的综合成绩是.13. 某外贸公司要出口一批规格为 克/盒的红枣，现有甲、乙两个厂家提供货源，它们的价格相同，品质也相近.质检员从两厂的产品中各随机抽取 盒进行检测，测得它们的平均质量均为 克，每盒红枣的质量如图所示，则产品更符合规格要求的厂家是.（填“甲”或“乙”）
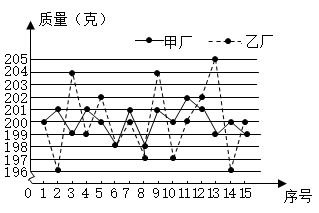14. 甲乙两班举行一分钟跳绳比赛，参赛学生每分钟跳绳次数的统计结果如表：班级
参加人数
中位数
方差
平均数
甲
45
109
181
110
乙
45
111
108
110
某同学分析如表后得到如下结论：①甲，乙两班学生平均成绩相同；②乙班优秀人数多于甲班优秀人数（每分钟跳绳≥110次为优秀）；③甲班成绩的波动比乙班大，则正确结论的序号是 ．
15. 在某次体育测试中，甲、乙两班成绩的平均数、中位数、方差如下表所示，规定学生个人成绩大于90分为优秀，则甲、乙两班中优秀人数更多的是班.人数
平均数
中位数
方差
甲班
45
82
91
19.3
乙班
45
87
89
5.8
16. 现有甲、乙两种糖果的单价与千克数如下表所示甲种糖果
乙种糖果
单价(元/千克)
30
20
千克数
2
3
将这2千克甲种糖果盒3千克乙种糖果混合成5千克什锦糖果，若商家用加权平均数来确定什锦糖果的单价，则这5千克什锦糖果的单价为元/千克
17. 已知一组数据0，1，x，3，6的平均数是y，则y关于x的函数解析式是 ．18. 某人5次射击命中的环数分别为5，10，7，x ， 10，若这组数据的中位数为8，则这组数据的方差为 ．19. 有甲､乙两组数据，如表所示：甲
11
12
13
14
15
乙
12
12
13
14
14
甲､乙两组数据的方差分别为 ，则 （填“＞”，“＜”或“＝”）．
20. 某学校八年级（2）班有20名学生参加学校举行的“学党史、看红书”知识竞赛，成绩统计如图．这个班参赛学生的平均成绩是 ．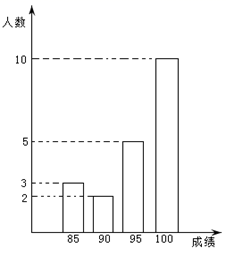
三、解答题
-
21. 某校20名男子足球运动员的年龄情况如下表：
年龄/岁
14
15
16
17
人数
5
7
5
3
请根据表中的数据，求该20名足球运动员的年龄的众数、中位数和平均数．
22. 阅读后填空：某家灯具厂为了比较甲、乙两种灯的使用寿命，各抽出8支做试验，结果如下（单位：小时）．甲：457，438，460，443，464，459，444，451；
乙：466，455，467，439，459，452，464，438．
试说明哪种灯的使用寿命长？哪种灯的质量比较稳定？
23. 我校为了纪念“一二•九”举办了八年级红歌合唱比赛，为了保证这次比赛的公正性，规定：参赛班级的基本素养、精神面貌、服装三项打分分别按5：3：2的比例计入总评成绩．二班、三班、五班的基本素养、精神面貌、服装的打分如下表，计算哪个班是第一名？基本素养
精神面貌
服装
二班
90
96
93
三班
90
90
96
五班
96
94
90
四、综合题
-
24. 某校将学生体质健康测试成绩分为 ， ， ， 四个等级，依次记为4分，3分，2分，1分.为了解学生整体体质健康状况，拟抽样进行统计分析.(1)、以下是两位同学关于抽样方案的对话：
小红：“我想随机柚取七年级男、女生各60人的成绩.”
小明：“我想随机柚取七、八、九年级男生各40人的成绩.”
根据右侧学校信息，请你简要评价小红、小明的抽样方案.
如果你来抽取120名学生的测试成绩，请给出抽样方案.
学校共有七、八、九三个年级学生近千人，各段人数相近，每段男、女生人数相当，
.....
(2)、现将随机抽取的测试成绩整理并绘制成如下统计图，请求出这组数据的平均数、中位数和众数.某校部分学生体质健康测试成绩统计图
25. 某校要从甲，乙两名学生中挑选一名学生参加数学竞赛，在最近的8次选拔赛中，他们的成绩（成绩均为整数，单位：分）如下：甲：92，95，96，88，92，98，99，100
乙：100，87，92，93，9▆，95，97，98
由于保存不当，学生乙有一次成绩的个位数字模糊不清，
(1)、求甲成绩的平均数和中位数；(2)、求事件“甲成绩的平均数大于乙成绩的平均数”的概率；(3)、当甲成绩的平均数与乙成绩的平均数相等时，请用方差大小说明应选哪个学生参加数学竞赛．26. 某中学九年级学生共进行了五次体育模拟测试，已知甲、乙两位同学五次模拟测试成绩的总分相同，小明根据甲同学的五次测试成绩绘制了尚不完整的统计表，并给出了乙同学五次测试成绩的方差的计算过程.甲同学五次体育模拟测试成绩统计表
次数
第一次
第二次
第三次
第四次
第五次
成绩（分）
35
39
37
40
小明将乙同学五次模拟测试成绩直接代入方差公式，计算过程如下：
根据上述信息，完成下列问题：
(1)、a的值是；(2)、根据甲、乙两位同学这五次模拟测试成绩，你认为谁的体育成绩更好？并说明理由；(3)、如果甲再测试1次，第六次模拟测试成绩为38分，与前5次相比，甲6次模拟测试成绩的方差.（填“变大”“变小”或“不变”）27. 为了从小华和小亮两人中选拔一人参加射击比赛，现对他们的射击水平进行测试，两人在相同条件下各射击6次，命中的环数如下（单位：环）：小华：7，8，7，8，9，9； 小亮：5，8，7，8，10，10.
(1)、填写下表：平均数（环）
中位数（环）
方差（环2）
小华
8
小亮
8
3
(2)、根据以上信息，你认为教练会选择谁参加比赛，理由是什么？(3)、若小亮再射击2次，分别命中7环和9环，则小亮这8次射击成绩的方差.（填“变大”、“变小”、“不变”）28. 某公司销售部有营业员15人，该公司为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励，为了确定一个适当的月销售目标，公司有关部门统计了这15人某月的销售量，如下表所示：月销售量/件数
1770
480
220
180
120
90
人数
1
1
3
3
3
4
(1)、直接写出这15名营业员该月销售量数据的平均数、中位数、众数；(2)、如果想让一半左右的营业员都能达到月销售目标，你认为（1）中的平均数、中位数、众数中，哪个最适合作为月销售目标？请说明理由．温馨提示：确定一个适当的月销售目标是一个关键问题；如果目标定得太高，多数营业员完不成任务，会使营业员失去信心；如果目标定得太低，不能发挥营业员的潜力．