备考2022年中考数学一轮复习（湘教版）专题68 统计的简单应用
试卷更新日期：2021-09-23 类型：一轮复习
一、单选题
-
1. 15名学生演讲赛的成绩各不相同，若某选手想知道自己能否进入前8名，则他不仅要知道自己的成绩（ ）A、 平均数 B、众数 C、方差 D、中位数2. 某校为了解学生的睡眠情况，随机调查部分学生一周平均每天的睡时间，统计结果如表：
时间/小时
7
8
9
10
人数
6
9
11
4
这些学生睡眠时间的众数、中位数是（ ）
A、众数是11，中位数是8.5 B、众数是9，中位数是8.5 C、众数是9，中位数是9 D、众数是10，中位数是93. 近些年来，移动支付已成为人们的主要支付方式之一．某企业为了解员工某月 两种移动支付方式的使用情况，从企业2000名员工中随机抽取了200人，发现样本中 两种支付方式都不使用的有10人，样本中仅使用 种支付方式和仅使用 种支付方式的员工支付金额 （元）分布情况如下表：支付金额 （元）
仅使用
36人
18人
6人
仅使用
20人
28人
2人
下面有四个推断：
①根据样本数据估计，企业2000名员工中，同时使用 两种支付方式的为800人；②本次调查抽取的样本容量为200人；③样本中仅使用 种支付方式的员工，该月支付金额的中位数一定不超过1000元；④样本中仅使用 种支付方式的员工，该月支付金额的众数一定为1500元．其中正确的是（ ）
A、①③ B、③④ C、①② D、②④4. 甲、乙、丙、丁四人10次随堂测验的成绩如图所示，从图中可以看出这10次测验平均成绩较高且较稳定的是（ ）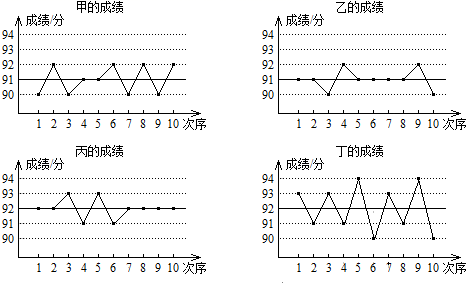
A、甲 B、乙 C、丙 D、丁5. 某班50名学生一周阅读课外书籍时间如下表所示：时间/h
6
7
8
9
人数
7
18
15
10
那么该班50名学生一周阅读课外书籍时间的众数、中位数分别是（ ）
A、18，16.5 B、18，7.5 C、7，8 D、7，7.56. 某班40名同学一周参加体育锻炼时间统计如表所示：时间/h
6
7
8
9
人数
2
18
14
6
那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是（ ）
A、18，7.5 B、18，7 C、7，8 D、7，7.57. 甲、乙两人进行飞镖比赛，每人各投6次，他们的成绩如下表（单位：环）：甲
6，7，8，8，9，9
乙
5，6，x，9，9，10
如果两人的比赛成绩的中位数相同，那么乙的第三次成绩x是（ ）
A、6环 B、7环 C、8环 D、9环8. 全民反诈，刻不容缓！陈科同学参加学校举行的“防诈骗”主题演讲比赛，五位评委给出的分数分别为90，80，86，90，94，则这组数据的中位数和众数分别是（ ）A、80，90 B、90，90 C、86，90 D、90，949. 为了向建党一百周年献礼，我市中小学生开展了红色经典故事演讲比赛.某参赛小组6名同学的成绩（单位：分）分别为：85，82，86，82，83，92.关于这组数据，下列说法错误的是（ ）A、众数是82 B、中位数是84 C、方差是84 D、平均数是8510. 小明收集了鄂尔多斯市某酒店2021年3月1日～3月6日每天的用水量（单位：吨），整理并绘制成如图所示的折线统计图，下列结论正确的是（ ）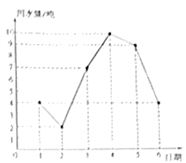
A、平均数是 B、众数是10 C、中位数是8.5 D、方差是二、填空题
-
11. 甲乙两班举行一分钟跳绳比赛，参赛学生每分钟跳绳次数的统计结果如表：
班级
参加人数
中位数
方差
平均数
甲
45
109
181
110
乙
45
111
108
110
某同学分析如表后得到如下结论：①甲，乙两班学生平均成绩相同；②乙班优秀人数多于甲班优秀人数（每分钟跳绳≥110次为优秀）；③甲班成绩的波动比乙班大，则正确结论的序号是 ．
12. 在某次体育测试中，甲、乙两班成绩的平均数、中位数、方差如下表所示，规定学生个人成绩大于90分为优秀，则甲、乙两班中优秀人数更多的是班.人数
平均数
中位数
方差
甲班
45
82
91
19.3
乙班
45
87
89
5.8
13. 东方红学校举行“学党史，听党话，跟党走”讲故事比赛，七位评委对其中一位选手的评分分别为：85，87，89，91，85，92，90.则这组数据的中位数为.14. 2020年我国是全球主要经济体中唯一实现经济正增长的国家，各行各业蓬勃发展，其中快递业务保持着较快的增长．给出了快递业务的有关数据信息．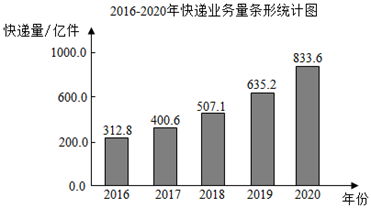
2016﹣2017年快递业务量增长速度统计表
年龄
2016
2017
2018
2019
2020
增长速度
51.4%
28.0%
26.6%
25.3%
31.2%
说明：增长速度计算办法为：增长速度=（本年业务量-去年业务量）÷去年业务量×100%．
根据图中信息，解答下列问题：
(1)、2016﹣2020年快递业务量最多年份的业务量是亿件．(2)、2016﹣2020年快递业务量增长速度的中位数是 ．(3)、下列推断合理的是（填序号）．①因为2016﹣2019年快递业务量的增长速度逐年下降，所以预估2021年的快递业务量应低于2020年的快递业务量；
②因为2016﹣2020年快递业务量每年的增长速度均在25%以上．所以预估2021年快递业务量应在 亿件以上．
15. 临近中考，报考体育专项的同学利用课余时间紧张地训练，甲、乙两名同学最近20次立定跳远成绩的平均值都是 ，方差分别是： ，这两名同学成绩比较稳定的是（填“甲”或“乙”）.16. 永州市教育部门为了了解全市中小学安全教育情况，对某校进行了“防溺水”安全知识的测试．从七年级随机抽取了50名学生的测试成绩（百分制），整理样本数据，得到下表：成绩 90≤x≤100 80≤x<90 70≤x<80 60≤x<70 x<60 人数 25 15 5 4 1 根据抽样调查结果，估计该校七年级600名学生中，80分（含80分）以上的学生有人．
17. 为了解某区六年级8400名学生中会游泳的学生人数，随机调查了其中400名学生，结果有150名学生会游泳，那么估计该区会游泳的六年级学生人数约为 ．18. 长沙地铁3号线、5号线即将运行，为了解市民每周乘地铁出行的次数，某校园小记者随机调查了100名市民，得到了如下的统计表：次数 7次及以上 6 5 4 3 2 1次及一下 人数 8 12 31 24 15 6 4 这次调查的众数和中位数分别是 ．
19. 质检部门从 件电子元件中随机抽取 件进行检测，其中有 件是次品．试据此估计这批电子元件中大约有件次品．20. 祖冲之是中国数学史上第一个名列正史的数学家，他把圆周率精确到小数点后7位，这是祖冲之最重要的数学贡献，胡老师对圆周率的小数点后100位数字进行了如下统计：数字
0
1
2
3
4
5
6
7
8
9
频数
8
8
12
11
10
8
9
8
12
14
那么，圆周率的小数点后100位数字的众数为 ．
三、作图题
-
21. “低碳生活，绿色出行”是我们倡导的一种生活方式，某校为了解学生对共享单车的使用情况，随机抽取部分学生进行问卷调查，并将这次调查的结果绘制了以下两幅不完整的统计图。
根据所给信息，解答下列问题：
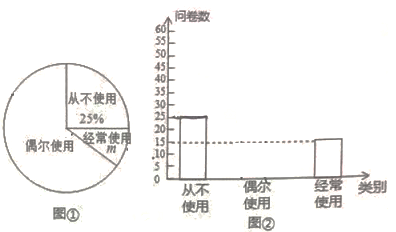(1)、m=15%；(2)、补全条形统计图；(3)、这次调查结果的众数是；(4)、已知全校共3000名学生，请估计“经常使用”共享单车的学生大约有多少名？22. 为了解学生对70周年国庆阅兵仪式直播的收看情况，某校对部分学生进行了一次调査，调査直播收看情况分三种：A．全程收看直播；B．观看了一部分直播；C．没有观看.学校学生会将调査数据进行了整理，并绘制了如下两幅不完整的统计图，请根据相关信息，解答下列问题：
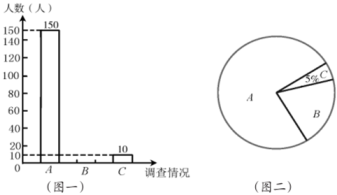(1)、本次活动共调查了名学生；(2)、图二中 区域的圆心角的度数为；(3)、补全图；(4)、若该校学生共有3000名，请估计该校学生全程收看直播的人数是多少？23. 为了解中考体育科目训练情况，某区从全区九年级学生中随机抽取了部分学生进行了一次中考体育科目测试（把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格），并将测试结果绘成了如下两幅不完整的统计图。请根据统计图中的信息解答下列问题：
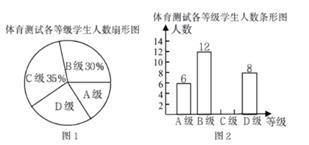(1)、求本次抽样测试的学生人数是多少？(2)、通过计算将条形统计图补充完整；(3)、该区九年级有学生6000名，如果全部参加这次中考体育科目测试，请估计优秀的人约有多少人？24. 受非洲猪瘟疫情影响，2019年我国猪肉价格有较大幅度的上升.为了解某地区养殖户的受灾情况，现从该地区建档的养殖户中随机抽取了部分养殖户进行调查（把调查结果分为四个等级：A级—非常严重，B级—严重，C级—般，D级—没有感染），并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解答下列问题：所抽取养殖户受灾情况统计图
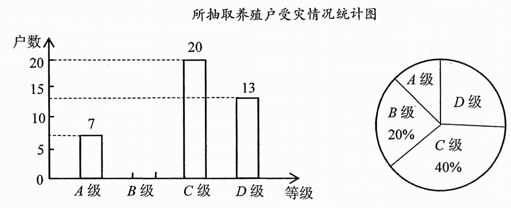(1)、填空：本次抽样调查的养殖户的总户数是 ， 在扇形统计图中A级所对应的圆心角为.(2)、请补全条形统计图；(3)、若该地区建档的养殖户有1500户，估计非常严重与严重的养殖户一共有多少户?四、解答题
-
25. 一般来说，要了解一个城市的空气污染情况，观察一个月得到的结论可靠，还是春、夏、秋、冬各观察一个月得到的结论可靠？26. 海静中学开展以“我最喜爱的职业”为主题的调查活动，围绕“在演员、教师、医生、律师、公务员共五类职业中，你最喜爱哪一类？（必选且只选一类）”的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的统计图，请你根据图中提供的信息回答下列问题：
(1)、本次调查共抽取了多少名学生？(2)、求在被调查的学生中，最喜爱教师职业的人数，并补全条形统计图；(3)、若海静中学共有1500名学生，请你估计该中学最喜爱律师职业的学生有多少名？27. 某市一家园林公司培育出新品种树苗，为考察这种树苗的移植的成活率，公司进行了统计，结果如图所示．累积移植总数（棵）
100
500
1000
2000
5000
10000
成活率
0.910
0.968
0.942
0.956
0.947
0.950
现该市实施绿化工程，需移植一批这种树苗，若这批树苗移植后要有28.5万棵成活，则需要一次性移植多少棵树苗较为合适？请说明理由．
28. 某校文学社为了解学生课外阅读情况，抽样调查了部分学生每周用于课外阅读的时间，过程如下：数据收集：从全校随机抽取20名学生，进行了每周用于课外阅读时间的调查，数据如下（单位：min）：
30
60
81
50
40
110
130
146
90
100
60
81
120
140
70
81
10
20
100
81
整理数据：按如下分段整理样本数据并补全表格：
课外阅读时间x（min）
0≤x<40
40≤x<80
80≤x<120
120≤x<160
等级
D
C
B
A
人数
3
▲
8
▲
分析数据：补全下列表格中的统计量：
平均数
中位数
众数
80
▲
▲
得出结论：
⑴用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为 ▲ ；
⑵如果该校现有学生400人，估计等级为“B”的学生有多少人？
⑶假设平均阅读一本课外书的时间为320分钟，请你选择样本中的一种统计量估计该校学生每人一年（按52周计算）平均阅读多少本课外书?
五、综合题
-
29. 某校计划举办以“庆祝建党百年，传承红色基因”为主题的系列活动，活氛围红歌演唱、诗歌朗诵、爱国征文及党史知识竞赛，要求每名学生都参加活动且只能选择一项活动为了解学生参加活动的情况，随机选取该学校部分学生进行调查，以下是根据调查结果绘制的统计图表的一部分．
活动项目
频数（人）
频率
红歌演唱
10
0.2
诗歌朗诵
爱国征文
党史知识竞赛
0.1
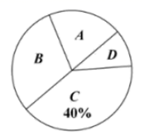
据以上信息，回答下列问题：
(1)、被调查的学生中，参加红歌演唱活动的学生人数为人，参加爱国征文活动的学生人数占被调查学生总人数的百分比为%；(2)、本次调查的样本容量为 ， 样本中参加党史知识竞赛活动的学生人数为人；(3)、若该校共有800名学生，请根据调查结果，估计参加诗歌朗诵活动的学生人数．30. 某中学为了解初三学生参加志愿者活动的次数，随机调查了该年级20名学生，统计得到该20名学生参加志愿者活动的次数如下：3；5；3；6；3；4；4；5；2；4；5；6；1；3；5；5；4；4；2；4根据以上数据，得到如下不完整的频数分布表：
次数
1
2
3
4
5
6
人数
1
2
a
6
b
2
(1)、表格中的 ， ；(2)、在这次调查中，参加志愿者活动的次数的众数为 ， 中位数为；(3)、若该校初三年级共有300名学生，根据调查统计结果，估计该校初三年级学生参加志愿者活动的次数为4次的人数．31. 某中学九年级举办中华优秀传统文化知识竞赛．用简单随机抽样的方法，从该年级全体600名学生中抽取20名，其竞赛成绩如图：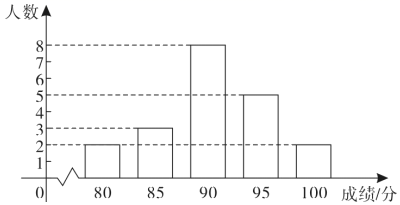
(1)、求这20名学生成绩的众数，中位数和平均数；(2)、若规定成绩大于或等于90分为优秀等级，试估计该年级获优秀等级的学生人数．32. 垃圾的分类回收不仅能够减少环境污染，美化家园，甚至能够变废为宝，节约能源，为增强学生垃圾分类意识，推动垃圾分类进校园，某中学组织全校1565名学生参加了“垃圾分类知识竞赛”（满分为100分），该校数学兴趣小组为了解全校学生竞赛分数情况，采用简单随机抽样的方法（即每名学生的竞赛分数被抽到的可能性相等的抽样方法）抽取部分学生的竞赛分数进行调查分析．(1)、以下三种抽样调查方案：方案一：从七年级、八年级、九年级中指定部分学生的竞赛分数作为样本；
方案二：从七年级、八年级中随机抽取部分男生的竞赛分数以及在九年级中随机抽取部分女生的竞赛分数作为样本；
方案三：从全校1565名学生的竞赛分数中随机抽取部分学生的竞赛分数作为样本，其中抽取的样最具有代表性和广泛性的一种抽样调查方案是（填写“方案一”、“方案二”或“方案三”）；
(2)、该校数学兴趣小组根据简单随机抽样方法获得的样本，绘制出如下统计表（90分及以上为“优秀”，60分及以上为“及格”，学生竞赛分数记为x分）样本容量
平均分
及格率
优秀率
最高分
最低分
100
83.59
95%
40%
100
52
分数段
频数
5
7
18
30
40
结合上述信息解答下列问题：
①样本数据的中位数所在分数段为；
②全校1565名学生，估计竞赛分数达到“优秀”的学生有人．