备考2022年中考数学一轮复习(湘教版)专题63 直棱柱、 圆锥的侧面展开图
试卷更新日期:2021-09-23 类型:一轮复习
一、单选题
-
1. 将正方体的表面沿某些棱剪开,展成如图所示的平面图形,则原正方体中与数字5所在的面相对的面上标的数字为( )
 A、1 B、2 C、3 D、42. 下列四个图形中,不能作为正方体的展开图的是( )A、
A、1 B、2 C、3 D、42. 下列四个图形中,不能作为正方体的展开图的是( )A、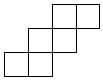 B、
B、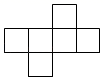 C、
C、 D、
D、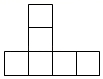 3. 用一个半径为 面积为 的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为( )A、 B、 C、2 D、14. 如图,正方形 的边长为4,以点A为圆心, 为半径画圆弧 得到扇形 (阴影部分,点E在对角线 上).若扇形 正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
3. 用一个半径为 面积为 的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为( )A、 B、 C、2 D、14. 如图,正方形 的边长为4,以点A为圆心, 为半径画圆弧 得到扇形 (阴影部分,点E在对角线 上).若扇形 正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( ) A、 B、1 C、 D、5. 下列正方体的展开图上每个面上都有一个汉字.其中,手的对面是口的是( )A、
A、 B、1 C、 D、5. 下列正方体的展开图上每个面上都有一个汉字.其中,手的对面是口的是( )A、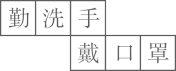 B、
B、 C、
C、 D、
D、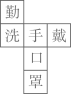 6. 如图所示,正方体的展开图为( )
6. 如图所示,正方体的展开图为( ) A、
A、 B、
B、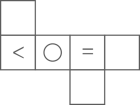 C、
C、 D、
D、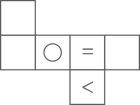
二、填空题
-
7. 用半径为50,圆心角为120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面半径为.8. 底面半径为3,母线长为4的圆锥的侧面积为.(结果保留 )9. 如图是某圆柱体果罐,它的主视图是边长为 的正方形,该果罐侧面积为 .
 10. 如图,小梅把一顶底面半径为 的圆锥形小丑纸帽沿一条母线剪开并展平,得到一个圆心角为 的扇形纸片,那么扇形纸片的半径为 .
10. 如图,小梅把一顶底面半径为 的圆锥形小丑纸帽沿一条母线剪开并展平,得到一个圆心角为 的扇形纸片,那么扇形纸片的半径为 . 11. 已知圆锥的母线长为10,高为8,则该圆锥的侧面展开图(扇形)的弧长为 . (用含π的代数式表示),圆心角为度.12. 一个圆柱形橡皮泥,底面积是 .高是 .如果用这个橡皮泥的一半,把它捏成高为 的圆锥,则这个圆锥的底面积是
11. 已知圆锥的母线长为10,高为8,则该圆锥的侧面展开图(扇形)的弧长为 . (用含π的代数式表示),圆心角为度.12. 一个圆柱形橡皮泥,底面积是 .高是 .如果用这个橡皮泥的一半,把它捏成高为 的圆锥,则这个圆锥的底面积是三、作图题
-
13.
如图是一张长方形硬纸片,正好分成15个完全相同的小正方形,现要把它们剪切成3份,使每份有5个小正方形相连,折起来都可以围成一个没有盖的正方体纸盒.请在图中用实线画出一种剪切线.
 14. 将立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平,可以得到其表面展开图的平面图形.(1)、以下两个方格图中的阴影部分能表示立方体表面展开图的是(填A或B).
14. 将立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平,可以得到其表面展开图的平面图形.(1)、以下两个方格图中的阴影部分能表示立方体表面展开图的是(填A或B).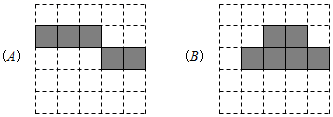 (2)、在以下方格图中,画一个与(1)中呈现的阴影部分不相似(包括不全等)的立方体表面展开图.(用阴影表示)
(2)、在以下方格图中,画一个与(1)中呈现的阴影部分不相似(包括不全等)的立方体表面展开图.(用阴影表示) (3)、如图中的实线是立方体纸盒的剪裁线,请将其表面展开图画在右图的方格图中.(用阴影表示)
(3)、如图中的实线是立方体纸盒的剪裁线,请将其表面展开图画在右图的方格图中.(用阴影表示)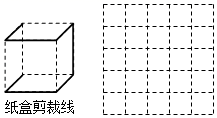
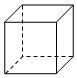 15. 一个等腰Rt△ABC如图所示,将它绕着直线AC旋转一周,形成一个几何体.
15. 一个等腰Rt△ABC如图所示,将它绕着直线AC旋转一周,形成一个几何体. (1)、画出这个几何体的三视图.(2)、依据图中的测量数据,计算这个几何体的表面积.16. 画一个正方体的三种平面展开图,要求展开图是中心对称图形.
(1)、画出这个几何体的三视图.(2)、依据图中的测量数据,计算这个几何体的表面积.16. 画一个正方体的三种平面展开图,要求展开图是中心对称图形.
四、解答题
-
17. 如图所示,在 Rt△ABC中,∠C=90°,AC=4 ,BC=3 .求以直角边所在直线为轴,把△ABC 旋转一周得到的圆锥的侧面积.
 18. 如图①是山东舰徽的构图,采用航母 度破浪而出的角度,展现山东舰作为中国首艘国产舰母横空出世的气势,将舰徽中第一条波浪抽象成几何图形,则是一条长为 的弧,若该弧所在的扇形是高为 的圆锥侧面展开图(如图②),则该圆锥的母线长 为多少?
18. 如图①是山东舰徽的构图,采用航母 度破浪而出的角度,展现山东舰作为中国首艘国产舰母横空出世的气势,将舰徽中第一条波浪抽象成几何图形,则是一条长为 的弧,若该弧所在的扇形是高为 的圆锥侧面展开图(如图②),则该圆锥的母线长 为多少? 19. 如图, 为正方形, ,以点 为圆心, 为半径画弧得到扇形 ,现将该扇形围成一圆锥的侧面,求该圆锥底面圆的半径.
19. 如图, 为正方形, ,以点 为圆心, 为半径画弧得到扇形 ,现将该扇形围成一圆锥的侧面,求该圆锥底面圆的半径. 20. 如图从一块半径为 的圆形铁皮上剪出一个圆心角为 的扇形,再把此扇形围成一个圆锥,求圆锥的底面半径.
20. 如图从一块半径为 的圆形铁皮上剪出一个圆心角为 的扇形,再把此扇形围成一个圆锥,求圆锥的底面半径.
五、综合题
-
21. 如图①,已知圆锥的母线长l=16cm,若以顶点O为中心,将此圆锥按图②放置在平面上逆时针滚动3圈后所形成的扇形的圆心角θ=270°.
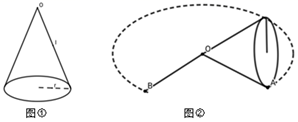 (1)、求圆锥的底面半径;(2)、求圆锥的表面积.
(1)、求圆锥的底面半径;(2)、求圆锥的表面积.

