备考2022年中考数学一轮复习(湘教版)专题61 解直角三角形及其应用
试卷更新日期:2021-09-23 类型:一轮复习
一、单选题
-
1. 如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据: ≈1.732)( )
 A、136.6米 B、86.7米 C、186.7米 D、86.6米2. 如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为( )米
A、136.6米 B、86.7米 C、186.7米 D、86.6米2. 如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为( )米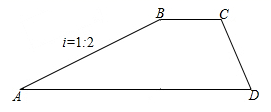 A、 B、 C、 D、243. 如图,D为Rt ABC的AC边上一点,∠DBC=∠A,AC=4,cosA= ,则BD=( )
A、 B、 C、 D、243. 如图,D为Rt ABC的AC边上一点,∠DBC=∠A,AC=4,cosA= ,则BD=( ) A、 B、 C、 D、44. 保利观澜旁边有一望江公园,公园里有一文峰塔,工程人员在与塔底中心的 同一水平线的 处,测得 米,沿坡度 的斜坡 走到 点,测得塔顶 仰角为37°,再沿水平方向走20米到 处,测得塔顶 的仰角为22°,则塔高 为( )米.(结果精确到十分位)( , , , , , )
A、 B、 C、 D、44. 保利观澜旁边有一望江公园,公园里有一文峰塔,工程人员在与塔底中心的 同一水平线的 处,测得 米,沿坡度 的斜坡 走到 点,测得塔顶 仰角为37°,再沿水平方向走20米到 处,测得塔顶 的仰角为22°,则塔高 为( )米.(结果精确到十分位)( , , , , , ) A、18.3米 B、19.3米 C、20米 D、21.2米5. 如图,我市在建的鄂咸高速太和新城段路基的横断面为梯形ABCD,DC∥AB,斜坡AD长为8米,坡角α为30°,斜坡BC的坡角β为45°,则斜坡BC的长为( )
A、18.3米 B、19.3米 C、20米 D、21.2米5. 如图,我市在建的鄂咸高速太和新城段路基的横断面为梯形ABCD,DC∥AB,斜坡AD长为8米,坡角α为30°,斜坡BC的坡角β为45°,则斜坡BC的长为( ) A、6米 B、 米 C、4米 D、 米6. 如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为 ,则这栋楼的高度为( )
A、6米 B、 米 C、4米 D、 米6. 如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为 ,则这栋楼的高度为( )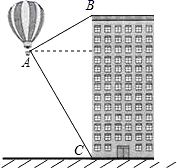 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 如图,海中有一个小岛 ,一艘轮船由西向东航行,在 点测得小岛 在北偏东 方向上;航行 到达 点,这时测得小岛 在北偏东 方向上.小岛 到航线 的距离是 ( ,结果用四舍五入法精确到0.1).
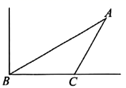 8. 如图,建筑物 上有一高为 的旗杆 ,从D处观测旗杆顶部A的仰角为 ,观测旗杆底部B的仰角为 ,则建筑物 的高约为 (结果保留小数点后一位).(参考数据 , , )
8. 如图,建筑物 上有一高为 的旗杆 ,从D处观测旗杆顶部A的仰角为 ,观测旗杆底部B的仰角为 ,则建筑物 的高约为 (结果保留小数点后一位).(参考数据 , , ) 9. 某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头C测一段水平雪道一端A处的俯角为50°,另一端B处的俯角为45°,若无人机镜头 处的高度 为 米,点A , D , B在同一直线上,则通道AB的长度为米.(结果保留整数,参考数据 , , )
9. 某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头C测一段水平雪道一端A处的俯角为50°,另一端B处的俯角为45°,若无人机镜头 处的高度 为 米,点A , D , B在同一直线上,则通道AB的长度为米.(结果保留整数,参考数据 , , )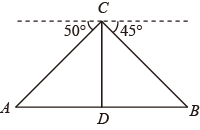 10. 如图,为了测量“四川大渡河峡谷”石碑的高度,佳佳在点C处测得石碑顶A点的仰角为 ,她朝石碑前行5米到达点D处,又测得石顶A点的仰角为 ,那么石碑的高度 的长 米.(结果保留根号)
10. 如图,为了测量“四川大渡河峡谷”石碑的高度,佳佳在点C处测得石碑顶A点的仰角为 ,她朝石碑前行5米到达点D处,又测得石顶A点的仰角为 ,那么石碑的高度 的长 米.(结果保留根号) 11. 太原地铁2号线是山西省第一条开通运营的地铁线路,于2020年12月26日开通.如图是该地铁某站扶梯的示意图,扶梯 的坡度 ( 为铅直高度与水平宽度的比).王老师乘扶梯从扶梯底端 以0.5米/秒的速度用时40秒到达扶梯顶端 ,则王老师上升的铅直高度 为米.
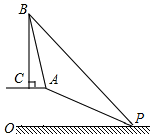
11. 太原地铁2号线是山西省第一条开通运营的地铁线路,于2020年12月26日开通.如图是该地铁某站扶梯的示意图,扶梯 的坡度 ( 为铅直高度与水平宽度的比).王老师乘扶梯从扶梯底端 以0.5米/秒的速度用时40秒到达扶梯顶端 ,则王老师上升的铅直高度 为米. 12. 如图,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为71.6°,且AC平行与地面OP,则古塔BC的高度为米(精确到1米).
12. 如图,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为71.6°,且AC平行与地面OP,则古塔BC的高度为米(精确到1米).(参考数据:sin71.6°≈0.95,cos71.6°≈0.316,tan71.6°≈3)
三、解答题
-
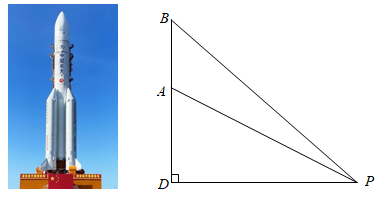
13. 我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角 为 且A与P两点的距离为6千米,它沿铅垂线上升75秒后到达B处,此时在P处测得B点的仰角 为 ,求天舟二号从A处到B处的平均速度.(结果精确到 ,取 )
 14. 开凿于北魏孝文帝年间的龙门石窟是中国石刻艺术瑰宝,卢舍那佛像是石窟中最大的佛像.某数学活动小组到龙门石窟景区测量这尊佛像的高度.如图,他们选取的测量点 与佛像 的底部 在同一水平线上.已知佛像头部 为 ,在 处测得佛像头顶部 的仰角为 ,头底部 的仰角为 ,求佛像 的高度(结果精确到 .参考数据: , , )
14. 开凿于北魏孝文帝年间的龙门石窟是中国石刻艺术瑰宝,卢舍那佛像是石窟中最大的佛像.某数学活动小组到龙门石窟景区测量这尊佛像的高度.如图,他们选取的测量点 与佛像 的底部 在同一水平线上.已知佛像头部 为 ,在 处测得佛像头顶部 的仰角为 ,头底部 的仰角为 ,求佛像 的高度(结果精确到 .参考数据: , , ) 15. 如图,为了测量某建筑物CD的高度,在地面上取A,B两点,使A、B、D三点在同一条直线上,拉姆同学在点A处测得该建筑物顶部C的仰角为30°,小明同学在点B处测得该建筑物顶部C的仰角为45°,且AB=10m.求建筑物CD的高度.(拉姆和小明同学的身高忽略不计.结果精确到0.1m, ≈1.732)
15. 如图,为了测量某建筑物CD的高度,在地面上取A,B两点,使A、B、D三点在同一条直线上,拉姆同学在点A处测得该建筑物顶部C的仰角为30°,小明同学在点B处测得该建筑物顶部C的仰角为45°,且AB=10m.求建筑物CD的高度.(拉姆和小明同学的身高忽略不计.结果精确到0.1m, ≈1.732)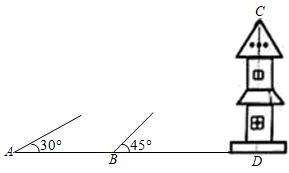 16. 如图,一艘轮船离开 港沿着东北方向直线航行 海里到达 处,然后改变航向,向正东方向航行20海里到达 处,求 的距离.
16. 如图,一艘轮船离开 港沿着东北方向直线航行 海里到达 处,然后改变航向,向正东方向航行20海里到达 处,求 的距离.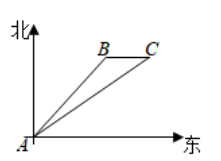 17. 如图,在一座山的前方有一栋住宅,已知山高 m,楼高 m,某天上午9时太阳光线从山顶点 处照射到住宅的点 外.在点 处测得点 的俯角 ,上午10时太阳光线从山顶点 处照射到住宅点 处,在点 处测得点 的俯角 ,已知每层楼的高度为3m, m,问:以当天测量数据为依据,不考虑季节天气变化,至少要买该住宅的第几层楼,才能使上午10时太阳光线照射到该层楼的外墙?( )
17. 如图,在一座山的前方有一栋住宅,已知山高 m,楼高 m,某天上午9时太阳光线从山顶点 处照射到住宅的点 外.在点 处测得点 的俯角 ,上午10时太阳光线从山顶点 处照射到住宅点 处,在点 处测得点 的俯角 ,已知每层楼的高度为3m, m,问:以当天测量数据为依据,不考虑季节天气变化,至少要买该住宅的第几层楼,才能使上午10时太阳光线照射到该层楼的外墙?( )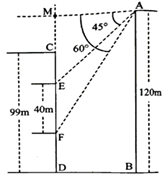 18. 在一次测量物体高度的数学实践活动中,小明从一条笔直公路上选择三盏高度相同的路灯进行测量.如图,他先在点B处安置测倾器,于点A处测得路灯MN顶端的仰角为 ,再沿BN方向前进10米,到达点D处,于点C处测得路灯PQ顶端的仰角为 .若测倾器的高度为1.2米,每相邻两根灯柱之间的距离相等,求路灯的高度(结果精确到0.1米).
18. 在一次测量物体高度的数学实践活动中,小明从一条笔直公路上选择三盏高度相同的路灯进行测量.如图,他先在点B处安置测倾器,于点A处测得路灯MN顶端的仰角为 ,再沿BN方向前进10米,到达点D处,于点C处测得路灯PQ顶端的仰角为 .若测倾器的高度为1.2米,每相邻两根灯柱之间的距离相等,求路灯的高度(结果精确到0.1米).(参考数据: , , , , , )

四、综合题
-
19. 如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到一定高度D点处时,无人机测得操控者A的俯角为 ,测得小区楼房 顶端点C处的俯角为 .已知操控者A和小区楼房 之间的距离为45米,小区楼房 的高度为 米.
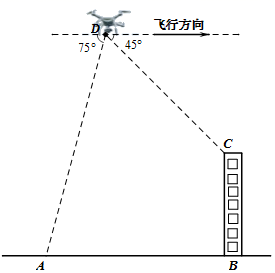 (1)、求此时无人机的高度;(2)、在(1)条件下,若无人机保持现有高度沿平行于 的方向,并以5米/秒的速度继续向前匀速飞行.问:经过多少秒时,无人机刚好离开了操控者的视线?(假定点A,B,C,D都在同一平面内.参考数据: , .计算结果保留根号)20. 在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东 方向有一信号发射塔P.他由A地沿正东方向骑行 km到达B地,此时发现信号塔P在他的北偏东 方向,然后他由B地沿北偏东 方向骑行12km到达C地.
(1)、求此时无人机的高度;(2)、在(1)条件下,若无人机保持现有高度沿平行于 的方向,并以5米/秒的速度继续向前匀速飞行.问:经过多少秒时,无人机刚好离开了操控者的视线?(假定点A,B,C,D都在同一平面内.参考数据: , .计算结果保留根号)20. 在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东 方向有一信号发射塔P.他由A地沿正东方向骑行 km到达B地,此时发现信号塔P在他的北偏东 方向,然后他由B地沿北偏东 方向骑行12km到达C地.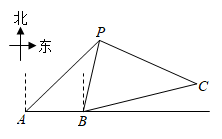 (1)、求A地与信号发射塔P之间的距离;(2)、求C地与信号发射塔P之间的距离.(计算结果保留根号)21. 某镇为创建特色小镇,助力乡村振兴,决定在辖区的一条河上修建一座步行观光桥,如图,该河旁有一座小山,山高 ,坡面 的坡度 (注:从山顶 处测得河岸 和对岸 的俯角分别为 , .
(1)、求A地与信号发射塔P之间的距离;(2)、求C地与信号发射塔P之间的距离.(计算结果保留根号)21. 某镇为创建特色小镇,助力乡村振兴,决定在辖区的一条河上修建一座步行观光桥,如图,该河旁有一座小山,山高 ,坡面 的坡度 (注:从山顶 处测得河岸 和对岸 的俯角分别为 , .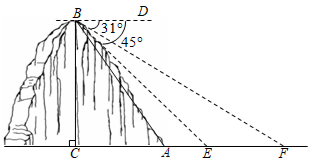
(参考数据: , , )
(1)、求山脚 到河岸 的距离;(2)、若在此处建桥,试求河宽 的长度.(结果精确到 )22. 王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,他在点C处测得大树顶端A的仰角为 ,再从C点出发沿斜坡走 米到达斜坡上D点,在点D处测得树顶端A的仰角为 ,若斜坡CF的坡比为 (点 在同一水平线上).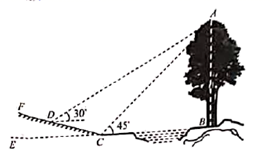 (1)、求王刚同学从点C到点D的过程中上升的高度;(2)、求大树AB的高度(结果保留根号).23. 我国纸伞的制作工艺十分巧妙.如图1,伞不管是张开还是收拢,伞柄 始终平分同一平面内两条伞骨所成的角 ,且 ,从而保证伞圈D能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图,此时伞圈D已滑动到点 的位置,且A,B, 三点共线, ,B为 中点,当 时,伞完全张开.
(1)、求王刚同学从点C到点D的过程中上升的高度;(2)、求大树AB的高度(结果保留根号).23. 我国纸伞的制作工艺十分巧妙.如图1,伞不管是张开还是收拢,伞柄 始终平分同一平面内两条伞骨所成的角 ,且 ,从而保证伞圈D能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图,此时伞圈D已滑动到点 的位置,且A,B, 三点共线, ,B为 中点,当 时,伞完全张开. (1)、求 的长.(2)、当伞从完全张开到完全收拢,求伞圈D沿着伞柄向下滑动的距离.(参考数据: )24. 我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿 摆成如图1所示.已知 ,鱼竿尾端A离岸边 ,即 .海面与地面 平行且相距 ,即 .
(1)、求 的长.(2)、当伞从完全张开到完全收拢,求伞圈D沿着伞柄向下滑动的距离.(参考数据: )24. 我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿 摆成如图1所示.已知 ,鱼竿尾端A离岸边 ,即 .海面与地面 平行且相距 ,即 .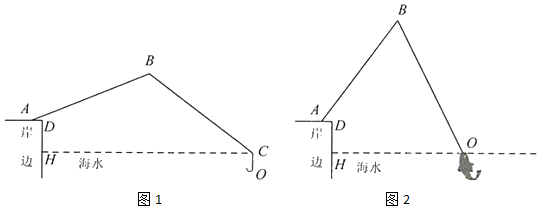 (1)、如图1,在无鱼上钩时,海面上方的鱼线 与海面 的夹角 ,海面下方的鱼线 与海面 垂直,鱼竿 与地面 的夹角 .求点O到岸边 的距离;(2)、如图2,在有鱼上钩时,鱼竿与地面的夹角 ,此时鱼线被拉直,鱼线 ,点O恰好位于海面.求点O到岸边 的距离.(参考数据: , , , , , )
(1)、如图1,在无鱼上钩时,海面上方的鱼线 与海面 的夹角 ,海面下方的鱼线 与海面 垂直,鱼竿 与地面 的夹角 .求点O到岸边 的距离;(2)、如图2,在有鱼上钩时,鱼竿与地面的夹角 ,此时鱼线被拉直,鱼线 ,点O恰好位于海面.求点O到岸边 的距离.(参考数据: , , , , , )