备考2022年中考数学一轮复习(湘教版)专题59 位似
试卷更新日期:2021-09-23 类型:一轮复习
一、单选题
-
1. 如图,在平面直角坐标系中,已知点 , , ,以某点为位似中心,作出与 的位似比为 的位似 ,则位似中心的坐标和 的值分别为( )
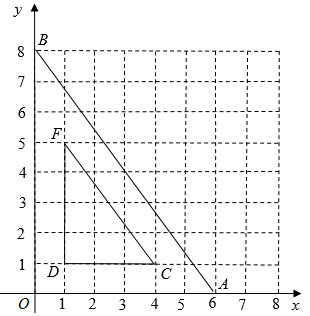 A、(0,0), B、(1,1),2 C、(2,2), D、(1,1),2. 如图, 中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作 的位似图形 ,并把 的边长放大到原来的2倍,设点B的横坐标是a , 则点B的对应点 的横坐标是( )
A、(0,0), B、(1,1),2 C、(2,2), D、(1,1),2. 如图, 中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作 的位似图形 ,并把 的边长放大到原来的2倍,设点B的横坐标是a , 则点B的对应点 的横坐标是( ) A、 B、 C、 D、3. 如图, 和 是位似三角形,位似中心为点 , ,则 和 的位似比为( )
A、 B、 C、 D、3. 如图, 和 是位似三角形,位似中心为点 , ,则 和 的位似比为( ) A、 B、 C、 D、4. 如图,图形甲与图形乙是位似图形, 是位似中心,位似比为 ,点 , 的对应点分别为点 , .若 ,则 的长为( )
A、 B、 C、 D、4. 如图,图形甲与图形乙是位似图形, 是位似中心,位似比为 ,点 , 的对应点分别为点 , .若 ,则 的长为( )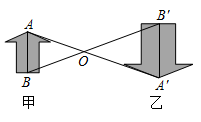 A、8 B、9 C、10 D、155. 下列各选项中的两个图形不是位似图形的是( )A、
A、8 B、9 C、10 D、155. 下列各选项中的两个图形不是位似图形的是( )A、 B、
B、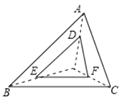 C、
C、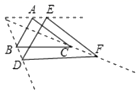 D、
D、 6. 如图,△ABC中,顶点A、B均在第二象限,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C',且△A'B'C'与△ABC的位似比为2:1,设点B的对应点B'的横坐标是3,则点B的横坐标是( )
6. 如图,△ABC中,顶点A、B均在第二象限,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C',且△A'B'C'与△ABC的位似比为2:1,设点B的对应点B'的横坐标是3,则点B的横坐标是( )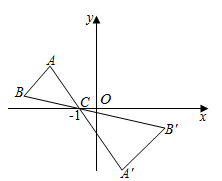 A、 B、﹣2 C、 D、﹣37. 如图,点 , ,以原点O为位似中心,把线段AB缩短为原来的一半,得到线段CD,其中点C与点A对应,点D与点B对应,则点D的横坐标为( )
A、 B、﹣2 C、 D、﹣37. 如图,点 , ,以原点O为位似中心,把线段AB缩短为原来的一半,得到线段CD,其中点C与点A对应,点D与点B对应,则点D的横坐标为( )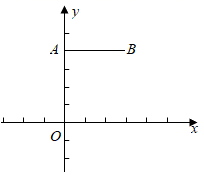 A、2 B、2或-2 C、 D、 或-8. 一个图形的各点的纵坐标乘以2,横坐标不变,这个图形发生的变化是( )A、横向拉伸为原来的2倍 B、纵向拉伸为原来的2倍 C、横向压缩为原来的 D、纵向压缩为原来的9. 平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为P′( a+1, b﹣1).已知A,B,C是不共线的三个点,它们经过这种变换后,得到的对应点分别为A′,B′,C′.若△ABC的面积为S1 , △A′B′C′的面积为S2 , 则用等式表示S1与S2的关系为( )A、S1 S2 B、S1 S2 C、S1=2S2 D、S1=4S210. 如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA′:A′A=2:1,四边形A′B′C′D′的面积为12cm2 , 则四边形 ABCD 的面积为( )
A、2 B、2或-2 C、 D、 或-8. 一个图形的各点的纵坐标乘以2,横坐标不变,这个图形发生的变化是( )A、横向拉伸为原来的2倍 B、纵向拉伸为原来的2倍 C、横向压缩为原来的 D、纵向压缩为原来的9. 平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为P′( a+1, b﹣1).已知A,B,C是不共线的三个点,它们经过这种变换后,得到的对应点分别为A′,B′,C′.若△ABC的面积为S1 , △A′B′C′的面积为S2 , 则用等式表示S1与S2的关系为( )A、S1 S2 B、S1 S2 C、S1=2S2 D、S1=4S210. 如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA′:A′A=2:1,四边形A′B′C′D′的面积为12cm2 , 则四边形 ABCD 的面积为( )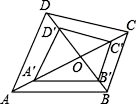 A、24cm2 B、27cm2 C、36cm2 D、54cm2
A、24cm2 B、27cm2 C、36cm2 D、54cm2二、填空题
-
11. 如图,以点 为位似中心,把 放大2倍得到 ',① ;② ;③ ;④点 、 、 三点在同一直线上.则以上四种说法正确的是 .
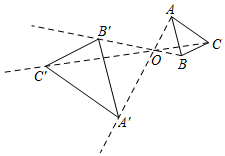 12. 如图,已知矩形OABC与矩形FEDO是位似图形,P是位似中心,若点A的坐标为(0,6),点E的坐标为(2,3),则点B的坐标为 .
12. 如图,已知矩形OABC与矩形FEDO是位似图形,P是位似中心,若点A的坐标为(0,6),点E的坐标为(2,3),则点B的坐标为 . 13. 在平面直角坐标系 中, 三个顶点的坐标分别为 , , ,以原点O为位似中心,把这个三角形缩小为原来的 得到 ,则点A的对应点C的坐标是 .14. 如图,在平面直角坐标系中, 与 是以点C为位似中心的位似图形,则其相似比为.
13. 在平面直角坐标系 中, 三个顶点的坐标分别为 , , ,以原点O为位似中心,把这个三角形缩小为原来的 得到 ,则点A的对应点C的坐标是 .14. 如图,在平面直角坐标系中, 与 是以点C为位似中心的位似图形,则其相似比为.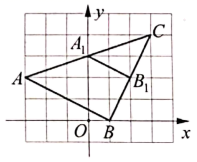 15. 如图,四边形 与四边形 位似,位似中心点是O, ,则 .
15. 如图,四边形 与四边形 位似,位似中心点是O, ,则 .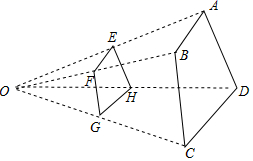 16. 在平面直角坐标系中,已知A(﹣3,3),B(﹣6,0),以原点O为位似中心,将线段AB放大为原来的2倍,得到线段 ,则 的中点坐标是 .
16. 在平面直角坐标系中,已知A(﹣3,3),B(﹣6,0),以原点O为位似中心,将线段AB放大为原来的2倍,得到线段 ,则 的中点坐标是 .三、作图题
-
17. 如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(﹣2,3),B(﹣3,2),C(﹣1,1).
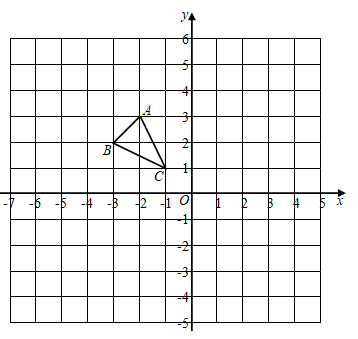 (1)、以坐标原点O为位似中心,2为位似比.将△ABC放大,得到△A´B´C´.请在平面直角坐标系中画出△A´B´C´;(2)、求出△A´B´C´的面积.18. 已知: 在平面直角坐标平面内,三个顶点的坐标分别为 、 、 (正方形网格中每个小正方形的边长是一个单位长度).
(1)、以坐标原点O为位似中心,2为位似比.将△ABC放大,得到△A´B´C´.请在平面直角坐标系中画出△A´B´C´;(2)、求出△A´B´C´的面积.18. 已知: 在平面直角坐标平面内,三个顶点的坐标分别为 、 、 (正方形网格中每个小正方形的边长是一个单位长度).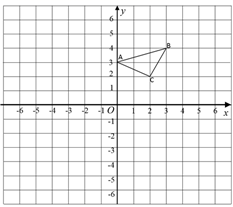
( 1 )画出 向下平移4个单位长度得到的 ,并写出点 的坐标;
( 2 )以点B为位似中心,在网格内画出 ,使 与 位似,且位似比为 ,并写出点 的坐标;
( 3 ) 的面积是多少个平方单位?
19. 如图,在平面直角坐标系中,每个小正方形的边长都是1个单位长度, 的顶点都在格点上.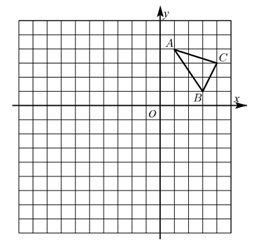 (1)、以原点O为位似中心,在第三象限内画出将 放大为原来的2倍后的位似图形 .(2)、已知 的面积为 ,则 的面积是.
(1)、以原点O为位似中心,在第三象限内画出将 放大为原来的2倍后的位似图形 .(2)、已知 的面积为 ,则 的面积是.四、解答题
-
20.
如图,已知△ABC和△A′B′C′是位似比为2的位似三角形,且AB的对应边是A′B′,请用尺规作图,将△A′B′C′补充完整(可不写作法,但保留作图痕迹).
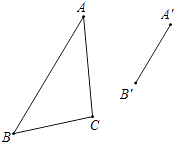 21. 如图,以原点O为位似中心,把△OAB放大后得到△OCD,求△OAB与△OCD的相似比.
21. 如图,以原点O为位似中心,把△OAB放大后得到△OCD,求△OAB与△OCD的相似比. 22.
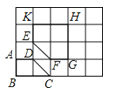
22.如图,在4×5网格图中,其中每个小正方形边长均为1,梯形ABCD和五边形EFGHK的顶点均为小正方形的顶点.
(1)以B为位似中心,在网格图中作四边形A′BC′D′,使四边形A′BC′D′和梯形ABCD位似,且位似比为2:1;
(2)求(1)中四边形A′BC′D′与五边形EFGHK重叠部分的周长.(结果保留根号)
 23.
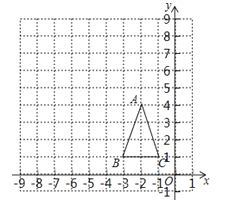
23.如图,△ABC的三个顶点坐标分别为A(﹣2,4)、B(﹣3,1)、C(﹣1,1),以坐标原点O为位似中心,相似比为2,在第二象限内将△ABC放大,放大后得到△A′B′C′.
(1)画出放大后的△A′B′C′,并写出点A′、B′、C′的坐标.(点A、B、C的对应点为A′、B′、C′)
(2)求△A′B′C′的面积.
五、综合题
-
24. 如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.
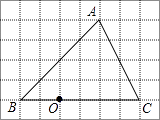 (1)、在图中△ABC的内部作△A′B′C′,使△A′B′C′和△ABC位似,且位似中心为点O,位似比为1:2;(2)、连接(1)中的AA′,则线段AA′的长度是 .25. 如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3 .
(1)、在图中△ABC的内部作△A′B′C′,使△A′B′C′和△ABC位似,且位似中心为点O,位似比为1:2;(2)、连接(1)中的AA′,则线段AA′的长度是 .25. 如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3 .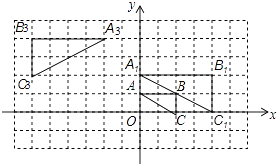 (1)、△ABC与△A1B1C1的位似比等于;(2)、在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;(3)、请写出△A3B3C3是由△A2B2C2怎样平移得到的?(4)、设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .26. 如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)、△ABC与△A1B1C1的位似比等于;(2)、在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;(3)、请写出△A3B3C3是由△A2B2C2怎样平移得到的?(4)、设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .26. 如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.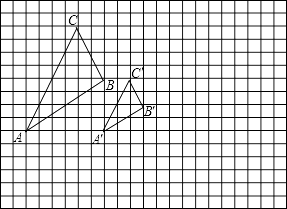 (1)、画出位似中心点O;
(1)、画出位似中心点O;
(2)、直接写出△ABC与△A′B′C′的位似比;
(3)、以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.
27.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′的顶点都在格点上.
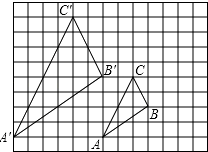 (1)、求证:△ABC∽A′B′C′;(2)、A′B′C′与△ABC是位似图形吗?如果是,在图形上画出位似中心并求出位似比.28.
(1)、求证:△ABC∽A′B′C′;(2)、A′B′C′与△ABC是位似图形吗?如果是,在图形上画出位似中心并求出位似比.28.如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
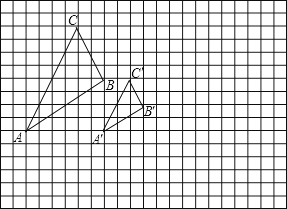 (1)、画出位似中心点O;(2)、直接写出△ABC与△A′B′C′的位似比;(3)、以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.29.
(1)、画出位似中心点O;(2)、直接写出△ABC与△A′B′C′的位似比;(3)、以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.29.如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.
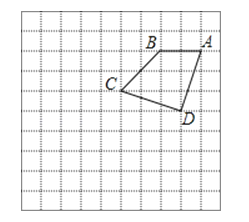 (1)、在图中画出四边形AB′C′D′;
(1)、在图中画出四边形AB′C′D′;
(2)、填空:△AC′D′是 三角形.