备考2022年中考数学一轮复习(湘教版)专题60 正弦和余弦、正切
试卷更新日期:2021-09-23 类型:一轮复习
一、单选题
-
1. 若用我们数学课本上采用的科学计算器计算sin36 18',按键顺序正确的是( )A、
 B、
B、 C、
C、 D、
D、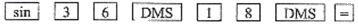 2. 如图,在 中, , , ,若用科学计算器求AC的长,则下列按键顺序正确的是( )
2. 如图,在 中, , , ,若用科学计算器求AC的长,则下列按键顺序正确的是( )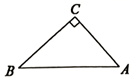 A、 B、 C、 D、3. 若规定 ,则sin15°=( )A、 B、 C、 D、4. 已知 为锐角,且 ,则 等于( )A、 B、 C、 D、5. 如图,A,B,C是3×1的正方形网格中的三个格点,则 tan∠ABC的值为( )
A、 B、 C、 D、3. 若规定 ,则sin15°=( )A、 B、 C、 D、4. 已知 为锐角,且 ,则 等于( )A、 B、 C、 D、5. 如图,A,B,C是3×1的正方形网格中的三个格点,则 tan∠ABC的值为( ) A、 B、 C、 D、6. 如图,在 中, ,则 的值为( )
A、 B、 C、 D、6. 如图,在 中, ,则 的值为( )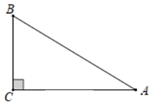 A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
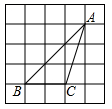
7. 在Rt△ABC中,∠C=90°,AC=3,BC=4,则tanA=.8. 计算: .9. 比较大小:2sin60°+tan45° 4cos60° (用“>”或“=”或“<”连接).10. 如图,△ABC的顶点是正方形网格的格点,则tanA的值为.
 11. 如图,在Rt△ABC中,∠C=90°,AB= 5,AC= 4,则cosA= .
11. 如图,在Rt△ABC中,∠C=90°,AB= 5,AC= 4,则cosA= .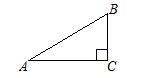 12. 如图所示的网格是边长为1的正方形网格, , , 是网格线交点,则 .
12. 如图所示的网格是边长为1的正方形网格, , , 是网格线交点,则 .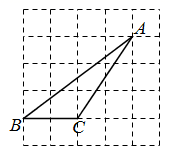
三、计算题
-
13. 计算:2sin30°+cos30°•tan60°.14. 计算:2cos60°+4sin60° tan30°-6cos245°.15. 计算:3tan30°﹣2sin60°+cos245°.16. 计算:(1)、(2)、(3)、
四、解答题
-
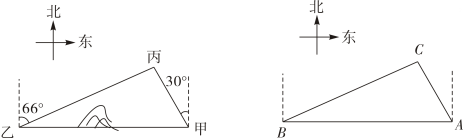
17. 如图,已知甲地在乙地的正东方向,因有大山阻隔,由甲地到乙地需要绕行丙地.已知丙地位于甲地北偏西 方向,距离甲地 ,丙地位于乙地北偏东 方向,现要打通穿山隧道,建成甲乙两地直达高速公路,如果将甲、乙、丙三地当作三个点 ,可抽象成右图所示的三角形,求甲乙两地之间直达高速线路的长 (结果用含非特殊角的三角函数和根式表示即可).
 18. 两栋居民楼之间的距离 ,楼 和 均为10层,每层楼高为 .上午某时刻,太阳光线 与水平面的夹角为30°,此刻楼 的影子会遮挡到楼 的第几层?(参考数据: , )
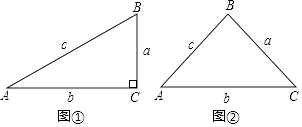
18. 两栋居民楼之间的距离 ,楼 和 均为10层,每层楼高为 .上午某时刻,太阳光线 与水平面的夹角为30°,此刻楼 的影子会遮挡到楼 的第几层?(参考数据: , )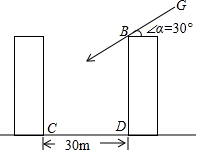 19. 如图①,在Rt△ABC中,以下是小亮探究 与 之间关系的方法:
19. 如图①,在Rt△ABC中,以下是小亮探究 与 之间关系的方法:∵sinA= ,sinB= ,
∴c= ,c= ,
∴ = ,
根据你掌握的三角函数知识.在图②的锐角△ABC中,探究 、 、 之间的关系,并写出探究过程.
 20. 小明在某次作业中得到如下结果:
20. 小明在某次作业中得到如下结果:sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°≈( )2+( )2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
五、综合题
-
21. 若 ( 为锐角).(1)、求 的值;(2)、计算: .22. 如图,根据图中数据完成填空,再按要求答题:
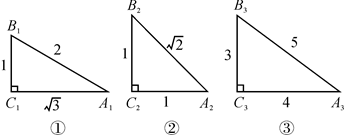 (1)、sin2A1+sin2B1=;sin2A2+sin2B2=;sin2A3+sin2B3=;(2)、观察上述等式,猜想:在Rt△ABC中,∠C=90°.都有:sin2A+sin2B=;(3)、如图,在Rt△ABC中,∠C=90°,∠A , ∠B , ∠C的对边分别是a , b , c;利用三角函数的定义和勾股定理,证明你的猜想;
(1)、sin2A1+sin2B1=;sin2A2+sin2B2=;sin2A3+sin2B3=;(2)、观察上述等式,猜想:在Rt△ABC中,∠C=90°.都有:sin2A+sin2B=;(3)、如图,在Rt△ABC中,∠C=90°,∠A , ∠B , ∠C的对边分别是a , b , c;利用三角函数的定义和勾股定理,证明你的猜想;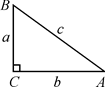 (4)、已知:∠A+∠B=90°,且sinA= , 求sinB.
(4)、已知:∠A+∠B=90°,且sinA= , 求sinB.