备考2022年中考数学一轮复习(湘教版)专题54 中心对称和中心对称图形
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
1. 以下有关勾股定理证明的图形中,不是中心对称图形的是( )A、
 B、
B、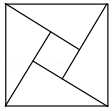 C、
C、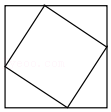 D、
D、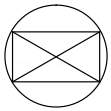 2. 下列四个图案中,是中心对称图形的是( )A、
2. 下列四个图案中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 如图是 的网格图,将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是( )
3. 如图是 的网格图,将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是( )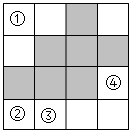 A、① B、② C、③ D、④4. 下列图形中,是中心对称图形的是( )A、
A、① B、② C、③ D、④4. 下列图形中,是中心对称图形的是( )A、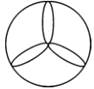 B、
B、 C、
C、 D、
D、 5. 如图,在平面直角坐标系中,多边形 的顶点坐标分别是 , , , , 和 .若直线 将多边形 分割成面积相等的两部分,则 ( )
5. 如图,在平面直角坐标系中,多边形 的顶点坐标分别是 , , , , 和 .若直线 将多边形 分割成面积相等的两部分,则 ( ) A、 B、 C、4 D、36. 下列图形中是中心对称图形的是( )A、
A、 B、 C、4 D、36. 下列图形中是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 下列图形中,是中心对称图形的是( )A、
7. 下列图形中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
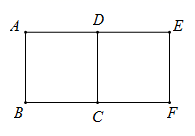
D、 8. 如图,点O为矩形 的对称中心,点E从点A出发沿 向点B运动到点B停止,延长 交 于点F,则四边形 形状的变化依次为( )
8. 如图,点O为矩形 的对称中心,点E从点A出发沿 向点B运动到点B停止,延长 交 于点F,则四边形 形状的变化依次为( ) A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形-菱形→矩形 D、正方形→菱形→平行四边形→矩形9. 将一个等腰三角形沿底边上的中线剪开,用剪下的两个三角形拼成的所有四边形中,是中心对称图形的有( ).A、1个 B、2个 C、3个 D、4个
A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形-菱形→矩形 D、正方形→菱形→平行四边形→矩形9. 将一个等腰三角形沿底边上的中线剪开,用剪下的两个三角形拼成的所有四边形中,是中心对称图形的有( ).A、1个 B、2个 C、3个 D、4个二、填空题
-
10. 若点A与点B(1,1)关于点C(-1,-1)对称,则点A的坐标是.11. 如图,正方形ABCD旋转后能与正方形CDEF重合,那么点A,B,C,D中,可以作为旋转中心的有个.
 12. 如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为 .
12. 如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为 .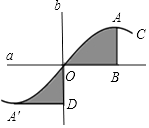 13. 请写出一个是中心对称图形的几何图形的名称: .14. 下面图形:四边形,三角形,梯形,平行四边形,菱形,矩形,正方形,圆,从中任取一个图形既是轴对称图形又是中心对称图形的概率是 .15. 3个边长为1的小正方形拼成的图形如图所示,P是其中两个小正方形的公共顶点,且点A,B,P三点共线,现将该图形沿着过点P的某条直线剪一刀,使剪痕两侧的面积相等,则剪痕的长度是。
13. 请写出一个是中心对称图形的几何图形的名称: .14. 下面图形:四边形,三角形,梯形,平行四边形,菱形,矩形,正方形,圆,从中任取一个图形既是轴对称图形又是中心对称图形的概率是 .15. 3个边长为1的小正方形拼成的图形如图所示,P是其中两个小正方形的公共顶点,且点A,B,P三点共线,现将该图形沿着过点P的某条直线剪一刀,使剪痕两侧的面积相等,则剪痕的长度是。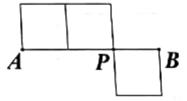 16. 将△ABC绕着C(1,0)旋转180°得到△A1B1C , 设点A的坐标为(a , b),则点A1的坐标为
16. 将△ABC绕着C(1,0)旋转180°得到△A1B1C , 设点A的坐标为(a , b),则点A1的坐标为三、作图题
-
17. 如图,两个任意四边形中心对称,请找出它们的对称中心.
 18. 图甲,图乙是两张完全相同的8×6方格纸,方格纸中每个小正方形的边长均为1,点A,B,C均位于格点处,请按要求画出格点四边形(四边形各顶点都在格点上).(均只需在答题卡上画出一种)
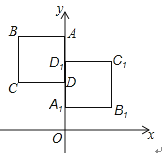
18. 图甲,图乙是两张完全相同的8×6方格纸,方格纸中每个小正方形的边长均为1,点A,B,C均位于格点处,请按要求画出格点四边形(四边形各顶点都在格点上).(均只需在答题卡上画出一种) (1)、在图甲中画出一个以点A,B,C,P为顶点的格点四边形,且为中心对称图形.(2)、在图乙中画出一个以点A,B,C,P为顶点的格点四边形,CA平分∠BCP,且有两个内角均为90°.19. 如图所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系四边形 的顶点A的坐标为 ,顶点B的坐标为 ,顶点C的坐标为 ,请在图中画出四边形 关于原点 .对称的四边形 .
(1)、在图甲中画出一个以点A,B,C,P为顶点的格点四边形,且为中心对称图形.(2)、在图乙中画出一个以点A,B,C,P为顶点的格点四边形,CA平分∠BCP,且有两个内角均为90°.19. 如图所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系四边形 的顶点A的坐标为 ,顶点B的坐标为 ,顶点C的坐标为 ,请在图中画出四边形 关于原点 .对称的四边形 . 20. 如图,在方格网中已知格点△ABC和点O,画出 使得 与△ABC关于点O成中心对称.
20. 如图,在方格网中已知格点△ABC和点O,画出 使得 与△ABC关于点O成中心对称. 21. 由16个边长相等的小正方形组成的图形如图所示,请你用一条割线(可以是折线)将它分割成两个图形,使之关于某一点成中心对称,要求给出两种不同的方法.
21. 由16个边长相等的小正方形组成的图形如图所示,请你用一条割线(可以是折线)将它分割成两个图形,使之关于某一点成中心对称,要求给出两种不同的方法. 22. 如图,作出△ABC关于点O成中心对称的三角形.(保留作图痕迹)
22. 如图,作出△ABC关于点O成中心对称的三角形.(保留作图痕迹)
四、解答题
-
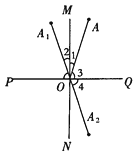
23. 已知MN⊥PQ于点O,点A1和点A关于MN对称,点A2和点A关于PQ对称,试证明:点A1和点A2关于点O成中心对称.
24. 下列图形是中心对称图形吗?如果是中心对称图形,在图中用点O标出对称中心.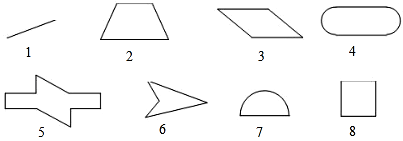 25. 如图,已知△ABC与△A′B′C′成中心对称图形,求出它的对称中心O.
25. 如图,已知△ABC与△A′B′C′成中心对称图形,求出它的对称中心O.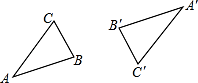 26. 如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
26. 如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.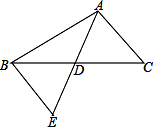 (1)、图中哪两个图形成中心对称?(2)、若△ADC的面积为4,求△ABE的面积.27.
(1)、图中哪两个图形成中心对称?(2)、若△ADC的面积为4,求△ABE的面积.27.已知点A的坐标为( ,0),把点A绕着坐标原点顺时针旋转135º到点B,求点B的坐标.
五、综合题
-
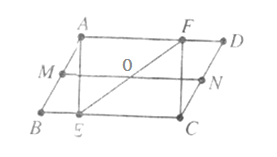
28. 如图所示,△DEF是由△ABC绕点O顺时针旋转180°后形成的图形;
 (1)、请你指出图中所有相等的线段;
(1)、请你指出图中所有相等的线段;
(2)、图中哪些三角形可以被看成是关于点O成中心对称关系?
29. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣4,2)、B(0,4)、C(0,2), (1)、画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(1)、画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)、△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
30.如图,△ABC的三个顶点都在格点上,每个小方格边长均为1个单位长度,建立如图坐标系.
 (1)、请你作出△ABC关于点A成中心对称的△AB1C1(其中B的对称点是B1 , C的对称点是C1),并写出点B1、C1的坐标.(2)、依次连接BC1、C1B1、B1C.猜想四边形BC1B1C是什么特殊四边形?并说明理由.
(1)、请你作出△ABC关于点A成中心对称的△AB1C1(其中B的对称点是B1 , C的对称点是C1),并写出点B1、C1的坐标.(2)、依次连接BC1、C1B1、B1C.猜想四边形BC1B1C是什么特殊四边形?并说明理由.