备考2022年中考数学一轮复习（湘教版）专题56 简单图形、轴对称和平移的坐标表示

试卷更新日期：2021-09-22 类型：一轮复习

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，将点A（-3，-2）向右平移5个单位长度得到点B，则点B关于y轴对称点B’的坐标为（）

A、（2，2） B、（-2，2） C、（-2，-2） D、（2，-2）

查看试题解析
2. 在平面直角坐标系中，将点P（3，2）向上平移2个单位长度，得到的点的坐标是（）

A、（3，4） B、（1，2） C、（5，2） D、（3 ，0）

查看试题解析
3. 将点 $A (2 ， - 3)$ 沿x轴向左平移3个单位长度后得到的点 $A^{'}$ 的坐标为（）

A、 $(- 1 ， - 6)$ B、 $(2 ， - 6)$ C、 $(- 1 ， - 3)$ D、 $(5 ， - 3)$

查看试题解析
4. 在平面直角坐标系中，将点A（-1，2）向下平移3个单位长度，再向右平移2个单位长度，得到点A′，则点A′的坐标是（）

A、（-3，-1） B、（1，-1） C、（-1，1） D、（-4，4）

查看试题解析
5. 已知平面直角坐标系中点 $P (- 3 ， 4)$ .将它沿 $y$ 轴方向向上平移3个单位所得点的坐标是（）

A、 $(- 3 ， 1)$ B、 $(- 3 ， 7)$ C、 $(0 ， 4)$ D、 $(- 6 ， 4)$

查看试题解析
6. 四盏灯笼的位置如图．已知A ， B ， C ， D的坐标分别是（﹣1，b），（1，b），（2，b），（3，5，b），平移y轴右侧的一盏灯笼，使得y轴两侧的灯笼对称，则平移的方法可以是（）

A、将B向左平移4.5个单位 B、将C向左平移4个单位 C、将D向左平移5.5个单位 D、将C向左平移3.5个单位

查看试题解析
7. 如图，在平面直角坐标系中，已知点 $M (2 ， 1)$ ， $N (1 ， - 1)$ ，平移线段 $M N$ ，使点 $M$ 落在点 $M^{'} (- 1 ， 2)$ 处，则点 $N$ 对应的点 $N^{'}$ 的坐标为（）

A、 $(- 2 ， 0)$ B、 $(0 ， - 2)$ C、 $(- 1 ， 1)$ D、 $(- 3 ， - 1)$

查看试题解析
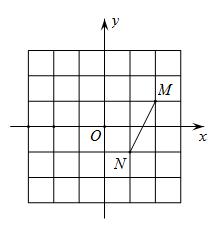8. 在平面直角坐标系中，点 $P (- 3, 2)$ 关于 $x$ 轴对称的点的坐标是（）

A、 $(3, 2)$ B、 $(2, - 3)$ C、 $(- 3, 2)$ D、 $(- 3, - 2)$

查看试题解析
9. 点 $P (3, - 5)$ 关于y轴的对称点是（）

A、 $(- 3, 5)$ B、 $(3, 5)$ C、 $(- 3, - 5)$ D、 $(3, - 5)$

查看试题解析

二、填空题

10. 点 $P (2 ， 3)$ 关于 $x$ 轴对称的点 $P^{'}$ 的坐标是．

查看试题解析
11. 若点 $A (1 + m ， 1 - n)$ 与点 $B (- 3 ， 2)$ 关于 $y$ 轴对称，则 ${(m + n)}^{2021} =$ 值是.

查看试题解析
12. 矩形ABCD中，A（﹣3，2），B（0，2），C（0，3），则点D坐标为.

查看试题解析
13. 如图，在平面直角坐标系中，将点 $A (- 1 ， 2)$ 向右平移2个单位长度得到点 $B$ ，则点 $B$ 关于 $x$ 轴的对称点 $C$ 的坐标是.

查看试题解析
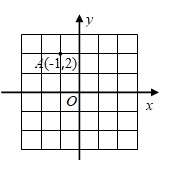14. 点(2，3)关于y轴对称的点的坐标为．

查看试题解析
15. 点A的坐标是（2，﹣3），将点A向上平移4个单位长度得到点A'，则点A'的坐标为.

查看试题解析

三、解答题

16.
在平面直角坐标系中指出下列各点A（5，1），B（5，0），C（2，1），D（2，3），并顺次连接，且将所得图形向下平移3个单位，写出对应点A′、B′、C′、D′的坐标．

查看试题解析
17.
如图所示，△ABC和△A′BC存在着某种对应关系（它们关于BC对称），其中A的对应点是A′，A（3，6），A′（3，0），△ABC内部的点M（4，4）的对应点是N（4，2）．
（1）你知道它们的对应点的坐标有什么关系吗？
（2）如果△ABC内有一点P（x，y），那么在△A′BC内P的对应点P′的坐标是什么？

查看试题解析
18. 已知点A（2x+y，﹣7）与点B（4，4y﹣x）关于x轴对称，试求（x+y）的值．

查看试题解析
19. 在平面直角坐标系中，已知点A（﹣2，﹣3）关于x轴对称的点为B，关于y轴对称的点为C，求△ABC的面积．

查看试题解析

四、综合题

20.
如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣4，3）、B（﹣3，1）、C（﹣1，3）．

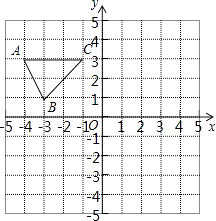(1)、请按下列要求画图：
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度，得到△A₁B₁C₁ ，画出△A₁B₁C₁；
②△A₂B₂C₂与△ABC关于原点O成中心对称，画出△A₂B₂C₂ ．

(2)、在（1）中所得的△A₁B₁C₁和△A₂B₂C₂关于点M成中心对称，请直接写出对称中心M点的坐标．

查看试题解析
21. 如图，在平面直角坐标系中有两点A，B

(1)、尺规作图，在x轴上找一点C，使得AC+BC最小：（尺规作图，不写作法，保留作图痕迹）；

(2)、若A的坐标为（﹣2，1），B的坐标为（3，5）在x轴上找一点C，使得AC+BC最小，求点C的坐标．

查看试题解析
22.
如图，已知△ABC的顶点A，B，C的坐标分别是A（﹣1，﹣1），B（﹣4，﹣3），C（﹣4，﹣1）．

(1)、作出△ABC关于原点O中心对称的图形；

(2)、将△ABC绕原点O按顺时针方向旋转90°后得到△A₁B₁C₁ ，画出△A₁B₁C₁ ，并写出点A₁的坐标．

查看试题解析
23. 问题情境：
在平面直角坐标系xOy中有不重合的两点A（x₁ ， y₁）和点B（x₂ ， y₂），小明在学习中发现，若x₁＝x₂ ，则AB∥y轴，且线段AB的长度为|y₁﹣y₂|；若y₁＝y₂ ，则AB∥x轴，且线段AB的长度为|x₁﹣x₂|；

(1)、（应用）：
①若点A（﹣1，1）、B（2，1），则AB∥x轴，AB的长度为.

②若点C（1，0），且CD∥y轴，且CD＝2，则点D的坐标为.

(2)、（拓展）：
我们规定：平面直角坐标系中任意不重合的两点M（x₁ ， y₁），N（x₂ ， y₂）之间的折线距离为d（M，N）＝|x₁﹣x₂|+|y₁﹣y₂|；例如：图1中，点M（﹣1，1）与点N（1，﹣2）之间的折线距离为d（M，N）＝|﹣1﹣1|+|1﹣（﹣2）|＝2+3＝5.

解决下列问题：

①如图1，已知E（2，0），若F（﹣1，﹣2），则d（E，F）；

②如图2，已知E（2，0），H（1，t），若d（E，H）＝3，则t＝.

③如图3，已知P（3，3），点Q在x轴上，且三角形OPQ的面积为3，则d（P，Q）＝.

查看试题解析
24. 如图，在平面直角坐标系中，给出如下定义：已知点A（2，3），点B（6，3），连接AB．如果线段AB上有一个点与点P的距离不大于1，那么称点P是线段AB的“环绕点”．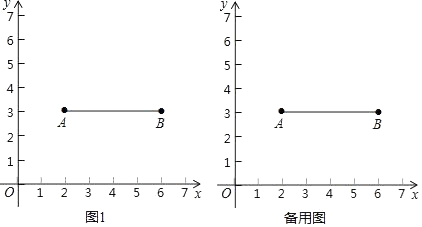

(1)、已知点C（3，1.5），D（4，3.5），E（1，3），则是线段AB的“环绕点”的点是；

(2)、已知点P（m，n）在反比例函数y= $\frac{8}{x}$ 的图象上，且点P是线段AB的“环绕点”，求出点P的横坐标m的取值范围；

(3)、已知⊙M上有一点P是线段AB的“环绕点”，且点M（4，1），求⊙M的半径r的取值范围．

查看试题解析