备考2022年中考数学一轮复习（湘教版）专题57 比例线段与平行线分线段成比例

试卷更新日期：2021-09-22 类型：一轮复习

进入出卷网下载

一、单选题

1. 两千多年前，古希腊数学家欧多克索斯发现了黄金分割，即：如图，点P是线段AB上一点（AP＞BP），若满足 $\frac{B P}{A P} = \frac{A P}{A B}$ ，则称点P是AB的黄金分割点.黄金分割在日常生活中处处可见，例如：主持人在舞台上主持节目时，站在黄金分割点上，观众看上去感觉最好.若舞台长20米，主持人从舞台一侧进入，设他至少走x米时恰好站在舞台的黄金分割点上，则x满足的方程是（）

A、（20﹣x）²＝20x B、x²＝20（20﹣x） C、x（20﹣x）＝20² D、以上都不对

查看试题解析
2. 如图，在菱形ABCD中，点E ， F分别在AB ， CD上，且BE＝2AE ， DF＝2CF ，点G ， H分别是AC的三等分点，则S_{四边形EHFG}÷S_菱形ABCD的值为（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{2}{9}$

查看试题解析
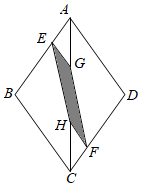3. 如图，直线l₁∥l₂∥l₃ ，直线AC和DF被l₁ ， l₂ ， l₃所截，AB＝5，BC＝6，EF＝4，则DE的长为（）

A、2 B、3 C、4 D、 $\frac{10}{3}$

查看试题解析
4. 若9x=5y，则 $\frac{x}{y}$ =（）

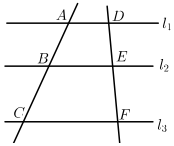A、 $\frac{9}{5}$ B、 $\frac{5}{9}$ C、 $\frac{9}{4}$ D、 $\frac{4}{9}$

查看试题解析
5. 如图，四边形ABCD是平行四边形，点E在CD边上，则下列结论错误的是（）

A、 $\frac{A F}{F E} = \frac{B F}{F D}$ B、 $\frac{D E}{A B} = \frac{D F}{B D}$ C、 $\frac{A F}{A E} = \frac{B F}{B D}$ D、 $\frac{D E}{D C} = \frac{E F}{A F}$

查看试题解析
6. 如图，AB//CD//EF ，下列等式成立的是（）

A、AC·CE=BD·DF B、AC·AE=BD·BF C、AC·DF=CE·BD D、CD²=AB·EF

查看试题解析

二、填空题

7. 如图是一架梯子的示意图，其中AA₁∥BB₁∥CC₁∥DD₁ ，且AB＝BC＝CD.为使其更稳固，在A，D₁间加绑一条安全绳（线段AD₁）量得AE＝0.4m，则AD₁＝m.

查看试题解析
8. 已知 $\frac{x}{2} = \frac{y}{3} = \frac{z}{4} \neq 0$ ，则 $\frac{x^{2} + x y}{y z} =$

查看试题解析
9. 如图，△ABC中，D、F在AB边上，E、G在AC边上，DE∥FG∥BC，且AD：DF：FB＝3：2：1，若AG＝15，则EC的长为.

查看试题解析
10. 已知点 $P$ 在线段 $A B$ 上，如果 $A P^{2} = A B \cdot B P$ ， $A B = 4$ ，那么 $A P$ 的长是．

查看试题解析
11. 如图，点A、B在双曲线y＝ $\frac{k}{x}$ （x＞0）上，点C、D在坐标轴上，AC⊥x轴，BD⊥y轴，OA与BD交于点E，OB与AC交于点F，AC与DB交于点G，BD＝2OC，四边形OEGF的面积为2，则k的值为．

查看试题解析
12. 如图，在△ABC中，DE $/ /$ AB，CD：DA=2：3，DE=4，则AB的长为．

查看试题解析

三、解答题

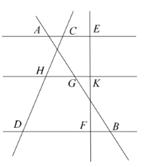
13. 已知直线l₁∥l₂∥l₃ ， AG=1.2cm，BG=2.4cm，EF=3cm，CD=4cm，求CH、KF的值。

查看试题解析
14. 在一张比例尺为 $1 : 20$ 的地图上，有一块多边形区域的周长是 $24 cm$ ，面积是 $20 {cm}^{2}$ ，求这个区域的实际周长和面积．

查看试题解析
15.
深圳市民中心广场上有旗杆如图①所示，某学校数学兴趣小组测量了该旗杆的高度.如图②，某一时刻，旗杆AB的影子一部分落在平台上，另一部分落在斜坡上，测得落在平台上的影长BC为16米，落在斜坡上的影长CD为8米，AB⊥BC；同一时刻，太阳光线与水平面的夹角为 45°，1米的标杆EF竖立在斜坡上的影长FG为2米，求旗杆的高度.

查看试题解析
16.
如图，在△ABC中，点D，E分别在边AB，AC上，若DE∥BC，AD=3，AB=5，求 $\frac{D E}{B C}$ 的值．

查看试题解析
17. 如图，直线 $a / / b / / c$ ，直线 $m ， n$ 相交于点 $O$ ，且分别与直线 $a ， b ， c$ 相交于点 $A ， B ， C$ 和点 $D ， E ， F$ ，已知 $O A = 3$ ， $O B = 4$ ， $B C = 6$ ， $E F = 5$ ，求 $D O$ 的长度．

查看试题解析

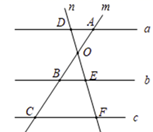
四、综合题

18. 如图，△ABC中，∠ACB=90°，AC=5，BC=12，CO⊥AB于点O，D是线段OB上一点，DE=2，ED∥AC（∠ADE＜90°），连接BE、CD．设BE、CD的中点分别为P、Q．

(1)、求AO的长；

(2)、求PQ的长；

(3)、设PQ与AB的交点为M，请直接写出|PM﹣MQ|的值．

查看试题解析
19.

(1)、如图1，Rt△ABC中，∠B=90°，AB=2BC，现以C为圆心、CB长为半径画弧交边AC于D，再以A为圆心、AD为半径画弧交边AB于E．求证： $\frac{A E}{A B}$ = $\frac{\sqrt{5} - 1}{2}$ ．（这个比值 $\frac{\sqrt{5} - 1}{2}$ 叫做AE与AB的黄金比．）

(2)、如果一等腰三角形的底边与腰的比等于黄金比，那么这个等腰三角形就叫做黄金三角形．请你以图2中的线段AB为腰，用直尺和圆规，作一个黄金三角形ABC．
（注：直尺没有刻度！作图不要求写作法，但要求保留作图痕迹，并对作图中涉及到的点用字母进行标注）

查看试题解析
20. 如图，直线 $l_{1} ∥ l_{2} ∥ l_{3}$ ，AC分别交 $l_{1} ，_{}^{} l_{2} ，_{}^{} l_{3}$ 于点A，B，C；DF分别交 $l_{1} ，_{}^{} l_{2} ，_{}^{} l_{3}$ 于点D，E，F；AC与DF交于点O.已知DE=3，EF=6，AB=4.

(1)、求AC的长；

(2)、若BE：CF=1：3，求OB：AB.

查看试题解析
21. 如图，在 $△ A B C$ 中，BE平分 $∠ A B C$ 交AC于点E，过点E作 $E D ∥ B C$ 交AB于点D，已知 $A D = 5$ ， $B D = 4$ ．

(1)、求BC的长度；

(2)、如果 $\overset{⇀}{A D} = \overset{⇀}{a}$ ， $\overset{⇀}{A E} = \overset{⇀}{b}$ ，那么请用 $\overset{⇀}{a}$ 、 $\overset{⇀}{b}$ 表示向量 $\overset{⇀}{C B}$ ．

查看试题解析
22. 已知三条线段 $a, b, c$ 满足 $\frac{a}{3} = \frac{b}{2} = \frac{c + 1}{4}$ ，且 $a + b + c = 17$ .

(1)、求 $a, b, c$ 的值；

(2)、若线段 $d$ 是线段 $a$ 和 $b$ 的比例中项，求 $d$ 的值.

查看试题解析