备考2022年中考数学一轮复习(湘教版)专题53 轴对称与旋转
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
1. 如图,在平面内将五角星绕其中心旋转180°后所得到的图案是( )
 A、
A、 B、
B、 C、
C、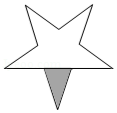 D、
D、 2. 下列图形是轴对称图形的是( )A、
2. 下列图形是轴对称图形的是( )A、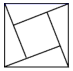 B、
B、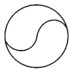 C、
C、 D、
D、 3. 以下四个标志,每个标志都有图案和文字说明,其中的图案是轴对称图形是( )A、
3. 以下四个标志,每个标志都有图案和文字说明,其中的图案是轴对称图形是( )A、 B、
B、 C、
C、 D、
D、 4. 已知在 中, , .点 为边 上的动点,点 为边 上的动点,则线段 的最小值是( )
4. 已知在 中, , .点 为边 上的动点,点 为边 上的动点,则线段 的最小值是( ) A、 B、 C、 D、5. 如图,△AOB中,OA=4,OB=6,AB=2 ,将△AOB绕原点O旋转90°,则旋转后点A的对应点A′的坐标是( )
A、 B、 C、 D、5. 如图,△AOB中,OA=4,OB=6,AB=2 ,将△AOB绕原点O旋转90°,则旋转后点A的对应点A′的坐标是( )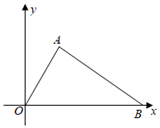 A、(4,2)或(﹣4,2) B、(2 ,﹣4)或(﹣2 ,4) C、(﹣2 ,2)或(2 ,﹣2) D、(2,﹣2 )或(﹣2,2 )6. 如图,将 绕点 逆时针旋转 得到 ,若 且 于点 ,则 的度数为( )
A、(4,2)或(﹣4,2) B、(2 ,﹣4)或(﹣2 ,4) C、(﹣2 ,2)或(2 ,﹣2) D、(2,﹣2 )或(﹣2,2 )6. 如图,将 绕点 逆时针旋转 得到 ,若 且 于点 ,则 的度数为( ) A、 B、 C、 D、7. 如图,在 中, , ,将 绕点C顺时针旋转90°得到 ,点B的对应点 在边 上(不与点A , C重合),则 的度数为( )
A、 B、 C、 D、7. 如图,在 中, , ,将 绕点C顺时针旋转90°得到 ,点B的对应点 在边 上(不与点A , C重合),则 的度数为( )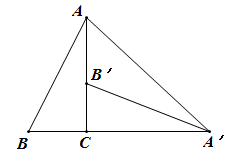 A、 B、 C、 D、8. 如图是用七巧板拼接成的一个轴对称图形(忽略拼接线),小亮改变①的位置,将①分别摆放在图中左,下,右的位置(摆放时无缝隙不重叠),还能拼接成不同轴对称图形的个数为( )
A、 B、 C、 D、8. 如图是用七巧板拼接成的一个轴对称图形(忽略拼接线),小亮改变①的位置,将①分别摆放在图中左,下,右的位置(摆放时无缝隙不重叠),还能拼接成不同轴对称图形的个数为( )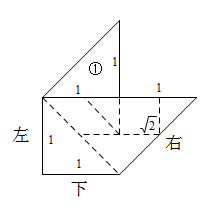 A、2 B、3 C、4 D、59. 如图,在 中, ,将 绕点C逆时针旋转得到 ,点A,B的对应点分别为D,E,连接 .当点A,D,E在同一条直线上时,下列结论一定正确的是( )
A、2 B、3 C、4 D、59. 如图,在 中, ,将 绕点C逆时针旋转得到 ,点A,B的对应点分别为D,E,连接 .当点A,D,E在同一条直线上时,下列结论一定正确的是( )
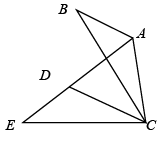 A、 B、 C、 D、10. 如图,直线 , 相交于点 . 为这两直线外一点,且 .若点 关于直线 , 的对称点分别是点 , ,则 , 之间的距离可能是( )
A、 B、 C、 D、10. 如图,直线 , 相交于点 . 为这两直线外一点,且 .若点 关于直线 , 的对称点分别是点 , ,则 , 之间的距离可能是( ) A、0 B、5 C、6 D、7
A、0 B、5 C、6 D、7二、填空题
-
11. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,连接 ,若将 绕点 顺时针旋转 ,得到 ,则点 的坐标为 .
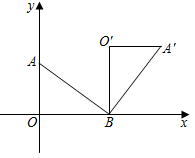 12. 如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为4cm2 , ∠AOB=120°,则图中阴影部分的面积为 .
12. 如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为4cm2 , ∠AOB=120°,则图中阴影部分的面积为 . 13. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C分别在x轴,y轴上,B,D两点坐标分别为B(﹣4,6),D(0,4),线段EF在边OA上移动,保持EF=3,当四边形BDEF的周长最小时,点E的坐标为 .
13. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C分别在x轴,y轴上,B,D两点坐标分别为B(﹣4,6),D(0,4),线段EF在边OA上移动,保持EF=3,当四边形BDEF的周长最小时,点E的坐标为 . 14. 如图,在 中, , , , 为 内一点,则 的最小值为.
14. 如图,在 中, , , , 为 内一点,则 的最小值为. 15. 如图, 是 的边 上的中线,将线段 绕点D顺时针旋转 后,点A的对应点E恰好落在 边上,若 , ,则 的长为.
15. 如图, 是 的边 上的中线,将线段 绕点D顺时针旋转 后,点A的对应点E恰好落在 边上,若 , ,则 的长为.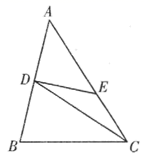 16. 如图,已知点A(2,1),B(0,2),将线段AB绕点M逆时针旋转到A1B1 , 点A与A1是对应点,则点M的坐标是.
16. 如图,已知点A(2,1),B(0,2),将线段AB绕点M逆时针旋转到A1B1 , 点A与A1是对应点,则点M的坐标是.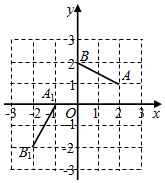 17. 如图,在方格纸上建立的平面直角坐标系中,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△FEC , 则点A的对应点F的坐标是 .
17. 如图,在方格纸上建立的平面直角坐标系中,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△FEC , 则点A的对应点F的坐标是 . 18. 如图,在 中, , , ,若D是 边上的动点,则 的最小值为.
18. 如图,在 中, , , ,若D是 边上的动点,则 的最小值为. 19. 点 关于 轴对称的点 的坐标是 .20. 如右图,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50° ,则∠AEG=度。
19. 点 关于 轴对称的点 的坐标是 .20. 如右图,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50° ,则∠AEG=度。
三、作图题
-
21. 如图,在边长为1的正方形网格中, ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(﹣4,1),点B的坐标为(﹣1,1).

( 1 )画出 ABC绕点B逆时针旋转90°后得到的 A1BC1;并写出A1坐标.
( 2 )画出 ABC关于原点O对称的 A2B2C2.并写出A2坐标.
22. 如图, 的顶点坐标分别为 , , .画出 绕原点O逆时针旋转90°后得到的 ,并写出点 的坐标. 23. 如图,已知ΔABC的三个顶点的坐标分别为A(1,1)、B(2,4)、C(6,2).
23. 如图,已知ΔABC的三个顶点的坐标分别为A(1,1)、B(2,4)、C(6,2).
⑴请画出ΔABC关于x轴对称的图形ΔA1B1C1;
⑵将ΔABC绕坐标原点O逆时针旋转90°, 画出对应图形ΔA2B2C2 , 直接写出点B的对应点B2的坐标;
24. 图①、图②、图③都是 的正方形网格,每个小正方形的顶点称为格点.按下列要求画图:在图①、图②、图③中各画一个以格点为顶点的三角形,要求所画三角形是图中三角形经过轴对称变换后得到的图形,并将所画三角形涂上阴影.(注:所画三角形不能重复)
四、解答题
-
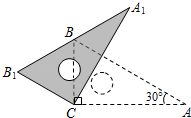
25. 如图,在三角板ABC中,∠ACB=90°,∠A=30°,AC=6,将三角板ABC绕点C逆时针旋转,当起始位置时的点B恰好落在边A1B1上时,求A1B的长
 26.
26.如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(﹣3,5),C(﹣4,1).

①把△ABC向右平移2个单位得△A1B1C1 , 请画出△A1B1C1 , 并写出点A1的坐标;
②把△ABC绕原点O旋转180°得到△A2B2C2 , 请画出△A2B2C2 .
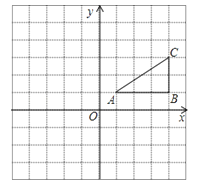
27. 如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).(1)先将Rt△ABC向左平移5个单位长度,再向下平移1个单位长度得到Rt△A1B1C1 , 试在图中画出Rt△A1B1C1 , 并写出点A1的坐标;
(2)再将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2 , 试在图中画出Rt△A2B2C2 , 并计算Rt△A1B1C1在上述旋转过程中点C1所经过的路径长.
 28.
28.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC与△DEF关于点O成中心对称,△ABC与△DEF的顶点均在格点上,请按要求完成下列各题.
(1)在图中画出点O的位置.
(2)将△ABC先向右平移4个单位长度,再向下平移2个单位长度,得到△A1B1C1 , 请画出△A1B1C1;
(3)在网格中画出格点M,使A1M平分∠B1A1C1 .

五、综合题
-
29. 下面是小明关于“对称与旋转的关系”的探究过程,请你补充完整.
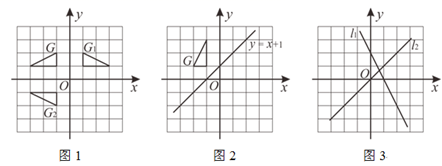 (1)、三角形在平面直角坐标系中的位置如图1所示,简称G , G关于y轴的对称图形为 ,关于 轴的对称图形为 .则将图形 绕点顺时针旋转度,可以得到图形 .(2)、在图2中分别画出G关于y轴和直线 的对称图形 , . 将图形 绕 点(用坐标表示)顺时针旋转 度,可以得到图形 .(3)、综上,如图3,直线 和 所夹锐角为 ,如果图形G关于直线 的对称图形为 ,关于直线 的对称图形为 ,那么将图形 绕点(用坐标表示)顺时针旋转度(用 表示),可以得到图形 .30. 如图①,要在一条笔直的路边l上建一个燃气站,向l同侧的A、B两个城镇分别发铺设管道输送燃气,试确定燃气站的位置,使铺设管道的路线最短.
(1)、三角形在平面直角坐标系中的位置如图1所示,简称G , G关于y轴的对称图形为 ,关于 轴的对称图形为 .则将图形 绕点顺时针旋转度,可以得到图形 .(2)、在图2中分别画出G关于y轴和直线 的对称图形 , . 将图形 绕 点(用坐标表示)顺时针旋转 度,可以得到图形 .(3)、综上,如图3,直线 和 所夹锐角为 ,如果图形G关于直线 的对称图形为 ,关于直线 的对称图形为 ,那么将图形 绕点(用坐标表示)顺时针旋转度(用 表示),可以得到图形 .30. 如图①,要在一条笔直的路边l上建一个燃气站,向l同侧的A、B两个城镇分别发铺设管道输送燃气,试确定燃气站的位置,使铺设管道的路线最短. (1)、如图②,作出点A关于l的对称点 ,线 与直线 的交点C的位置即为所求, 即在点C处建气站, 所得路线ACB是最短的,为了让明点C的位置即为所求,不妨在l直线上另外任取一点 ,连接 , , 证明 , 请完成这个证明.
(1)、如图②,作出点A关于l的对称点 ,线 与直线 的交点C的位置即为所求, 即在点C处建气站, 所得路线ACB是最短的,为了让明点C的位置即为所求,不妨在l直线上另外任取一点 ,连接 , , 证明 , 请完成这个证明.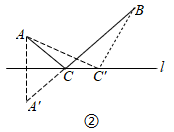 (2)、如果在A、B两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域请分别始出下列两种情形的铺设管道的方案(不需说明理由),
(2)、如果在A、B两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域请分别始出下列两种情形的铺设管道的方案(不需说明理由),①生市保护区是正方形区城,位置如图③所示
②生态保护区是圆形区域,位置如图④所示.
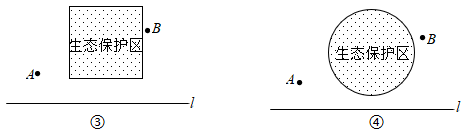 31. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中, 的三个顶点 、 、 均在格点上.
31. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中, 的三个顶点 、 、 均在格点上. (1)、画出 关于 轴对称的 ,并写出点 的坐标;(2)、画出 绕原点 顺时针旋转 后得到的 ,并写出点 的坐标;(3)、在(2)的条件下,求线段 在旋转过程中扫过的面积(结果保留 ).32. 如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(﹣1,3),B(﹣3,1),C(﹣1,1).请解答下列问题:
(1)、画出 关于 轴对称的 ,并写出点 的坐标;(2)、画出 绕原点 顺时针旋转 后得到的 ,并写出点 的坐标;(3)、在(2)的条件下,求线段 在旋转过程中扫过的面积(结果保留 ).32. 如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(﹣1,3),B(﹣3,1),C(﹣1,1).请解答下列问题: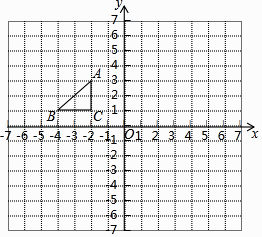 (1)、画出△ABC关于y轴对称的△A1B1C1 , 并写出B1的坐标.(2)、画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C1 , 并求出点A1走过的路径长.
(1)、画出△ABC关于y轴对称的△A1B1C1 , 并写出B1的坐标.(2)、画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C1 , 并求出点A1走过的路径长.