备考2022年中考数学一轮复习(湘教版)专题51 正多边形与圆
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
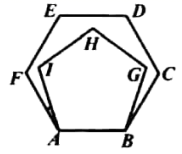
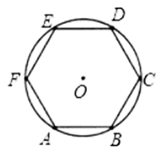
1. 如图所示,在正六边形 内,以 为边作正五边形 ,则 ( )
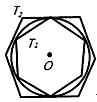
 A、 B、 C、 D、2. 古希腊数学家欧几里得在《几何原本》中记载了用尺规作某种六边形的方法,其步骤是:①在⊙O上任取一点A , 连接AO并延长交⊙O于点B , BO为半径作圆孤分别交⊙O于C , D两点,DO并延长分交⊙O于点E , F;④顺次连接BC , FA , AE , DB , 得到六边形AFCBDE . 连接AD , 交于点G , 则下列结论错误的是 .
A、 B、 C、 D、2. 古希腊数学家欧几里得在《几何原本》中记载了用尺规作某种六边形的方法,其步骤是:①在⊙O上任取一点A , 连接AO并延长交⊙O于点B , BO为半径作圆孤分别交⊙O于C , D两点,DO并延长分交⊙O于点E , F;④顺次连接BC , FA , AE , DB , 得到六边形AFCBDE . 连接AD , 交于点G , 则下列结论错误的是 . A、△AOE的内心与外心都是点G B、∠FGA=∠FOA C、点G是线段EF的三等分点 D、EF= AF3. 如图,正方形的边长为4,剪去四个角后成为一个正八边形,则可求出此正八边形的外接圆直径d , 根据我国魏晋时期数学家刘的“割圆术”思想,如果用此正八边形的周长近似代替其外接圆周长,便可估计的值,下面d及 的值都正确的是( )
A、△AOE的内心与外心都是点G B、∠FGA=∠FOA C、点G是线段EF的三等分点 D、EF= AF3. 如图,正方形的边长为4,剪去四个角后成为一个正八边形,则可求出此正八边形的外接圆直径d , 根据我国魏晋时期数学家刘的“割圆术”思想,如果用此正八边形的周长近似代替其外接圆周长,便可估计的值,下面d及 的值都正确的是( ) A、 , B、 , C、 , D、 ,4. 如图,正五边形 中, 的度数为( )
A、 , B、 , C、 , D、 ,4. 如图,正五边形 中, 的度数为( ) A、 B、 C、 D、5. 下列多边形中,内角和最大的是( )A、
A、 B、 C、 D、5. 下列多边形中,内角和最大的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,AC是正五边形ABCDE的对角线,∠ACD的度数是( )
6. 如图,AC是正五边形ABCDE的对角线,∠ACD的度数是( )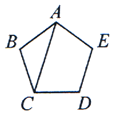 A、72° B、36° C、74° D、88°
A、72° B、36° C、74° D、88°二、填空题
-
7. 边长为 的正六边形,它的外接圆与内切圆半径的比值是 .8. 六个带 角的直角三角板拼成一个正六边形,直角三角板的最短边为1,求中间正六边形的面积 .
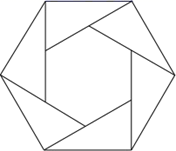 9. 如图,正五边形 内接于 ,点 在弧 上,则 的度数为
9. 如图,正五边形 内接于 ,点 在弧 上,则 的度数为 10. 如图,正五边形 内接于 ,F是 的中点,则 的度数为.
10. 如图,正五边形 内接于 ,F是 的中点,则 的度数为.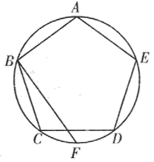 11. 正十边形的每一个内角的度数为.12. 如图,正方形 和正六边形 均内接于 ,连接 ;若线段 恰好是 的一个内接正 边形的一条边,则 .
11. 正十边形的每一个内角的度数为.12. 如图,正方形 和正六边形 均内接于 ,连接 ;若线段 恰好是 的一个内接正 边形的一条边,则 .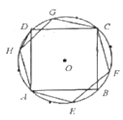
三、解答题
-
13. 一个正多边形的一个内角的度数比相邻外角的6倍还多12°,求这个正多边形的内角和.14. 如图,已知圆O内接正六边形 的边长为 ,求这个正六边形的边心距n , 面积S .
 15. 如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为( ) ,正六边形的边长为( )cm(其中 ),求这两段铁丝的总长
15. 如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为( ) ,正六边形的边长为( )cm(其中 ),求这两段铁丝的总长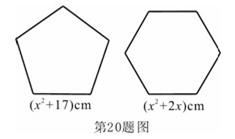
四、综合题
-
16. 圆周率 的故事
我国古代数学家刘徽通过“割圆术”来估计圆周率 的值——“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”,可以理解为当正多边形的边数越来越多时,该正多边形与它的外接圆越来越“接近”,这样就可以用正多边形的周长替代它的外接圆的周长,从而估算出圆周率 的值.
(1)、对于边长为a的正方形,其外接圆半径为 , 根据故事中的方法,用该正方形的周长4a替代它的外接圆周长,利用公式 ,可以估算 .(2)、类比(1),当正多边形为正六边形时,估计 的值.17. 如图,正五边形ABCD中,点F、G分别是BC、CD的中点,AF与BG相交于H.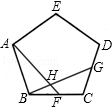 (1)、求证:△ABF≌△BCG;(2)、求∠AHG的度数.
(1)、求证:△ABF≌△BCG;(2)、求∠AHG的度数.