备考2022年中考数学一轮复习(湘教版)专题50 弧长和扇形面积
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
1. 已知圆锥的母线长为3,底面圆半径为1,则圆锥侧面展开图的圆心角为( )A、30° B、60° C、120° D、150°2. 若扇形的半径为3,圆心角为60°,则此扇形的弧长是( )A、 π B、π C、 π D、2π3. 一条弧所对的圆心角为135°,弧长等于半径为3cm的圆的周长的5倍,则这条弧的半径为( )A、45cm B、40cm C、35cm D、30cm4. 已知扇形的半径为6,圆心角为 .则它的面积是( )A、 B、 C、 D、5. 如图,正六边形 的边长为6,以顶点A为圆心, 的长为半径画圆,则图中阴影部分的面积为( )
 A、 B、 C、 D、6. 一个几何体的三视图如图所示,则这个几何体的侧面积是( )
A、 B、 C、 D、6. 一个几何体的三视图如图所示,则这个几何体的侧面积是( )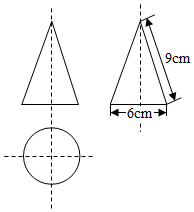 A、 B、 C、 D、7. 一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若 ,则劣弧AB的长是( )
A、 B、 C、 D、7. 一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若 ,则劣弧AB的长是( )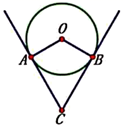 A、 B、 C、 D、8. 如图,等边 的三个顶点都在 上, 是 的直径.若 ,则劣弧 的长是( )
A、 B、 C、 D、8. 如图,等边 的三个顶点都在 上, 是 的直径.若 ,则劣弧 的长是( )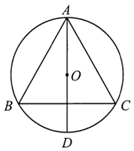 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若母线长 为 ,扇形的圆心角 ,则圆锥的底面圆半径 为 .
 10. 圆锥的母线长为 ,底面圆的半径长为 ,则该圆锥的侧面积为 .11. 如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为 cm,侧面积为 ,则这个扇形的圆心角的度数是度.
10. 圆锥的母线长为 ,底面圆的半径长为 ,则该圆锥的侧面积为 .11. 如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为 cm,侧面积为 ,则这个扇形的圆心角的度数是度. 12. 如图,方老师用一张半径为18cm的扇形纸板,做了一个圆锥形帽子(接缝忽略不计).如果圆锥形帽子的半径是10cm,那么这张扇形纸板的面积是 cm2(结果用含π的式子表示).
12. 如图,方老师用一张半径为18cm的扇形纸板,做了一个圆锥形帽子(接缝忽略不计).如果圆锥形帽子的半径是10cm,那么这张扇形纸板的面积是 cm2(结果用含π的式子表示).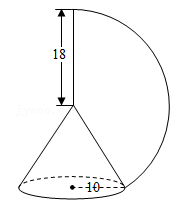 13. 如图,圆锥的高是4,它的侧面展开图是圆心角为120°的扇形,则圆锥的侧面积是.(结果保留 )
13. 如图,圆锥的高是4,它的侧面展开图是圆心角为120°的扇形,则圆锥的侧面积是.(结果保留 )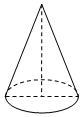 14. 如图所示的扇形中,已知 ,则 .
14. 如图所示的扇形中,已知 ,则 . 15. 如图所示的网格中,每个小正方形的边长均为 ,点 , , 均在小正方形的顶点上,且点 , 在 上, ,则 的长为.
15. 如图所示的网格中,每个小正方形的边长均为 ,点 , , 均在小正方形的顶点上,且点 , 在 上, ,则 的长为.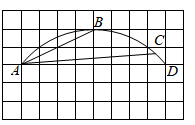 16. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(即阴影部分)面积之和是cm2
16. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(即阴影部分)面积之和是cm2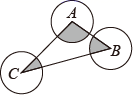
三、解答题
-
17. 一个圆锥的母线长为 底面半径为 ,求这个圆锥的侧面积和全面积.18. 已知半径为6的扇形面积为 ,求此扇形圆心角的角度.19. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,扇形的圆心角 ,求该圆锥的母线长 .

四、综合题
-
20. 某灯具厂生产一批台灯罩,如图的阴影部分为灯罩的侧面展开图.已知半径 , , .(计算结果保留 )
 (1)、若要在灯罩的上下边缘镶上花边(花边的宽度忽略不计),至少需要多长的花边?(2)、求灯罩的侧面积(接缝处忽略不计).21. 已知,如图,扇形AOB的圆心角为120°,半径OA为6cm.
(1)、若要在灯罩的上下边缘镶上花边(花边的宽度忽略不计),至少需要多长的花边?(2)、求灯罩的侧面积(接缝处忽略不计).21. 已知,如图,扇形AOB的圆心角为120°,半径OA为6cm. (1)、求扇形AOB的弧长和扇形面积;(2)、若把扇形纸片AOB卷成一个圆锥无底纸盒,求这个纸盒的高OH.
(1)、求扇形AOB的弧长和扇形面积;(2)、若把扇形纸片AOB卷成一个圆锥无底纸盒,求这个纸盒的高OH.
 ;
; ;
; ;
;

