备考2022年中考数学一轮复习(湘教版)专题49 直线与圆的位置关系
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
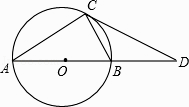
1. 如图,AB是 的直径,BC是 的切线,若 ,则 的大小为( )
 A、 B、 C、 D、2. 如图, 、 分别与 相切于 、 , , 为 上一点,则 的度数为( )
A、 B、 C、 D、2. 如图, 、 分别与 相切于 、 , , 为 上一点,则 的度数为( )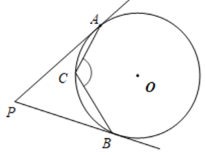 A、 B、 C、 D、3. 若⊙O半径是2,点A在直线l上,且OA=2,则直线l与⊙O的位置关系是( )A、相切 B、相交 C、相离 D、相切或相交4. 如图,AB是⊙O的弦,作OC⊥OA交⊙O的切线BC于点C , 交AB于点D . 已知∠OAB=20°,则∠OCB的度数为( )
A、 B、 C、 D、3. 若⊙O半径是2,点A在直线l上,且OA=2,则直线l与⊙O的位置关系是( )A、相切 B、相交 C、相离 D、相切或相交4. 如图,AB是⊙O的弦,作OC⊥OA交⊙O的切线BC于点C , 交AB于点D . 已知∠OAB=20°,则∠OCB的度数为( ) A、20° B、30° C、40° D、50°5. 如图,在 中,AB是直径,AC是弦,过点C的切线与AB的延长线交于点D,若 ,则 的大小为
A、20° B、30° C、40° D、50°5. 如图,在 中,AB是直径,AC是弦,过点C的切线与AB的延长线交于点D,若 ,则 的大小为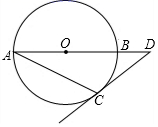 A、 B、 C、 D、6. 如图,在△ABC中,∠A=50°,内切圆I与边BC、CA、AB分别相切于点D、E、F,则∠EDF的度数为( )
A、 B、 C、 D、6. 如图,在△ABC中,∠A=50°,内切圆I与边BC、CA、AB分别相切于点D、E、F,则∠EDF的度数为( )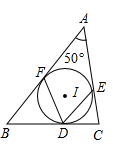 A、55° B、60° C、65° D、70°
A、55° B、60° C、65° D、70°二、填空题
-
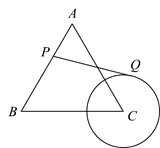
7. 如图,等边三角形ABC的边长为4, 的半径为 ,P为AB边上一动点,过点P作 的切线PQ,切点为Q,则PQ的最小值为.
 8. 如图, 是 的切线, 是切点.若 ,则 .
8. 如图, 是 的切线, 是切点.若 ,则 .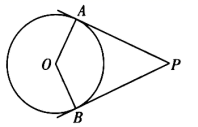 9. 已知△ABC中,⊙I为△ABC的内切圆,切点为H,若BC=6,AC=8,AB=10,则点A到圆上的最近距离等于 .
9. 已知△ABC中,⊙I为△ABC的内切圆,切点为H,若BC=6,AC=8,AB=10,则点A到圆上的最近距离等于 .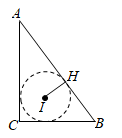 10. 如图,在圆内接四边形ABCD中, 、 、 的度数之比为 ,则 .
10. 如图,在圆内接四边形ABCD中, 、 、 的度数之比为 ,则 . 11. 如图, , 是 的切线,B , C为切点, 是 的直径,延长 交 的延长线于点D,连接 .若 ,则 的度数为 .
11. 如图, , 是 的切线,B , C为切点, 是 的直径,延长 交 的延长线于点D,连接 .若 ,则 的度数为 . 12. 如图,⊙O是等边△ABC的内切圆,分别切AB , BC , AC于点E , F , D , P是 上一点,则∠EPF的度数是 .
12. 如图,⊙O是等边△ABC的内切圆,分别切AB , BC , AC于点E , F , D , P是 上一点,则∠EPF的度数是 .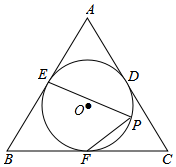
三、作图题
-
13. 已知在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,以AD为弦作⊙O,使圆心O在AB上.
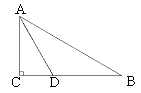 (1)、用直尺和圆规在图中作出⊙O(不写作法,保留作图痕迹) ;(2)、求证:BC为⊙O的切线.14. 画出△ABC的三条角平分线.
(1)、用直尺和圆规在图中作出⊙O(不写作法,保留作图痕迹) ;(2)、求证:BC为⊙O的切线.14. 画出△ABC的三条角平分线. 15.
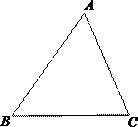
15.如图,有一块三角形材料(△ABC),请你画出一个圆,使其与△ABC的各边都相切.
.
 16.
16.用圆规、直尺作图,不写作法,但要保留作图痕迹.
已知:如图,△ABC是一块等腰三角形的余料,王师傅要在该余料上面截出一块面积最大的半圆形桌面,请你用尺规作图的方法画出这块半圆形桌面。(在题目的原图中完成作图) 17. 如图,点P是⊙O上一点,请用尺规过点P作⊙O的切线(不写画法,保留作图痕迹).
17. 如图,点P是⊙O上一点,请用尺规过点P作⊙O的切线(不写画法,保留作图痕迹).
四、解答题
-
18. 已知:如图,在△OAB中,OA=OB,⊙O与AB相切于点C。求证:AC=BC。
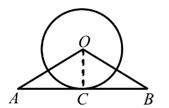
小明同学的证明过程如下框:
证明:连结OC
∵OA=OB,∴∠A=∠B
又∵OC=OC,
∴△OAC≌OBC,
∴AC=BC
小明的证法是否正确?若正确,请在框内打“√”;若错误,请写出你的证明过程。
19.如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
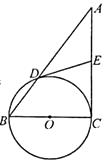 (1)、求证:∠A=∠ADE;(2)、若AD=16,DE=10,求BC的长.20. 如图,AM切⊙O于点A,BD⊥AM于点D,BD交⊙O于点C,OC平分∠AOB.求∠B的度数.
(1)、求证:∠A=∠ADE;(2)、若AD=16,DE=10,求BC的长.20. 如图,AM切⊙O于点A,BD⊥AM于点D,BD交⊙O于点C,OC平分∠AOB.求∠B的度数. 21. 如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=2∠B,⊙O的切线AP与OC的延长线相交于点P,若PA= cm,求AC的长.
21. 如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=2∠B,⊙O的切线AP与OC的延长线相交于点P,若PA= cm,求AC的长. 22. 如图,AB,CD是⊙O的直径,点E在AB延长线上,FE⊥AB,BE=EF=2,FE的延长线交CD延长线于点G,DG=GE=3,连接FD.
22. 如图,AB,CD是⊙O的直径,点E在AB延长线上,FE⊥AB,BE=EF=2,FE的延长线交CD延长线于点G,DG=GE=3,连接FD.(1)求⊙O的半径;
(2)求证:DF是⊙O的切线.

五、综合题
-
23. 我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”,三斜即指三角形的三条边长,可以用该方法求三角形面积.若改用现代数学语言表示,其形式为:设 , , 为三角形三边, 为面积,则 ①
这是中国古代数学的瑰宝之一.
而在文明古国古希腊,也有一个数学家海伦给出了求三角形面积的另一个公式,若设 (周长的一半),则 ②
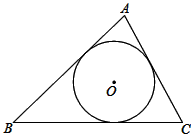 (1)、尝试验证.这两个公式在表面上形式很不一致,请你用以5,7,8为三边构成的三角形,分别验证它们的面积值;(2)、问题探究.经过验证,你发现公式①和②等价吗?若等价,请给出一个一般性推导过程(可以从① ②或者② ① ;(3)、问题引申.三角形的面积是数学中非常重要的一个几何度量值,很多数学家给出了不同形式的计算公式.请你证明如下这个公式:如图, 的内切圆半径为 ,三角形三边长为 , , ,仍记 , 为三角形面积,则 .24. 如图, 是 的直径, 是 上一点,过点 作 ,交 的延长线于 ,交 于点 , 是 的中点,连接 .
(1)、尝试验证.这两个公式在表面上形式很不一致,请你用以5,7,8为三边构成的三角形,分别验证它们的面积值;(2)、问题探究.经过验证,你发现公式①和②等价吗?若等价,请给出一个一般性推导过程(可以从① ②或者② ① ;(3)、问题引申.三角形的面积是数学中非常重要的一个几何度量值,很多数学家给出了不同形式的计算公式.请你证明如下这个公式:如图, 的内切圆半径为 ,三角形三边长为 , , ,仍记 , 为三角形面积,则 .24. 如图, 是 的直径, 是 上一点,过点 作 ,交 的延长线于 ,交 于点 , 是 的中点,连接 .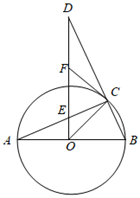 (1)、求证: 是 的切线.(2)、若 ,求证: .25. 如图, ,点 、 分别在射线 、 上, , .
(1)、求证: 是 的切线.(2)、若 ,求证: .25. 如图, ,点 、 分别在射线 、 上, , .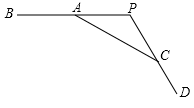 (1)、用尺规在图中作一段劣弧,使得它在 、 两点分别与射线 和 相切.要求:写出作法,并保留作图痕迹;(2)、根据(1)的作法,结合已有条件,请写出已知和求证,并证明;(3)、求所得的劣弧与线段 、 围成的封闭图形的面积.
(1)、用尺规在图中作一段劣弧,使得它在 、 两点分别与射线 和 相切.要求:写出作法,并保留作图痕迹;(2)、根据(1)的作法,结合已有条件,请写出已知和求证,并证明;(3)、求所得的劣弧与线段 、 围成的封闭图形的面积.