备考2022年中考数学一轮复习（湘教版）专题48 垂径定理

试卷更新日期：2021-09-22 类型：一轮复习

进入出卷网下载

一、单选题

1. 学习圆的性质后，小铭与小熹就讨论起来，小铭说：“被直径平分的弦也与直径垂直”，小熹说：“用反例就能说明这是假命题” .下列判断正确的是（）

A、两人说的都对 B、小铭说的对，小燕说的反例不存在 C、两人说的都不对 D、小铭说的不对，小熹说的反例存在

查看试题解析
2. 如图是一位同学从照片上剪切下来的海上日出时的画面，“图上”太阳与海平线交于 $A$ ， $B$ 两点，他测得“图上”圆的半径为10厘米， $A B = 16$ 厘米．若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟，则“图上”太阳升起的速度为（）．

A、1.0厘米/分 B、0.8厘米分 C、12厘米/分 D、1.4厘米/分

查看试题解析
3. 如图，AB为圆O的直径，C、D两点均在圆上，其中OD⊥AC交AC于E点．若DE＝1，BC＝6，则AC＝（）

A、3 B、 $2 \sqrt{6}$ C、5 D、 $2 \sqrt{7}$

查看试题解析
4. 如图，是某供水管道的截面图，里面尚有一些水，若液面宽度AB＝8cm，半径OC⊥AB于D ，液面深度CD＝2cm，则该管道的半径长为（）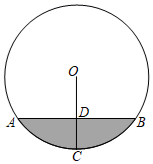

A、6cm B、5.5cm C、5cm D、4cm

查看试题解析
5. 已知⊙O的直径CD＝100cm，AB是⊙O的弦，AB⊥CD，垂足为M，且AB＝96cm，则AC的长为（）

A、36cm或64cm B、60cm或80cm C、80cm D、60cm

查看试题解析
6. AB和CD是⊙O的两条平行弦，AB＝6，CD＝8，⊙O的半径为5，则AB与CD间的距离为（）

A、1或7 B、7 C、1 D、3或4

查看试题解析

二、填空题

7. 如图，在⊙O中，弦 $A B$ 的长为4，圆心 $O$ 到弦 $A B$ 的距离为2，则 $∠ A O C$ 的度数为.

查看试题解析
8. 一根横截面为圆形的下水管的直径为1米，管内污水的水面宽为0.8米，那么管内污水深度为米．

查看试题解析
9. 如图，已知⊙O半径为5，弦AB长为8，点P为弦AB上一动点，连结OP，则线段OP的最小长度是.

查看试题解析
10. 如图，在平面直角坐标系中，一个圆经过 $O (0 ， 0)$ ， $A (3 ， 5)$ ， $B (6 ， 0)$ 三点，则该圆的圆心的坐标是.

查看试题解析
11. 已知在半径为3的 $⊙ O$ 中，弦 $A B$ 的长为4，那么圆心 $O$ 到 $A B$ 的距离为.

查看试题解析
12. 一个圆柱体容器内装入一些水，截面如图所示，若⊙O中的直径为52cm，水面宽AB＝48cm，则水的最大深度为cm．

查看试题解析

三、解答题

13. 如图1，点 $P$ 表示我国古代水车的一个盛水筒.如图2，当水车工作时，盛水筒的运行路径是以轴心 $O$ 为圆心， $5 m$ 为半径的圆.若 $⊙ O$ 被水面截得的弦 $A B$ 长为 $8 m$ ，求水车工作时，盛水筒在水面以下的最大深度.

查看试题解析
14. 如图AB是⊙O的直径，弦CD⊥AB于点E，若EB＝9，AE＝1，求弦CD的长.

查看试题解析

四、综合题

15. 如图1是一个用铁丝围成的篮框，我们来仿制一个类似的柱体形篮框．如图2，它是由一个半径为r、圆心角90°的扇形A₂OB₂ ，矩形A₂C₂EO、B₂D₂EO，及若干个缺一边的矩形状框A₁C₁D₁B₁、A₂C₂D₂B₂、…、A_nB_nC_nD_n ， OEFG围成，其中A₁、G、B₁在 $\hat{A_{2} B_{2}}$ 上，A₂、A₃…、A_n与B₂、B₃、…B_n分别在半径OA₂和OB₂上，C₂、C₃、…、C_n和D₂、D₃…D_n分别在EC₂和ED₂上，EF⊥C₂D₂于H₂ ， C₁D₁⊥EF于H₁ ， FH₁=H₁H₂=d，C₁D₁、C₂D₂、C₃D₃、C_nD_n依次等距离平行排放（最后一个矩形状框的边C_nD_n与点E间的距离应不超过d），A₁C₁∥A₂C₂∥A₃C₃∥…∥A_nC_n

(1)、求d的值；

(2)、问：C_nD_n与点E间的距离能否等于d？如果能，求出这样的n的值，如果不能，那么它们之间的距离是多少？

查看试题解析
16. 一次函数 $y = k x + b$ 的图象与轴的负半轴相交于点 $A$ ，与 $y$ 轴的正半轴相交于点 $B$ ，且 $\sin ∠ A B O = \frac{\sqrt{3}}{2}$ ． $Δ O A B$ 的外接圆的圆心 $M$ 的横坐标为 $- 3$ ．

(1)、求一次函数的解析式；

(2)、求图中阴影部分的面积．

查看试题解析
17. 如图，在圆O中，弦AB＝8，点C在圆O上（C与A ， B不重合），连接CA、CB ，过点O分别作OD⊥AC ， OE⊥BC ，垂足分别是点D、E ．

(1)、求线段DE的长；

(2)、点O到AB的距离为3，求圆O的半径．

查看试题解析