备考2022年中考数学一轮复习(湘教版)专题47 圆心角、 圆周角
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
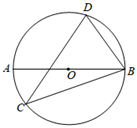
1. 如图,AB为 的直径,C , D为 上的两点,若 ,则 的度数为( )
 A、 B、 C、 D、2. 如图,A , B , C是⊙O上的三点,若 ,则 的度数是( )
A、 B、 C、 D、2. 如图,A , B , C是⊙O上的三点,若 ,则 的度数是( ) A、40° B、35° C、30° D、25°3. 如图,点A , B , C为⊙O上的三点,∠AOB ∠BOC , ∠BAC=30°,则∠AOC的度数为( )
A、40° B、35° C、30° D、25°3. 如图,点A , B , C为⊙O上的三点,∠AOB ∠BOC , ∠BAC=30°,则∠AOC的度数为( )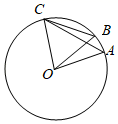 A、100° B、90° C、80° D、60°4. 如图,四边形 内接于 ,点 为边 上任意一点(点 不与点 , 重合)连接 .若 ,则 的度数可能为( )
A、100° B、90° C、80° D、60°4. 如图,四边形 内接于 ,点 为边 上任意一点(点 不与点 , 重合)连接 .若 ,则 的度数可能为( )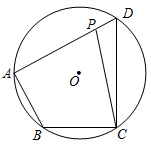 A、 B、 C、 D、5. 如图,A,B,C是半径为1的⊙O上的三个点,若AB= ,∠CAB=30°,则∠ABC的度数为( )
A、 B、 C、 D、5. 如图,A,B,C是半径为1的⊙O上的三个点,若AB= ,∠CAB=30°,则∠ABC的度数为( ) A、95° B、100° C、105° D、110°6. 如图, , 是 上直径 两侧的两点.设 ,则 ( )
A、95° B、100° C、105° D、110°6. 如图, , 是 上直径 两侧的两点.设 ,则 ( ) A、 B、 C、 D、7. 如图,点 , , 是 上的三点.若 , ,则 的大小为( )
A、 B、 C、 D、7. 如图,点 , , 是 上的三点.若 , ,则 的大小为( )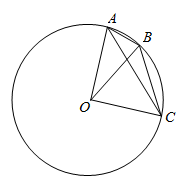 A、 B、 C、 D、8. 如图, 是 直径,点C、D将 分成相等的三段弧,点P在 上.已知点Q在 上且 ,则点Q所在的弧是( )
A、 B、 C、 D、8. 如图, 是 直径,点C、D将 分成相等的三段弧,点P在 上.已知点Q在 上且 ,则点Q所在的弧是( )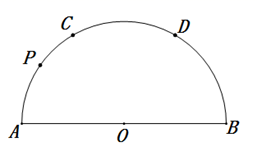 A、 B、 C、 D、9. 如图,点A , B , C , D四点均在⊙O上,∠AOD=68°,AO∥DC , 则∠B的度数为( )
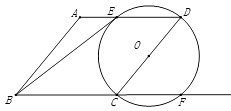
A、 B、 C、 D、9. 如图,点A , B , C , D四点均在⊙O上,∠AOD=68°,AO∥DC , 则∠B的度数为( ) A、40° B、60° C、56° D、68°10. 如图, 的弦CD与直径AB的延长线相交于点E, , ,则 ( )
A、40° B、60° C、56° D、68°10. 如图, 的弦CD与直径AB的延长线相交于点E, , ,则 ( )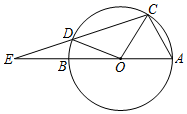 A、60° B、72° C、75° D、78°
A、60° B、72° C、75° D、78°二、填空题
-
11. 已知⊙O的半径是7,AB是⊙O的弦,且AB的长为7 ,则弦AB所对的圆周角的度数为 .12. 点 是 的外心,若 ,则 为.13. 如图, 是 的直径,点 在 上,若 ,则 °.
 14. 如图, 是 的外接圆,连接 并延长交 于点 ,若 ,则 的度数为.
14. 如图, 是 的外接圆,连接 并延长交 于点 ,若 ,则 的度数为.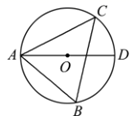 15. 如图,四边形ABCD内接于⊙O,连接BD,若 = ,∠BDC=50°,则∠ADC=度
15. 如图,四边形ABCD内接于⊙O,连接BD,若 = ,∠BDC=50°,则∠ADC=度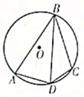 16. 如图,O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=38º,则∠OAC的度数是.
16. 如图,O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=38º,则∠OAC的度数是.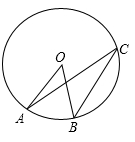 17. 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第23秒时,点E在量角器上对应的度数是度.
17. 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第23秒时,点E在量角器上对应的度数是度.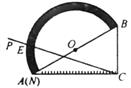 18. 如图,已知在△ABC中,AB=AC.以AB为直径作半圆O,交BC于点D.若∠BAC=40°,则的度数是度.
18. 如图,已知在△ABC中,AB=AC.以AB为直径作半圆O,交BC于点D.若∠BAC=40°,则的度数是度.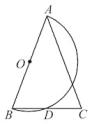 19. 已知弦AB把圆周分成1:5的两部分,则弦AB所对的圆心角的度数为度。
19. 已知弦AB把圆周分成1:5的两部分,则弦AB所对的圆心角的度数为度。三、解答题
-
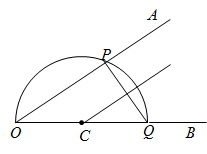
20. 如下是小华设计的“作 的角平分线”的尺规作图过程,请帮助小华完成尺规作图并填空(保留作图痕迹).
步骤
作法
推断
第一步
在 上任取一点C , 以点C为圆心, 为半径作半圆,分别交射线 于点P , 点Q , 连接
▲ ,理由是 ▲
第二步
过点C作 的垂线,交 于点D , 交 于点E
, ③
第三步
作射线
射线 平分
射线 为所求作.
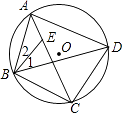
21. 如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD.求证:CE=BE.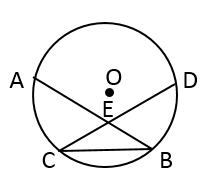 22. 如图,⊙O是△ABC的外接圆,∠AOB=96°,∠CAB=60°,点D是 的中点.求∠ABD的度数.
22. 如图,⊙O是△ABC的外接圆,∠AOB=96°,∠CAB=60°,点D是 的中点.求∠ABD的度数.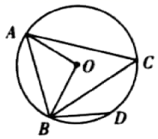 23. 如图,A、B、C在⊙O上,若 ,求证: .
23. 如图,A、B、C在⊙O上,若 ,求证: .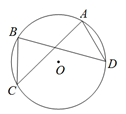 24. 如图,在⊙O中, ,CD⊥OA于D , CE⊥OB于E.求证:AD=BE.
24. 如图,在⊙O中, ,CD⊥OA于D , CE⊥OB于E.求证:AD=BE.
四、综合题
-
25. 已知:如图,点M为锐角∠APB的边PA上一点.
求作:∠AMD,使得点D在边PB上,且∠AMD =2∠P.
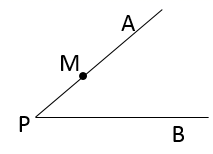
作法:①以点M为圆心,MP长为半径画圆,交PA于另一点C,交PB 于点D点;
②作射线MD.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:∵P、C、D都在⊙M上,
∠P为弧CD所对的圆周角,∠CMD为弧CD所对的圆心角,
∴∠P= ∠CMD()(填推理依据).
∴∠AMD =2∠P.
26. 如图, 是 上的5等分点,连接 ,得到一个五角星图形和五边形 . (1)、计算 的度数;(2)、连接 ,证明: ;(3)、求证: .
(1)、计算 的度数;(2)、连接 ,证明: ;(3)、求证: .