备考2022年中考数学一轮复习(湘教版)专题46 圆及其对称性
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
1. 如图,已知长方形 中, ,圆B的半径为1,圆A与圆B内切,则点 与圆A的位置关系是( )
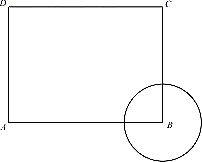 A、点C在圆A外,点D在圆A内 B、点C在圆A外,点D在圆A外 C、点C在圆A上,点D在圆A内 D、点C在圆A内,点D在圆A外2. 的半径为 点 到圆心 的距离为 则点 与 的位置关系是( )A、在圆上 B、在圆内 C、在圆外 D、不确定3. 如图,在平面直角坐标系xOy中,点A为(0,3),点B为(2,1),点C为(2,-3).则经画图操作可知:△ABC的外心坐标应是( )
A、点C在圆A外,点D在圆A内 B、点C在圆A外,点D在圆A外 C、点C在圆A上,点D在圆A内 D、点C在圆A内,点D在圆A外2. 的半径为 点 到圆心 的距离为 则点 与 的位置关系是( )A、在圆上 B、在圆内 C、在圆外 D、不确定3. 如图,在平面直角坐标系xOy中,点A为(0,3),点B为(2,1),点C为(2,-3).则经画图操作可知:△ABC的外心坐标应是( ) A、 B、 C、 D、4. 为准备一次大型实景演出,某旅游区划定了边长为 的正方形演出区域,并在该区域画出4×4的网格以便演员定位(如图所示),其中 为中心, , , , 是某节目中演员的四个定位点.为增强演出效果,总策划决定在该节目演出过程中增开人工喷泉.喷头位于演出区域东侧,且在中轴线 上与点 相距 处.该喷泉喷出的水流落地半径最大为 ,为避免演员被喷泉淋湿,需要调整的定位点的个数是( )
A、 B、 C、 D、4. 为准备一次大型实景演出,某旅游区划定了边长为 的正方形演出区域,并在该区域画出4×4的网格以便演员定位(如图所示),其中 为中心, , , , 是某节目中演员的四个定位点.为增强演出效果,总策划决定在该节目演出过程中增开人工喷泉.喷头位于演出区域东侧,且在中轴线 上与点 相距 处.该喷泉喷出的水流落地半径最大为 ,为避免演员被喷泉淋湿,需要调整的定位点的个数是( ) A、1个 B、2个 C、3个 D、4个5. 的半径为3,点 在 外,点 到圆心的距离为 ,则 需要满足的条件( )A、 B、 C、 D、无法确定6. 下列说法错误的是( )A、已知圆心和半径可以作一个圆 B、经过一个已知点A的圆能做无数个 C、经过两个已知点A , B的圆能做两个 D、经过不在同一直线上的三个点A , B , C只能做一个圆7. 过钝角三角形的三个顶点作圆,其圆心在( )A、三角形内 B、三角形上 C、三角形外 D、以上都有可能8. 如图,在矩形ABCD中,AB=6,AD=8,若以点A为圆心,8为半径作⊙A , 则下列各点在⊙A外的是( )
A、1个 B、2个 C、3个 D、4个5. 的半径为3,点 在 外,点 到圆心的距离为 ,则 需要满足的条件( )A、 B、 C、 D、无法确定6. 下列说法错误的是( )A、已知圆心和半径可以作一个圆 B、经过一个已知点A的圆能做无数个 C、经过两个已知点A , B的圆能做两个 D、经过不在同一直线上的三个点A , B , C只能做一个圆7. 过钝角三角形的三个顶点作圆,其圆心在( )A、三角形内 B、三角形上 C、三角形外 D、以上都有可能8. 如图,在矩形ABCD中,AB=6,AD=8,若以点A为圆心,8为半径作⊙A , 则下列各点在⊙A外的是( ) A、点A B、点B C、点C D、点D9. 在平面直角坐标系 中,⊙O的半径为2,点A(1, )与⊙O的位置关系是( )A、在⊙O上 B、在⊙O内 C、在⊙O外 D、不能确定10. 在如图所示的正方形网格中,点A,B,C,D,O均在格点上,则点O是( )
A、点A B、点B C、点C D、点D9. 在平面直角坐标系 中,⊙O的半径为2,点A(1, )与⊙O的位置关系是( )A、在⊙O上 B、在⊙O内 C、在⊙O外 D、不能确定10. 在如图所示的正方形网格中,点A,B,C,D,O均在格点上,则点O是( )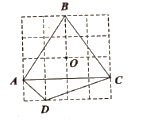 A、 的外心 B、 的内心 C、 的外心 D、 的内心
A、 的外心 B、 的内心 C、 的外心 D、 的内心二、填空题
-
11. 点 是非圆上一点,若点 到 上的点的最小距离是 ,最大距离是 ,则 的半径是 .12. 已知 的半径为 , ,则点P在 的.(填“上面”“内部”或“外部”)13. 如图,在直角坐标系中,点A(0,6)、B(0,﹣2)、C(﹣4,6),则△ABC外接圆的圆心坐标为 .
 14. 如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为.
14. 如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为.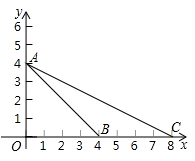 15. 已知圆的直径为13㎝,圆心到直线L的距离为6cm,那么直线L和这个圆的公共点的个数为.16. 已知⊙O的半径是5,点P不在⊙O外,则线段OP的长得取值范围是.17. 若圆 的半径是 ,圆心的坐标是 ,点 的坐标是 ,则点 与 的位置关系是(选填“在圆上”、“在圆外”或“在圆内”)18. 平面上有⊙O及一点P,P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为cm.19. 如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为 .
15. 已知圆的直径为13㎝,圆心到直线L的距离为6cm,那么直线L和这个圆的公共点的个数为.16. 已知⊙O的半径是5,点P不在⊙O外,则线段OP的长得取值范围是.17. 若圆 的半径是 ,圆心的坐标是 ,点 的坐标是 ,则点 与 的位置关系是(选填“在圆上”、“在圆外”或“在圆内”)18. 平面上有⊙O及一点P,P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为cm.19. 如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为 .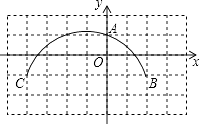 20. 我国魏晋时期数学家刘徽首创“割圆术”计算圆周率.随着时代发展,现在人们依据频率估计概率这一原理,常用随机模拟的方法对圆周率π进行估计,用计算机随机产生m个有序数对(x,y)(x,y是实数,且0≤x≤1,0≤y≤1),它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部.如果统计出这些点中到原点的距离小于或等于1的点有n个,则据此可估计π的值为 . (用含m,n的式子表示)
20. 我国魏晋时期数学家刘徽首创“割圆术”计算圆周率.随着时代发展,现在人们依据频率估计概率这一原理,常用随机模拟的方法对圆周率π进行估计,用计算机随机产生m个有序数对(x,y)(x,y是实数,且0≤x≤1,0≤y≤1),它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部.如果统计出这些点中到原点的距离小于或等于1的点有n个,则据此可估计π的值为 . (用含m,n的式子表示)三、作图题
-
21. 如图,已知△ABC,请用尺规作△ABC的外接圆⊙O.(保留作图痕迹,不写作法)
 22. 已知:在△ABC中,AB=AC。
22. 已知:在△ABC中,AB=AC。 (1)、求作:△ABC的外接圆。(要求:尺规作图,保留作图痕迹,不写作法)(2)、若△ABC的外接圆的圆心O到BC边的距离为4,BC=6,则⊙O的面积=。23. 如图是一名考古学家发现的一块古代车轮碎片,你能帮他找到这个车轮的半径吗?(画出示意图,保留作图痕迹)
(1)、求作:△ABC的外接圆。(要求:尺规作图,保留作图痕迹,不写作法)(2)、若△ABC的外接圆的圆心O到BC边的距离为4,BC=6,则⊙O的面积=。23. 如图是一名考古学家发现的一块古代车轮碎片,你能帮他找到这个车轮的半径吗?(画出示意图,保留作图痕迹) 24. 如图,用尺规作出△ABC的外接圆⊙O,保留作图痕迹,不写作法.
24. 如图,用尺规作出△ABC的外接圆⊙O,保留作图痕迹,不写作法.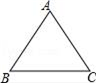 25. 如图,已知 中, ,请作 的外接圆 保面作图痕迹,不写作法
25. 如图,已知 中, ,请作 的外接圆 保面作图痕迹,不写作法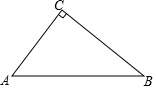
四、解答题
-
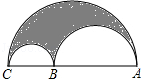
26. 如图,点B是线段AC上的一点,分别以AB、BC、CA为直径作半圆,求证:半圆AB的长与半圆BC的长之和等于半圆AC的长.
 27. 已知:如图,△ABC中, , cm, cm,CM是中线,以C为圆心,以 cm长为半径画圆,则点A、B、M与⊙C的关系如何?
27. 已知:如图,△ABC中, , cm, cm,CM是中线,以C为圆心,以 cm长为半径画圆,则点A、B、M与⊙C的关系如何?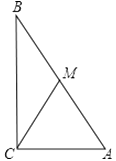 28. 如图,AB、AC是⊙O的两条弦,且AB=AC.求证:∠1=∠2.
28. 如图,AB、AC是⊙O的两条弦,且AB=AC.求证:∠1=∠2. 29. 在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,以r=3为半径作圆,判断A,B两点和⊙C的位置关系.30. 如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,求线段OM的最小值.
29. 在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,以r=3为半径作圆,判断A,B两点和⊙C的位置关系.30. 如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,求线段OM的最小值.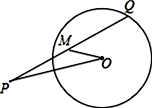
五、综合题
-
31. 如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,
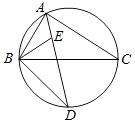 (1)、求证:DE=DB;(2)、若∠BAC=90°,BD=4,求△ABC外接圆的半径.32. 如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)、求证:DE=DB;(2)、若∠BAC=90°,BD=4,求△ABC外接圆的半径.32. 如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.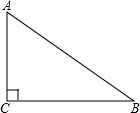 (1)、当r取什么值时,点A、B在⊙C外(2)、当r在什么范围时,点A在⊙C内,点B在⊙C外.33. 如图,在直角梯形ABCD中,AD∥BC, , ,M为AB的中点,以CD为直径画圆P.
(1)、当r取什么值时,点A、B在⊙C外(2)、当r在什么范围时,点A在⊙C内,点B在⊙C外.33. 如图,在直角梯形ABCD中,AD∥BC, , ,M为AB的中点,以CD为直径画圆P. (1)、当点M在圆P外时,求CD的长的取值范围;(2)、当点M在圆P上时,求CD的长;(3)、当点M在圆P内时,求CD的长的取值范围.34. 如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.
(1)、当点M在圆P外时,求CD的长的取值范围;(2)、当点M在圆P上时,求CD的长;(3)、当点M在圆P内时,求CD的长的取值范围.34. 如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.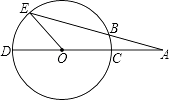 (1)、求∠AOB的度数.(2)、求∠EOD的度数.35. 如图,已知△ABC中,∠C=90°,AC=3,BC=4,已点C为圆心作⊙C,半径为r.
(1)、求∠AOB的度数.(2)、求∠EOD的度数.35. 如图,已知△ABC中,∠C=90°,AC=3,BC=4,已点C为圆心作⊙C,半径为r. (1)、当r取什么值时,点A、B在⊙C外?(2)、当r取什么值时,点A在⊙C内,点B在⊙C外.36. 阅读下列材料,并完成相应的学习任务:
(1)、当r取什么值时,点A、B在⊙C外?(2)、当r取什么值时,点A在⊙C内,点B在⊙C外.36. 阅读下列材料,并完成相应的学习任务:我们知道三角形外接圆的圆心叫做三角形的外心,三角形内切圆的圆心叫做三角形的内心.由于三角形的三条高(或高所在的直线)相交于一点,因此我们把三角形三条高的交点叫做三角形的垂心.下面我们以锐角三角形为例,证明三角形的三条高相交于一点.
如图,在△ABC中,AD , BE分别是BC , AC边上的高,且AD与BE相交于点P . 连接CP并延长,交AB于点F .
求证:CF⊥AB .
证明:分别过点A , B , C作它们所对边的平行线,三条平行线两两相交于点M , N , Q . 分别连接PM , PN , PQ .
∵MN BC , MQ AB , NQ AC ,
∴四边形MABC , 四边形ANBC , 四边形ABQC都是平行四边形.
∴BC=AM=AN , AC=BN=BQ , AB=MC=CQ .
∵AD⊥BC ,
∴∠MAD=∠ADB=90°,即AD⊥MN .
∴PM=PN .
…
学习任务:
(1)、请将上面剩余的证明过程补充完整;(2)、点P是△MNQ的 . (填出字母代号即可)A、内心 B、外心 C、垂心 D、重心(3)、若∠CAB=40°,则∠MPN=°.