备考2022年中考数学一轮复习（湘教版）专题43 多边形
试卷更新日期：2021-09-22 类型：一轮复习
一、单选题
-
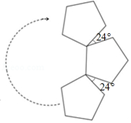
1. 正多边形的一个外角等于60°，这个多边形的边数是（ ）A、3 B、6 C、9 D、122. 一个多边形的内角和是1800°，则这个多边形是（ ）边形.A、9 B、10 C、11 D、123. 一个十边形的内角和等于（ ）A、 B、 C、 D、4. 若一个正 边形的每个内角为150°，则这个正 边形的边数是（ ）A、10 B、11 C、12 D、135. 如图，用若n个全等的正五边形按如下方式拼接可以拼成一个环状，使相邻的两个正五边形有公共顶点，所夹的锐角为24°，图中所示的是前3个正五边形的拼接情况，拼接一圈后，中间会形成一个正多边形，则n的值为（ ）
A、5 B、6 C、8 D、106. 若一个多边形的内角和是540°，则该多边形的边数为（ ）A、4 B、5 C、6 D、7二、填空题
-
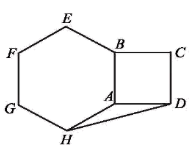
7. 一个多边形的每一个外角都等于60°，则这个多边形的内角和为 度.8. 正五边形的一个外角的大小为度．9. 正六边形的一个内角是正n边形一个外角的4倍，则n= ．10. 若一个多边形的内角和等于外角和，那么这个多边形的边数是 ．11. 八边形的内角和为度．12. 如图，以正方形ABCD的AB边向外作正六边形ABEFGH，连接DH，则∠ADH=°
三、作图题
-
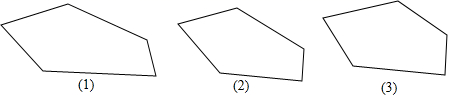
13. 如图是一个多边形，你能否用一直线去截这个多边形，使得到的新多边形分别满足下列条件： 画出图形，把截去的部分打上阴影
(1)、①新多边形内角和比原多边形的内角和增加了 ．②新多边形的内角和与原多边形的内角和相等．
③新多边形的内角和比原多边形的内角和减少了 ．
(2)、将多边形只截去一个角，截后形成的多边形的内角和为 ，求原多边形的边数．14. 画出如图多边形的全部对角线．
15.画出下列多边形的全部对角线．
16.画出下面多边形的全部对角线．
四、解答题
-
17. 在凸多边形中, 四边形有2条对角线, 五边形有5条对角线, 经过观察、探索、归纳, 你认为凸八边形的对角线条数应该是多少条? 简单扼要地写出你的思考过程.18. 一个多边形的内角和与外角和的度数之和为 ，求这个多边形的边数．19. 某科技小组制作了一个机器人，它能根据指令要求进行行进和旋转，某一指令规定：机器人先向前方行走2 m，然后左转60°，若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了多少米?20. 如果多边形的每个内角都比它相邻的外角的4倍还多 ，求这个多边形的内角和.
五、综合题
-
21. 已知n边形的内角和θ=（n-2）×180°.(1)、甲同学说，θ能取360°；而乙同学说，θ也能取630°.甲、乙的说法对吗？若对，求出边数n.若不对，说明理由；(2)、若n边形变为（n+x）边形，发现内角和增加了360°，用列方程的方法确定x.22. 连接多边形任意两个不相邻顶点的线段称为多边形的对角线.
(1)、
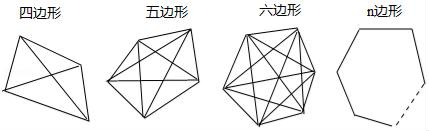
对角线条数分别为、、、.
(2)、n边形可以有20条对角线吗？如果可以，求边数n的值；如果不可以，请说明理由.(3)、若一个n边形的内角和为1800°，求它对角线的条数．
23. 在一个多边形中，一个内角相邻的外角与其他各内角的和为600°．(1)、如果这个多边形是五边形，请求出这个外角的度数；(2)、是否存在符合题意的其他多边形？如果存在，请求出边数及这个外角的度数；如果不存在，请说明理由．
