备考2022年中考数学一轮复习(湘教版)专题42 角平分线
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
1. 如图,在 中, , , ,BD平分 ,则点D到AB的距离等于( )
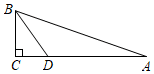 A、4 B、3 C、2 D、12. 如图,AM为∠BAC的平分线,下列等式错误的是( )
A、4 B、3 C、2 D、12. 如图,AM为∠BAC的平分线,下列等式错误的是( )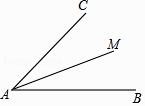 A、∠BAC=∠BAM B、∠BAM=∠CAM C、∠BAM=2∠CAM D、2∠CAM=∠BAC3. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A、∠BAC=∠BAM B、∠BAM=∠CAM C、∠BAM=2∠CAM D、2∠CAM=∠BAC3. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )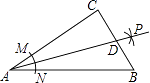 A、15 B、30 C、45 D、604. 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是( )
A、15 B、30 C、45 D、604. 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是( ) A、PC=PD B、∠CPD=∠DOP C、∠CPO=∠DPO D、OC=OD5. 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A、PC=PD B、∠CPD=∠DOP C、∠CPO=∠DPO D、OC=OD5. 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( ) A、8 B、6 C、4 D、26. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A、8 B、6 C、4 D、26. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( ) A、15 B、30 C、45 D、607.
A、15 B、30 C、45 D、607.观察图中尺规作图痕迹,下列结论错误的是( )
 A、PQ为∠APB的平分线 B、PA=PB C、点A、B到PQ的距离不相等 D、∠APQ=∠BPQ8.
A、PQ为∠APB的平分线 B、PA=PB C、点A、B到PQ的距离不相等 D、∠APQ=∠BPQ8.如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于( )
 A、35° B、70° C、110° D、145°
A、35° B、70° C、110° D、145°二、填空题
-
9. 在x轴,y轴上分别截取 ,再分别以点A,B为圆心,以大于 长为半径画弧,两弧交于点P,若点P的坐标为 ,则a的值是.10. 如图, 是 的角平分线.若 ,则点D到 的距离是.
 11. 如图,在Rt△ABC中,∠B=90°,以顶点C为圆心,适当长为半径画弧,分别交AC,BC于点E,F,再分别以点E,F为圆心,大于 EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D.若BD=3,AC=10,则△ACD的面积是 .
11. 如图,在Rt△ABC中,∠B=90°,以顶点C为圆心,适当长为半径画弧,分别交AC,BC于点E,F,再分别以点E,F为圆心,大于 EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D.若BD=3,AC=10,则△ACD的面积是 .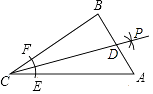 12. 如图所示,已知∠AOB=40°,现按照以下步骤作图:
12. 如图所示,已知∠AOB=40°,现按照以下步骤作图: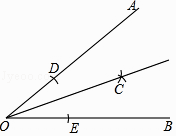
①在OA,OB上分别截取线段OD,OE,使OD=OE;
②分别以D,E为圆心,以大于 DE的长为半径画弧,在∠AOB内两弧交于点C;
③作射线OC.
则∠AOC的大小为 .
13. 如图,△ABC中,∠C=90°,∠BAC的平分线交BC于点D,若CD=4,则点D到AB的距离是 .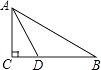 14. 如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 .
14. 如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 . 15. 在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=4,则点D到斜边AB的距离为 .
15. 在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=4,则点D到斜边AB的距离为 .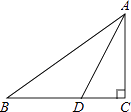 16. 如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是 .
16. 如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是 .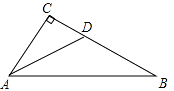 17.
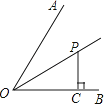
17.如图,OP为∠AOB的平分线,PC⊥OB于点C,且PC=3,点P到OA的距离为 .
三、作图题
-
18. 如图,有一块三角形材料(△ABC),请你在这块材料上作一个面积最大的圆.
 19. 如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心在线段AC上,且与AB、BC都相切.请你用直尺和圆规画出来(要求用尺规作图,保留作图痕迹,不要求写作法).
19. 如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心在线段AC上,且与AB、BC都相切.请你用直尺和圆规画出来(要求用尺规作图,保留作图痕迹,不要求写作法). 20. 如图,已知 ,请用尺规在 中找一点 ,使得点 到 三边的距离相等.(保留作图痕迹,不写作法)
20. 如图,已知 ,请用尺规在 中找一点 ,使得点 到 三边的距离相等.(保留作图痕迹,不写作法) 21. 已知:线段a及∠ACB.
21. 已知:线段a及∠ACB.求作:⊙O,使⊙O在∠ACB的内部,CO=a,且⊙O与∠ACB的两边分别相切.
 22. 如图,工人师傅要利用一块形状为直角三角形(∠C为直角)的铁皮加工一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上.请作出这个正方形零件在AB边上的顶点M.
22. 如图,工人师傅要利用一块形状为直角三角形(∠C为直角)的铁皮加工一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上.请作出这个正方形零件在AB边上的顶点M.
四、解答题
-
23. 如图,已知 平分 , .求证: .
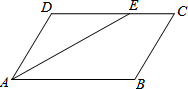
 24. 已知:如图,在▱ABCD中,AE平分∠DAB , 交CD于点E .
24. 已知:如图,在▱ABCD中,AE平分∠DAB , 交CD于点E .求证:DA=DE .
 25. 在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=7.8cm,求点D到AB的距离.
25. 在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=7.8cm,求点D到AB的距离.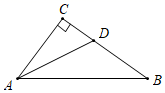 26. 如图,在Rt△ABC中,∠C=90°,∠A= ∠ABC,BD平分∠ABC,DE⊥AB,CD=4cm,求AB的长.
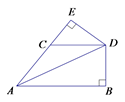
26. 如图,在Rt△ABC中,∠C=90°,∠A= ∠ABC,BD平分∠ABC,DE⊥AB,CD=4cm,求AB的长. 27. 如图,在等腰△ACD中,AC=CD,且CD∥AB,DE⊥AC,交AC延长线于点E,DB⊥AB于B。
27. 如图,在等腰△ACD中,AC=CD,且CD∥AB,DE⊥AC,交AC延长线于点E,DB⊥AB于B。求证:DE=DB.
五、综合题
-
28. 已知:如图,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.
 (1)、求证:AM平分∠DAB.(2)、试说明线段DM与AM有怎样的位置关系?并证明你的结论.29. 如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)、求证:AM平分∠DAB.(2)、试说明线段DM与AM有怎样的位置关系?并证明你的结论.29. 如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF. (1)、求证:CF=EB.(2)、若AB=12,AF=8,求CF的长.30. 如图 是一个锐角.
(1)、求证:CF=EB.(2)、若AB=12,AF=8,求CF的长.30. 如图 是一个锐角. (1)、用尺规作图法作出 的平分线 ;(2)、若点P是 上一点,过点P作 于点D, 于点E,求证: .31. 如图,已知点O为△ABC的内心,连AO、BO、CO,过点O的直线分别交边AB、AC于点M、N,
(1)、用尺规作图法作出 的平分线 ;(2)、若点P是 上一点,过点P作 于点D, 于点E,求证: .31. 如图,已知点O为△ABC的内心,连AO、BO、CO,过点O的直线分别交边AB、AC于点M、N,
图一 图二
(1)若∠BAC=70°,那么∠BOC等于多少度?
(2)如图1,若MN∥BC,BM=2,CN=3,求线段MN的长;
(3)如图2,若MN⊥AO,BM=2,CN=3,求线段MN的长.
32. △ABC中,AD为角平分线,DE⊥AB于E,DF⊥AC于F,AB=10cm,AC=8cm,△ABC的面积为54cm2 , 求DE的长.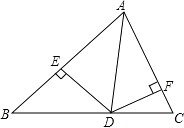 33. 已知:如图 中, .
33. 已知:如图 中, .求作:点P , 使得点P在 上,且点P到 的距离等于 .
作法:
①以点B为圆心,以任意长为半径作弧,分别交射线 于点 ;
②分别以点 为圆心,以大于 的长为半径作弧,两弧在 内部交于点F;
③作射线 交 于点P . 则点P即为所求.
 (1)、使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面证明.
(1)、使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面证明.证明:连接 .
在 和 中
.
()(填推理的依据).
,点P在 上,
.
作 于点Q ,
点P在 上,
()(填推理的依据).