备考2022年中考数学一轮复习(湘教版)专题39 三角形,等腰三角形,线段的垂直平分线
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
1. 如图,已知直线AB和AB上的一点C , 过点C作直线AB的垂线,步骤如下:
第一步:以点C为圆心,以任意长为半径作弧,交直线AB于点D和点E;
第二步:分别以点D和点E为圆心,以 为半径作弧,两弧交于点F;
第三步:作直线CF , 直线CF即为所求.
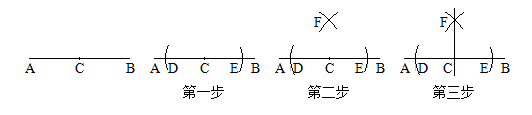
下列关于 的说法正确的是( )
A、 ≥ B、 ≤ C、 D、2. 如图,在△ABC中,AB=AC,分别以点A,B为圆心,大于 AB的长为半径画弧,两弧相交于点M和点N,作直线MN分别交BC、AB于点D和点E,若∠B=50°,则∠CAD的度数是( )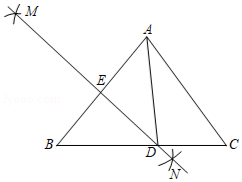 A、30° B、40° C、50° D、60°3. 如图,在△ABC中,AC>BC,分别以点A,B为圆心,以大于 AB的长为半径画弧,两弧交于D,E,经过D,E作直线分别交AB,AC于点M,N,连接BN,下列结论正确的是( )
A、30° B、40° C、50° D、60°3. 如图,在△ABC中,AC>BC,分别以点A,B为圆心,以大于 AB的长为半径画弧,两弧交于D,E,经过D,E作直线分别交AB,AC于点M,N,连接BN,下列结论正确的是( )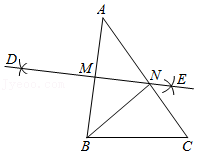 A、AN=NC B、AN=BN C、MN= BC D、BN平分∠ABC4. 如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( )
A、AN=NC B、AN=BN C、MN= BC D、BN平分∠ABC4. 如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( ) A、10.5 B、12 C、15 D、185. 如图,已知线段 ,利用尺规作 的垂直平分线,步骤如下:①分别以点 为圆心,以 的长为半径作弧,两弧相交于点 和 .②作直线 .直线 就是线段 的垂直平分线.则 的长可能是( )
A、10.5 B、12 C、15 D、185. 如图,已知线段 ,利用尺规作 的垂直平分线,步骤如下:①分别以点 为圆心,以 的长为半径作弧,两弧相交于点 和 .②作直线 .直线 就是线段 的垂直平分线.则 的长可能是( ) A、1 B、2 C、3 D、46. 在 中, , .用无刻度的直尺和圆规在BC边上找一点D , 使 为等腰三角形.下列作法错误的是( )A、
A、1 B、2 C、3 D、46. 在 中, , .用无刻度的直尺和圆规在BC边上找一点D , 使 为等腰三角形.下列作法错误的是( )A、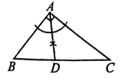 B、
B、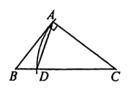 C、
C、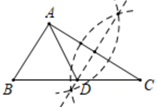 D、
D、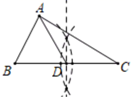 7. 下列长度的三条线段能组成三角形的是( )A、1,2.5,3.5 B、4,6,10 C、20,11,8 D、5,8,128. 下例图形中,具有稳定性的是( )A、
7. 下列长度的三条线段能组成三角形的是( )A、1,2.5,3.5 B、4,6,10 C、20,11,8 D、5,8,128. 下例图形中,具有稳定性的是( )A、 B、
B、 C、
C、 D、
D、 9. 三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
9. 三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )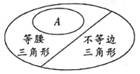 A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形10. 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形10. 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定二、填空题
-
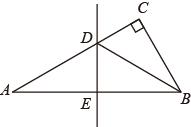
11. 如图,在 中, , ,线段AB的垂直平分线分别交AC、AB于点D、E , 连结BD . 若 ,则AD的长为 .
 12. 如图,已知线段 长为4.现按照以下步骤作图:①分别以点 , 为圆心,大于 长为半径画弧,两弧分别相交于点 , ;②过 , 两点作直线,与线段 相交于点 .则 的长为.
12. 如图,已知线段 长为4.现按照以下步骤作图:①分别以点 , 为圆心,大于 长为半径画弧,两弧分别相交于点 , ;②过 , 两点作直线,与线段 相交于点 .则 的长为.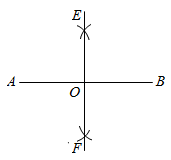 13. 如图,在 中, , ,分别以点A,B为圆心,大于 的长为半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,连接BD,则 .
13. 如图,在 中, , ,分别以点A,B为圆心,大于 的长为半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,连接BD,则 .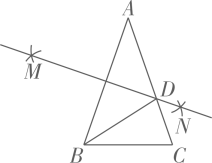 14. 如图,在△ABC中,∠ACB=90°,AC<BC.分别以点A,B为圆心,大于 AB的长为半径画弧,两弧交于D,E两点,直线DE交BC于点F,连接AF.以点A为圆心,AF为半径画弧,交BC延长线于点H,连接AH.若BC=3,则△AFH的周长为 .
14. 如图,在△ABC中,∠ACB=90°,AC<BC.分别以点A,B为圆心,大于 AB的长为半径画弧,两弧交于D,E两点,直线DE交BC于点F,连接AF.以点A为圆心,AF为半径画弧,交BC延长线于点H,连接AH.若BC=3,则△AFH的周长为 .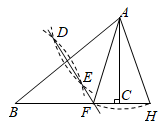 15. 如图,在△ABC中,AB=5,AC=7,直线DE垂直平分BC,垂足为E,交AC于点D,则△ABD的周长是.
15. 如图,在△ABC中,AB=5,AC=7,直线DE垂直平分BC,垂足为E,交AC于点D,则△ABD的周长是.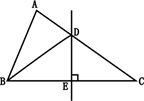 16. 在等腰△ABC 中,AD⊥BC 交直线 BC 于点 D.若 AD=0.5BC,则△ABC 的顶角的度数为
16. 在等腰△ABC 中,AD⊥BC 交直线 BC 于点 D.若 AD=0.5BC,则△ABC 的顶角的度数为三、解答题
-
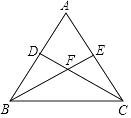
17. 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D.
求证:AD=BC.
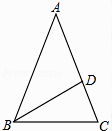 18. 如图,在四边形ABCD中,AD∥BC,对角线AC的中点为O,过点O作AC的垂线分别与AD、BC相交于点E、F,连接AF.求证:AE=AF.
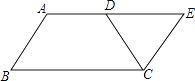
18. 如图,在四边形ABCD中,AD∥BC,对角线AC的中点为O,过点O作AC的垂线分别与AD、BC相交于点E、F,连接AF.求证:AE=AF.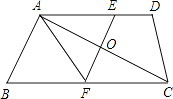 19. 如图,等腰梯形ABCD中,AD∥BC,点E是AD延长线上的一点,且CE=CD.
19. 如图,等腰梯形ABCD中,AD∥BC,点E是AD延长线上的一点,且CE=CD.求证:∠B=∠E.
 20. 求证:等腰三角形的两个底角相等
20. 求证:等腰三角形的两个底角相等(请根据图用符号表示已知和求证,并写出证明过程)
已知:
求证:
证明:
 21. 在等边△ABC中,点D,E分别在边BC、AC上,若CD=2,过点D作DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,求EF的长.
21. 在等边△ABC中,点D,E分别在边BC、AC上,若CD=2,过点D作DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,求EF的长.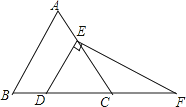 22.
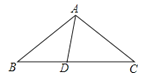
22.如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数;
(2)求证:DC=AB.
 23.
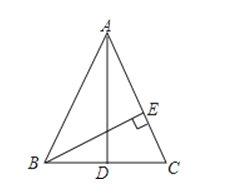
23.如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
四、综合题
-
24.(1)、如图,已知 为边 上一点,请用尺规作图的方法在边 上求作一点 .使 .(保留作图痕迹,不写作法)
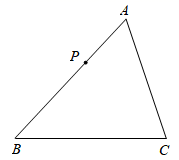 (2)、在上图中,如果 ,则 的周长是 .25. 《淮南子・天文训》中记载了一种确定东西方向的方法,大意是:日出时,在地面上点 处立一根杆,在地面上沿着杆的影子的方向取一点 ,使 两点间的距离为10步(步是古代的一种长度单位),在点 处立一根杆;日落时,在地面上沿着点 处的杆的影子的方向取一点 ,使 两点间的距离为10步,在点 处立一根杆.取 的中点 ,那么直线 表示的方向为东西方向.(1)、上述方法中,杆在地面上的影子所在直线及点 的位置如图所示.使用直尺和圆规,在图中作 的中点 (保留作图痕迹);
(2)、在上图中,如果 ,则 的周长是 .25. 《淮南子・天文训》中记载了一种确定东西方向的方法,大意是:日出时,在地面上点 处立一根杆,在地面上沿着杆的影子的方向取一点 ,使 两点间的距离为10步(步是古代的一种长度单位),在点 处立一根杆;日落时,在地面上沿着点 处的杆的影子的方向取一点 ,使 两点间的距离为10步,在点 处立一根杆.取 的中点 ,那么直线 表示的方向为东西方向.(1)、上述方法中,杆在地面上的影子所在直线及点 的位置如图所示.使用直尺和圆规,在图中作 的中点 (保留作图痕迹); (2)、在如图中,确定了直线 表示的方向为东西方向.根据南北方向与东西方向互相垂直,可以判断直线 表示的方向为南北方向,完成如下证明.
(2)、在如图中,确定了直线 表示的方向为东西方向.根据南北方向与东西方向互相垂直,可以判断直线 表示的方向为南北方向,完成如下证明.证明:在 中, ▲ , 是 的中点,
▲ (填推理的依据).
∵直线 表示的方向为东西方向,
∴直线 表示的方向为南北方向.
26. 如图,△ABC是边长为12cm的等边三角形,动点M、N同时从A、B两点出发,分别沿AB、BC方向匀速移动.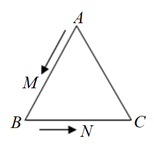 (1)、若点M的运动速度是2cm/s,点N的运动速度是4cm/s,当N到达点C时,M、N两点都停止运动,设运动时间为t(s),当t=2时,判断△BMN的形状,并说明理由;(2)、当它们的速度都是2cm/s,当点M到达点B时,M、N两点停止运动,设点M的运动时间为t(s),则当t为何值时,△MBN是直角三角形?27. 问题:如图,在△ABD中,BA=BD,在BD的延长线上取点E,C,作△AEC,使EA=EC。若∠BAE=90°,∠B=45°,求∠DAC的度数。
(1)、若点M的运动速度是2cm/s,点N的运动速度是4cm/s,当N到达点C时,M、N两点都停止运动,设运动时间为t(s),当t=2时,判断△BMN的形状,并说明理由;(2)、当它们的速度都是2cm/s,当点M到达点B时,M、N两点停止运动,设点M的运动时间为t(s),则当t为何值时,△MBN是直角三角形?27. 问题:如图,在△ABD中,BA=BD,在BD的延长线上取点E,C,作△AEC,使EA=EC。若∠BAE=90°,∠B=45°,求∠DAC的度数。答案:∠DAC=45°。
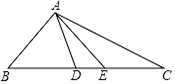
思考:
(1)、如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?说明理由。(2)、如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数。28. 已知:如图,AB、AC是⊙O的两条弦,且AB=AC,D是AO延长线上一点,联结BD并延长交⊙O于点E,联结CD并延长交⊙O于点F.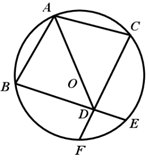 (1)、求证:BD=CD:(2)、如果AB2=AO·AD,求证:四边形ABDC是菱形.29. 如图,在△ABC中,AC<AB<BC.
(1)、求证:BD=CD:(2)、如果AB2=AO·AD,求证:四边形ABDC是菱形.29. 如图,在△ABC中,AC<AB<BC.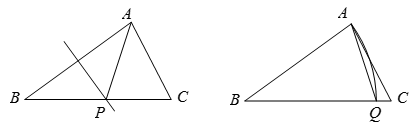 (1)、已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B.(2)、以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q.连接AQ若∠AQC=3∠B,求∠B的度数.30. 如图, 中, ,小聪同学利用直尺和圆规完成了如下操作:
(1)、已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B.(2)、以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q.连接AQ若∠AQC=3∠B,求∠B的度数.30. 如图, 中, ,小聪同学利用直尺和圆规完成了如下操作:①作 的平分线 交 于点 ;
②作边 的垂直平分线 , 与 相交于点 ;
③连接 , .
请你观察图形解答下列问题:
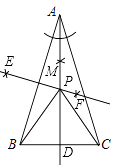 (1)、线段 , , 之间的数量关系是;(2)、若 ,求 的度数.31. 数学课上,张老师举了下面的例题:
(1)、线段 , , 之间的数量关系是;(2)、若 ,求 的度数.31. 数学课上,张老师举了下面的例题:例1 等腰三角形 中, ,求 的度数.(答案: )
例2 等腰三角形 中, ,求 的度数.(答案: 或 或 )
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形 中, ,求 的度数.
(1)、请你解答以上的变式题.(2)、解(1)后,小敏发现, 的度数不同,得到 的度数的个数也可能不同.如果在等腰三角形 中,设 ,当 有三个不同的度数时,请你探索 的取值范围.32. 数学课上,张老师举了下面的例题:例1:等腰三角形ABC中,∠A=110°,求∠B的度数。(答案:35°)
例2:等腰三角形ABC中,∠A=40°,求∠B的度数。(答案:40°或70°或100°)
张老师启发同学们进行变式,小敏编了如下一题:
变式:等腰三角形ABC中,∠A=80°,求∠B的度数
(1)、请你解答以上的表式题。(2)、解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同。如果在等腰三角形ABC中,设∠A=x0 , 当∠B有三个不同的度数时,请你探索x的取值范围。