备考2022年中考数学一轮复习(湘教版)专题34 二次函数的应用
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
1. 如图,已知抛物线 与直线 交于 , 两点,则关于 的不等式 的解集是( )
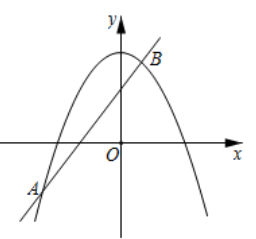 A、 或 B、 或 C、 D、2. 将二次函数 的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线 与新函数的图象恰有3个公共点时,b的值为( )
A、 或 B、 或 C、 D、2. 将二次函数 的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线 与新函数的图象恰有3个公共点时,b的值为( )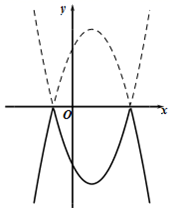 A、 或 B、 或 C、 或 D、 或3. 二次函数 的图象与一次函数 在同一平面直角坐标系中的图象可能是( )A、
A、 或 B、 或 C、 或 D、 或3. 二次函数 的图象与一次函数 在同一平面直角坐标系中的图象可能是( )A、 B、
B、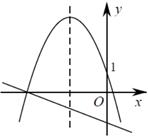 C、
C、 D、
D、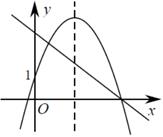 4. 对于一个函数,当自变量x取a时,其函数值y等于2a,我们称a为这个函数的二倍数.若二次函数y=x2+x+c(c为常数)有两个不相等且小于1的二倍数,则c的取值范围是( )A、c< B、0<c< C、﹣1<c< D、﹣1<c<05. 对于一个函数自变量x取c时,函数值为0,则称c为这个函数的零点.若关于x的二次函数 有两个不相等的零点 , ,关于x的方程 有两个不相等的非零实数根 和 ,则下列式子一定正确的是( )A、 B、 C、 D、6. 已知二次函数 的图象经过 与 两点,关于 的方程 有两个根,其中一个根是5.则关于 的方程 有两个整数根,这两个整数根是( )A、-2或4 B、-2或0 C、0或4 D、-2或57. 如图,矩形 中, , ,抛物线 的顶点 在矩形 内部或其边上,则 的取值范围是( )
4. 对于一个函数,当自变量x取a时,其函数值y等于2a,我们称a为这个函数的二倍数.若二次函数y=x2+x+c(c为常数)有两个不相等且小于1的二倍数,则c的取值范围是( )A、c< B、0<c< C、﹣1<c< D、﹣1<c<05. 对于一个函数自变量x取c时,函数值为0,则称c为这个函数的零点.若关于x的二次函数 有两个不相等的零点 , ,关于x的方程 有两个不相等的非零实数根 和 ,则下列式子一定正确的是( )A、 B、 C、 D、6. 已知二次函数 的图象经过 与 两点,关于 的方程 有两个根,其中一个根是5.则关于 的方程 有两个整数根,这两个整数根是( )A、-2或4 B、-2或0 C、0或4 D、-2或57. 如图,矩形 中, , ,抛物线 的顶点 在矩形 内部或其边上,则 的取值范围是( )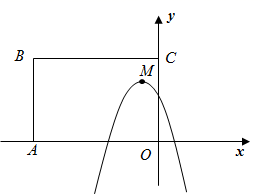 A、 B、 C、 D、8. 如图,抛物线 的对称轴为直线 ,若关于 的一元二次方程 ( 为实数)在 的范围内有解,则 的取值错误的是( )
A、 B、 C、 D、8. 如图,抛物线 的对称轴为直线 ,若关于 的一元二次方程 ( 为实数)在 的范围内有解,则 的取值错误的是( )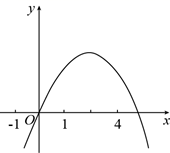 A、 B、 C、 D、9. 如图,抛物线y=ax2﹣2ax﹣3a(a≠0)与x轴交于点A , B . 与y轴交于点C . 连接AC、BC . 已知△ABC的面积为3.将抛物线向左平移h(h>0)个单位,记平移后抛物线中y随着x的增大而增大的部分为H . 当直线BC与H没有公共点时,h的取值范围是( )
A、 B、 C、 D、9. 如图,抛物线y=ax2﹣2ax﹣3a(a≠0)与x轴交于点A , B . 与y轴交于点C . 连接AC、BC . 已知△ABC的面积为3.将抛物线向左平移h(h>0)个单位,记平移后抛物线中y随着x的增大而增大的部分为H . 当直线BC与H没有公共点时,h的取值范围是( )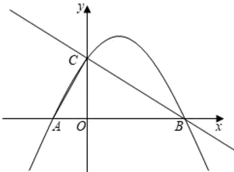 A、h> B、0<h≤ C、h>2 D、0<h<210. 某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,每人的单价就降低10元,若这个旅行社要获得最大营业额,此时旅行团人数为( )人A、56 B、55 C、54 D、53
A、h> B、0<h≤ C、h>2 D、0<h<210. 某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,每人的单价就降低10元,若这个旅行社要获得最大营业额,此时旅行团人数为( )人A、56 B、55 C、54 D、53二、填空题
-
11. 从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度 (单位: )与它距离喷头的水平距离 (单位: )之间满足函数关系式 ,喷出水珠的最大高度是 .
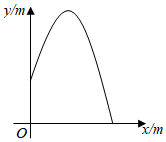 12. 以初速度v(单位:m/s)从地面竖直向上抛出小球,从抛出到落地的过程中,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=vt﹣4.9t2.现将某弹性小球从地面竖直向上抛出,初速度为v1 , 经过时间t1落回地面,运动过程中小球的最大高度为h1(如图1);小球落地后,竖直向上弹起,初速度为v2 , 经过时间t2落回地面,运动过程中小球的最大高度为h2(如图2).若h1=2h2 , 则t1:t2=.
12. 以初速度v(单位:m/s)从地面竖直向上抛出小球,从抛出到落地的过程中,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=vt﹣4.9t2.现将某弹性小球从地面竖直向上抛出,初速度为v1 , 经过时间t1落回地面,运动过程中小球的最大高度为h1(如图1);小球落地后,竖直向上弹起,初速度为v2 , 经过时间t2落回地面,运动过程中小球的最大高度为h2(如图2).若h1=2h2 , 则t1:t2=. 13. 某快餐店销售A、B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是元.14. 已知在平面直角坐标系xOy中,点A的坐标为(3,4),M是抛物线 ( )对称轴上的一个动点。小明经探究发现:当 的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定。若抛物线 ( )的对称轴上存在3个不同的点M,使△AOM为直角三角形,则 的值是15. 如图,点A(0,1),平行于x轴的直线AC分别交抛物线 与 (x≥0)于B、C两点,过点C作y轴的平行线交 于点D , 直线DE∥AC , 交 于点E , 则DE= .
13. 某快餐店销售A、B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是元.14. 已知在平面直角坐标系xOy中,点A的坐标为(3,4),M是抛物线 ( )对称轴上的一个动点。小明经探究发现:当 的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定。若抛物线 ( )的对称轴上存在3个不同的点M,使△AOM为直角三角形,则 的值是15. 如图,点A(0,1),平行于x轴的直线AC分别交抛物线 与 (x≥0)于B、C两点,过点C作y轴的平行线交 于点D , 直线DE∥AC , 交 于点E , 则DE= . 16. 如图,直线 与抛物线 交于点 ,且点A在y轴上,点B在x轴上,则不等式 的解集为 .
16. 如图,直线 与抛物线 交于点 ,且点A在y轴上,点B在x轴上,则不等式 的解集为 .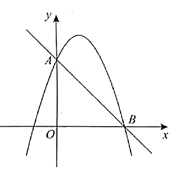
三、解答题
-
17. 端午节前夕,三位同学到某超市调研一种进价为80元的粽子礼盒的销售情况,请根据小梅提供的信息,解答小慧和小杰提出的问题.(价格取正整数)
 18.
18.如图1,在△ABC中,∠A=30°,点P从点A出发以2cm/s的速度沿折线A—C—B运动,点Q从点A出发以a(cm/s)的速度沿AB运动,P,Q两点同时出发,当某一点运动到点B时,两点同时停止运动.设运动时间为x(s),△APQ的面积为y(cm2),y关于x的函数图象由C1 , C2两段组成,如图2所示.
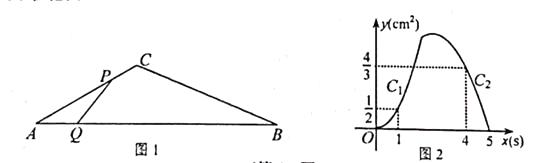 (1)、求a的值;(2)、求图2中图象C2段的函数表达式;(3)、当点P运动到线段BC上某一段时△APQ的面积,大于当点P在线段AC上任意一点时△APQ的面积,求x的取值范围.19.
(1)、求a的值;(2)、求图2中图象C2段的函数表达式;(3)、当点P运动到线段BC上某一段时△APQ的面积,大于当点P在线段AC上任意一点时△APQ的面积,求x的取值范围.19.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分. 如图,甲 在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式 ,已知点O与球网的水平距离为5m,球网的高度1.55m.
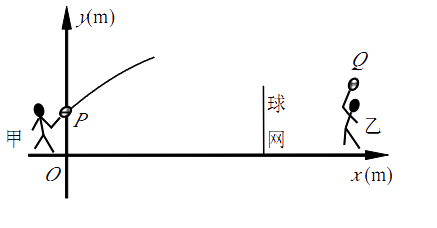 (1)、当a=− 时,①求h的值.②通过计算判断此球能否过网.(2)、若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 m的Q处时,乙扣球成功,求a的值.20. 某商场购进一批L型服装(数量足够多),进价为40元/件,以60元/件销售,每天销售20件,根据市场调研,若每件降价1元,则每天销售数量比原来多3件.现商场决定对L型服装开展降价促销活动,每件降价x元(x为正整数).在促销期间,商场要想每天获得最大销售毛利润,每件应降价多少元?每天最大销售毛利润为多少?(注:每件服装销售毛利润是指每件服装的销售价与进货价的差)21. 某商场在1月至12月份经销某种品牌的服装,由于受到时令的影响,该种服装的销售情况如下:销售价格y1(元/件)与销售月份x(月)的关系大致满足如图的函数,销售成本y2(元/件)与销售月份x(月)满足y2=
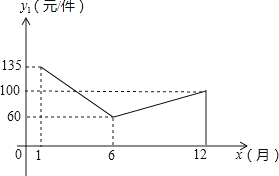
(1)、当a=− 时,①求h的值.②通过计算判断此球能否过网.(2)、若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 m的Q处时,乙扣球成功,求a的值.20. 某商场购进一批L型服装(数量足够多),进价为40元/件,以60元/件销售,每天销售20件,根据市场调研,若每件降价1元,则每天销售数量比原来多3件.现商场决定对L型服装开展降价促销活动,每件降价x元(x为正整数).在促销期间,商场要想每天获得最大销售毛利润,每件应降价多少元?每天最大销售毛利润为多少?(注:每件服装销售毛利润是指每件服装的销售价与进货价的差)21. 某商场在1月至12月份经销某种品牌的服装,由于受到时令的影响,该种服装的销售情况如下:销售价格y1(元/件)与销售月份x(月)的关系大致满足如图的函数,销售成本y2(元/件)与销售月份x(月)满足y2=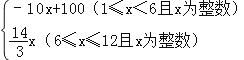 , 月销售量y3(件)与销售月份x(月)满足y3=10x+20.
, 月销售量y3(件)与销售月份x(月)满足y3=10x+20.(1)根据图象求出销售价格y1(元/件)与销售月份x(月)之间的函数关系式;(6≤x≤12且x为整数)
(2)求出该服装月销售利润W(元)与月份x(月)之间的函数关系式,并求出哪个月份的销售利润最大?最大利润是多少?(6≤x≤12且x为整数)
 22. 某旅游景点的门票价格是20元/人,日接待游客500人,进入旅游旺季时,景点想提高门票价格增加盈利.经过市场调查发现,门票价格每提高5元,日接待游客人数就会减少50人.设提价后的门票价格为x(元/人)(x>20),日接待游客的人数为y(人).
22. 某旅游景点的门票价格是20元/人,日接待游客500人,进入旅游旺季时,景点想提高门票价格增加盈利.经过市场调查发现,门票价格每提高5元,日接待游客人数就会减少50人.设提价后的门票价格为x(元/人)(x>20),日接待游客的人数为y(人).(1)求y与x(x>20)的函数关系式;
(2)已知景点每日的接待成本为z(元),z与y满足函数关系式:z=100+10y.求z与x的函数关系式;
(3)在(2)的条件下,当门票价格为多少时,景点每日获取的利润最大?最大利润是多少?(利润=门票收入﹣接待成本)
四、综合题
-
23. 如图①,在 中, 于点 , , , 点 是 上一动点(不与点 , 重合),在 内作矩形 ,点 在 上,点 , 在 上,设 ,连接 .
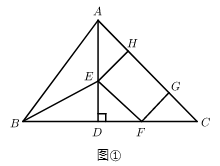
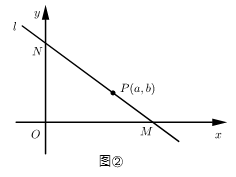 (1)、当矩形 是正方形时,直接写出 的长;(2)、设 的面积为 ,矩形 的面积为 ,令 ,求 关于 的函数解析式(不要求写出自变量 的取值范围);(3)、如图②,点 是(2)中得到的函数图象上的任意一点,过点 的直线 分别与 轴正半轴, 轴正半轴交于 , 两点,求 面积的最小值,并说明理由.24. 为增加农民收入,助力乡村振兴.某驻村干部指导农户进行草莓种植和销售,已知草莓的种植成本为8元/千克,经市场调查发现,今年五一期间草莓的销售量y(千克)与销售单价x(元/千克)(8≤x≤40)满足的函数图象如图所示.
(1)、当矩形 是正方形时,直接写出 的长;(2)、设 的面积为 ,矩形 的面积为 ,令 ,求 关于 的函数解析式(不要求写出自变量 的取值范围);(3)、如图②,点 是(2)中得到的函数图象上的任意一点,过点 的直线 分别与 轴正半轴, 轴正半轴交于 , 两点,求 面积的最小值,并说明理由.24. 为增加农民收入,助力乡村振兴.某驻村干部指导农户进行草莓种植和销售,已知草莓的种植成本为8元/千克,经市场调查发现,今年五一期间草莓的销售量y(千克)与销售单价x(元/千克)(8≤x≤40)满足的函数图象如图所示.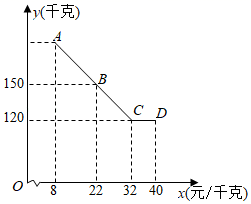 (1)、根据图象信息,求y与x的函数关系式;(2)、求五一期间销售草莓获得的最大利润.25. 为了实施乡村振兴战略,帮助农民增加收入,市政府大力扶持农户发展种植业,每亩土地每年发放种植补贴120元.张远村老张计划明年承租部分土地种植某种经济作物.考虑各种因素,预计明年每亩土地种植该作物的成本y(元)与种植面积x(亩)之间满足一次函数关系,且当 时, ;当 时, .(1)、求y与x之间的函数关系式(不求自变量的取值范围);(2)、受区域位置的限制,老张承租土地的面积不得超过240亩.若老张明年销售该作物每亩的销售额能达到2160元,当种植面积为多少时,老张明年种植该作物的总利润最大?最大利润是多少?(每亩种植利润=每亩销售额-每亩种植成本+每亩种植补贴)26. 如图1是一座抛物线型拱桥侧面示意图.水面宽AB与桥长CD均为24m,在距离D点6米的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.
(1)、根据图象信息,求y与x的函数关系式;(2)、求五一期间销售草莓获得的最大利润.25. 为了实施乡村振兴战略,帮助农民增加收入,市政府大力扶持农户发展种植业,每亩土地每年发放种植补贴120元.张远村老张计划明年承租部分土地种植某种经济作物.考虑各种因素,预计明年每亩土地种植该作物的成本y(元)与种植面积x(亩)之间满足一次函数关系,且当 时, ;当 时, .(1)、求y与x之间的函数关系式(不求自变量的取值范围);(2)、受区域位置的限制,老张承租土地的面积不得超过240亩.若老张明年销售该作物每亩的销售额能达到2160元,当种植面积为多少时,老张明年种植该作物的总利润最大?最大利润是多少?(每亩种植利润=每亩销售额-每亩种植成本+每亩种植补贴)26. 如图1是一座抛物线型拱桥侧面示意图.水面宽AB与桥长CD均为24m,在距离D点6米的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.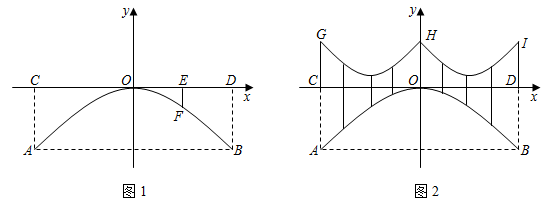 (1)、求桥拱项部O离水面的距离.(2)、如图2,桥面上方有3根高度均为4m的支柱CG,OH,DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为1m.
(1)、求桥拱项部O离水面的距离.(2)、如图2,桥面上方有3根高度均为4m的支柱CG,OH,DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为1m.①求出其中一条钢缆抛物线的函数表达式.
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求彩带长度的最小值.
27. 渠县是全国优质黄花主产地,某加工厂加工黄花的成本为30元/千克,根据市场调查发现,批发价定为48元/千克时,每天可销售500千克.为增大市场占有率,在保证盈利的情况下,工厂采取降价措施.批发价每千克降低1元,每天销量可增加50千克.(1)、写出工厂每天的利润 元与降价 元之间的函数关系.当降价2元时,工厂每天的利润为多少元?(2)、当降价多少元时,工厂每天的利润最大,最大为多少元?(3)、若工厂每天的利润要达到9750元,并让利于民,则定价应为多少元?28. 某商贸公司购进某种商品的成本为20元/ ,经过市场调研发现,这种商品在未来40天的销售单价y(元/ )与时间x(天)之间的函数关系式为: 且x为整数,且日销量 与时间x(天)之间的变化规律符合一次函数关系,如下表:时间x(天)
1
3
6
10
…
日销量
142
138
132
124
…
填空:
(1)、m与x的函数关系为;(2)、哪一天的销售利润最大?最大日销售利润是多少?(3)、在实际销售的前20天中,公司决定每销售 商品就捐赠n元利润( )给当地福利院,后发现:在前20天中,每天扣除捐赠后的日销售利润随时间x的增大而增大,求n的取值范围.29. 已知抛物线 与x轴交于点A、B(其中A在点B的左侧),与y轴交于点C.(1)、求点B、C的坐标;(2)、设点 与点C关于该抛物线的对称轴对称在y轴上是否存在点P,使 与 相似且 与 是对应边?若存在,求点P的坐标;若不存在,请说明理由.