备考2022年中考数学一轮复习（湘教版）专题33 二次函数与一元二次方程的联系

试卷更新日期：2021-09-22 类型：一轮复习

进入出卷网下载

一、单选题

1. 直线l过点（0，4）且与y轴垂直，若二次函数 $y = （ x-a ）^{2} + （ x-2a ）^{2} + （ x-3a ）^{2} - 2 a {}^{2}+ a$ （其中x是自变量）的图象与直线l有两个不同的交点，且其对称轴在y轴右侧，则a的取值范围是（）

A、a＞4 B、a＞0 C、0＜a≤4 D、0＜a＜4

查看试题解析
2. 已知二次函数 $y = a x^{2} + b x + c$ 的图象经过 $(- 3 ， 0)$ 与 $(1 ， 0)$ 两点，关于x的方程 $a x^{2} + b x + c + m = 0$ $(m > 0)$ 有两个根，其中一个根是3.则关于x的方程 $a x^{2} + b x + c + n = 0$ $(0 < n < m)$ 有两个整数根，这两个整数根是（）

A、-2或0 B、-4或2 C、-5或3 D、-6或4

查看试题解析
3. 在平面直角坐标系中，已知函数y₁=x²+ax+1，y₂=x²+bx+2，y₃=x²+cx+4，其中a，b，c是正实数，且满足b²=ac。设函数y₁ ， y₂ ， y₃的图象与x轴的交点个数分别为M₁ ， M₂ ， M₃ ，（）

A、若M₁=2，M₂=2，则M₃=0 B、若M₁=1，M₂=0，则M₃=0 C、若M₁=0，M₂=2，则M₃=0 D、若M₁=0，M₂=0，则M₃=0

查看试题解析
4. 已知m＞0，关于x的一元二次方程（x+1）（x﹣2）﹣m＝0的解为x₁ ， x₂（x₁＜x₂），则下列结论正确的是（）

A、x₁＜﹣1＜2＜x₂ B、﹣1＜x₁＜2＜x₂ C、﹣1＜x₁＜x₂＜2 D、x₁＜﹣1＜x₂＜2

查看试题解析
5. 设一元二次方程（x-1）（x-2）=m（m＜0）的两根分别为α，β，且α＜β，则α，β满足（）

A、1＜α＜β＜2 B、1＜α＜2＜β C、α＜1＜β＜2 D、α＜1且β＞2

查看试题解析

二、填空题

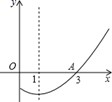
6. 函数y₁＝（x+1）（x﹣2a）（a为常数）图像与x轴相交于点（x₁ ， 0）（x₂ ， 0），函数y₂＝x﹣a的图像与x轴相交于点（x₃ ， 0），若x₁＜x₃＜x₂ ，则a的取值范围为．

查看试题解析
7. 如图是二次函数 $y = a x^{2} + b x + c$ 图象的一部分，其对称轴为直线 $x = 1$ ，若其与 $x$ 轴一交点为 $A (3 ， 0)$ ，则由图象可知，方程 $a x^{2} + b x + c = 0$ 的解是.

查看试题解析
8. 抛物线y＝ax²＋bx＋c经过A（﹣1，4），B（2，4），则关于x的一元二次方程a（x﹣3）²﹣4＝3b﹣bx﹣c的解为.

查看试题解析
9. 若一元二次方程2x²﹣2x+m＝0有实数根，则m的取值范围是.

查看试题解析
10. 已知抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴交点的坐标分别为 $(- 1, 0)$ ， $(3, 0)$ ，则一元二次方程 $x^{2} + b x + c = 0$ 的根为.

查看试题解析
11. 已知抛物线y=a(x－h)²＋k与x轴交于(－2,0)、(3,0)，则关于x的一元二次方程：a(x＋h＋6)²＋k=0的解为.

查看试题解析

三、解答题

12.
甲、乙两企业去年末都有利润积累，甲企业利润为300万元，甲企业认为：企业要可持续发展，必须进行自主创新和技术改造，由于投资更新等原因，甲企业的利润积累y_甲（万元）与时间x（年）之间的函数图象呈抛物线（如图）乙企业的利润积累y_乙（万元）每年增加50万元，预计第一年末（今年末）利润积累150万元．
（1）乙企业去年末的利润积累是多少万元，乙企业利润积累y_乙（万元）与时间x（年）之间的函数关系式为（不必写出自变量x的取值范围）．
（2）到第几年末，甲企业的利润积累重新达到去年末与乙企业利润积累的倍数关系？
（3）改造初期，甲企业的利润积累逐渐减少，甚至会低于乙企业的利润积累．随着甲企业进入改造成长期，甲企业的利润积累重新高于乙企业的利润积累，试问第几年（保留整数位．参考数据： $\sqrt{13}$ ≈3.6）甲企业开始进入改造成长期？5年后（含5年）甲企业进入改造成熟期，效益将显现出来．改造成熟期，甲企业的利润积累最少会高于乙企业的利润积累多少万元？

查看试题解析
13. 利用二次函数的图象求方程x²+2x﹣4=0的近似根

查看试题解析
14. 已知抛物线 $y = a x^{2} + b x + c$ 经过 $A (- 3, 0)$ 、 $B (4, 0)$ 两点，求关于x的一元二次方程 $a {(x - 1)}^{2} + c = b - b x$ 的解.

查看试题解析
15. 某公司生产A种产品，它的成本是6元/件，售价是8元/件，年销售量为5万件．为了获得更好的效益，公司准备拿出一定的资金做广告，根据经验，每年投入的广告费是x万元，产品的年销售量将是原销售量的y倍，且y与x之间满足我们学过的二种函数（即一次函数和二次函数）关系中的一种，它们的关系如下表：
x（万元）
0
0.5
1
1.5
2
…
y
1
1.275
1.5
1.675
1.8
…
（1）求y与x的函数关系式（不要求写出自变量的取值范围）
（2）如果把利润看作是销售总额减去成本费用和广告费用，试求出年利润W（万元）与广告费用x（万元）的函数关系式，并计算每年投入的广告费是多少万元时所获得的利润最大？
（3）如果公司希望年利润W（万元）不低于14万元，请你帮公司确定广告费的范围．

查看试题解析

四、综合题

16. 如图，函数 $y = - x^{2} + b x + c$ 的图象经过点 $A (m ， 0)$ ， $B (0 ， n)$ 两点， $m$ ， $n$ 分别是方程 $x^{2} - 2 x - 3 = 0$ 的两个实数根，且 $m < n$ ．

(1)、求 $m$ ， $n$ 的值以及函数的解析式；当 $0 ⩽ x ⩽ 3$ 时，求函数 $y$ 的最大值和最小值；

(2)、设抛物线 $y = - x^{2} + b x + c$ 与 $x$ 轴的另一个交点为 $C$ ，抛物线的顶点为 $D$ ，连接 $A B$ ， $B C$ ， $B D$ ， $C D$ 求证： $△ B C D ∽ △ O B A$ ．

查看试题解析
17. 已知函数y＝x²＋(m－3)x＋1－2m（m为常数）.

(1)、求证：不论m为何值，该函数的图象与x轴总有两个公共点.

(2)、不论m为何值，该函数的图象都会经过一个定点，求定点的坐标.

查看试题解析
18. 二次函数 $y = a x^{2} + b x + 2$ 的图象交x轴于A(-1， 0)，B(4， 0)两点，交y轴于点C.动点M从点A出发，以每秒2个单位长度的速度沿AB方向运动，过点M作MN⊥x轴交直线BC于点N，交抛物线于点D，连接
AC.设运动的时间为t秒.

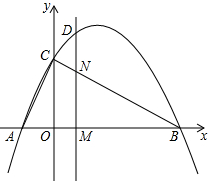(1)、求二次函数 $y = a x^{2} + b x + 2$ 的表达式：

(2)、连接BD，当 $t = \frac{3}{2}$ 时，求△DNB的面积：

(3)、在直线MN上存在一点P，当△PBC是以∠BPC为直角的等腰直角三角形时，求此时点D的坐标；

(4)、当 $t = \frac{5}{4}$ 时，在直线MN上存在一点Q，使得∠AQC+∠OAC=90°，求点Q的坐标，

查看试题解析
19.
科技馆是少年儿童节假日游玩的乐园．如图所示，图中点的横坐标x表示科技馆从8：30开门后经过的时间（分钟），纵坐标y表示到达科技馆的总人数．图中曲线对应的函数解析式为y= $\{\begin{matrix} a x^{2} ， 0 \leq x \leq 30 \\ b {(x - 90)}^{2} + n ， 30 \leq x \leq 90 \end{matrix}$ ，10：00之后来的游客较少可忽略不计．

(1)、请写出图中曲线对应的函数解析式；

(2)、为保证科技馆内游客的游玩质量，馆内人数不超过684人，后来的人在馆外休息区等待．从10：30开始到12：00馆内陆续有人离馆，平均每分钟离馆4人，直到馆内人数减少到624人时，馆外等待的游客可全部进入．请问馆外游客最多等待多少分钟？

查看试题解析
20. 画出函数y=﹣2x²+8x﹣6的图象，根据图象回答：

(1)、方程﹣2x²+8x﹣6=0的解是什么

(2)、当x取何值时，y＞0

(3)、当x取何值时，y＜0

查看试题解析

21. 一个批发商销售成本为20元/千克的某产品，根据物价部门规定：该产品每千克售价不得超过90元，在销售过程中发现的售量y（千克）与售价x（元/千克）满足一次函数关系，对应关系如下表：

售价x（元/千克）	…	50	60	70	80	…
销售量y（千克）	…	100	90	80	70	…

(1)、求y与x的函数关系式；

(2)、该批发商若想获得4000元的利润，应将售价定为多少元？

(3)、该产品每千克售价为多少元时，批发商获得的利润w（元）最大？此时的最大利润为多少元？

查看试题解析

x（万元）	0	0.5	1	1.5	2	…
y	1	1.275	1.5	1.675	1.8	…