备考2022年中考数学一轮复习(湘教版)专题32 二次函数及其图像与性质
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
1. 在平面直角坐标系中,将二次函数 的图象向左平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式为( )A、 B、 C、 D、2. 如图,已如抛物线 开口向上,与 轴的一个交点为 ,对称轴为直线 .下列结论错误的是( )
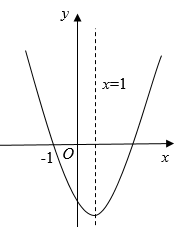 A、 B、 C、 D、3. 已知A、B两点的坐标分别为(3,﹣4)、(0,﹣2),线段AB上有一动点M(m,n),过点M作x轴的平行线交抛物线y=a(x﹣1)2+2于P(x1 , y1)、Q(x2 , y2)两点.若x1<m≤x2 , 则a的取值范围为( )A、﹣4≤a<﹣ B、﹣4≤a≤﹣ C、﹣ ≤a<0 D、﹣ <a<04. 已知二次函数 ,当 时,y随x增大而增大,则实数a的取值范围是( )A、 B、 C、 D、5. 将抛物线y=(x﹣1)2+2向左平移3个单位长度,再向下平移4个单位长度所得到的抛物线的解析式为( )A、y=x2﹣8x+22 B、y=x2﹣8x+14 C、y=x2+4x+10 D、y=x2+4x+26. 已知二次函数y=ax2+bx+c的自变量x与函数y的部分对应值见表格,则下列结论:①c=2;②b2﹣4ac>0;③方程ax2+bx=0的两根为x1=﹣2,x2=0;④7a+c<0.其中正确的有( )
A、 B、 C、 D、3. 已知A、B两点的坐标分别为(3,﹣4)、(0,﹣2),线段AB上有一动点M(m,n),过点M作x轴的平行线交抛物线y=a(x﹣1)2+2于P(x1 , y1)、Q(x2 , y2)两点.若x1<m≤x2 , 则a的取值范围为( )A、﹣4≤a<﹣ B、﹣4≤a≤﹣ C、﹣ ≤a<0 D、﹣ <a<04. 已知二次函数 ,当 时,y随x增大而增大,则实数a的取值范围是( )A、 B、 C、 D、5. 将抛物线y=(x﹣1)2+2向左平移3个单位长度,再向下平移4个单位长度所得到的抛物线的解析式为( )A、y=x2﹣8x+22 B、y=x2﹣8x+14 C、y=x2+4x+10 D、y=x2+4x+26. 已知二次函数y=ax2+bx+c的自变量x与函数y的部分对应值见表格,则下列结论:①c=2;②b2﹣4ac>0;③方程ax2+bx=0的两根为x1=﹣2,x2=0;④7a+c<0.其中正确的有( )x
…
﹣3
﹣2
﹣1
1
2
…
y
…
1.875
3
m
1.875
0
…
A、①④ B、②③ C、③④ D、②④7. 二次函数 的图象过 四个点,下列说法一定正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则8. 已知抛物线 与 轴有两个交点 , ,抛物线 与 轴的一个交点是 ,则 的值是( )A、5 B、1 C、5或1 D、-5或-19. 如图,二次函数 的图象经过点 , ,与y轴交于点C . 下列结论:① ;②当 时,y随x的增大而增大;③ ;④ .
其中正确的个数有( )
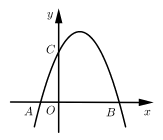 A、1个 B、2个 C、3个 D、4个10. 如图,二次函数 的图象与x轴交于A , 两点,则下列说法正确的是( )
A、1个 B、2个 C、3个 D、4个10. 如图,二次函数 的图象与x轴交于A , 两点,则下列说法正确的是( ) A、 B、点A的坐标为 C、当 时,y随x的增大而减小 D、图象的对称轴为直线
A、 B、点A的坐标为 C、当 时,y随x的增大而减小 D、图象的对称轴为直线二、填空题
-
11. 在函数 中,当x>1时,y随x的增大而 .(填“增大”或“减小”)12. 如图,二次函数 的函数图象经过点(1,2),且与 轴交点的横坐标分别为 、 ,其中 -1< <0,1< <2,下列结论:① ;② ;③ ;④当 时, ;⑤ ,其中正确的有 .(填写正确的序号)
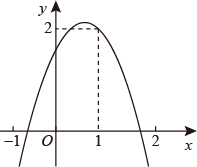 13. 已知y是x的二次函数,如表给出了y与x的几对对应值:
13. 已知y是x的二次函数,如表给出了y与x的几对对应值:x
…
﹣2
﹣1
0
1
2
3
4
…
y
…
11
a
3
2
3
6
11
…
由此判断,表中a=.
14. 将抛物线y=x2﹣2x+3向左平移2个单位长度,所得抛物线为 .15. 在平面直角坐标系 中,若抛物线 与x轴只有一个交点,则 .16. 如图,二次函数 的图象与x轴的正半轴交于点A , 对称轴为直线 ,下面结论: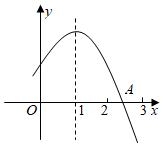
① ;
② ;
③ ;
④方程 必有一个根大于 且小于0.
其中正确的是(只填序号).
17. 把抛物线 向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为 .18. 如图是抛物线y=ax2+bx+c的部分图象,图象过点(3,0),对称轴为直线x=1,有下列四个结论:①abc>0;②a﹣b+c=0;③y的最大值为3;④方程ax2+bx+c+1=0有实数根.其中正确的为 (将所有正确结论的序号都填入).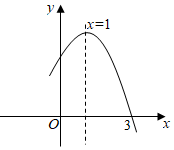
三、解答题
-
19. 已知抛物线y=ax2+bx﹣3(a≠0)经过点(﹣1,0),(3,0),求a,b的值.
20. 如图,抛物线 (a≠0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C , D在抛物线上.设A(t , 0),当t=2时,AD=4.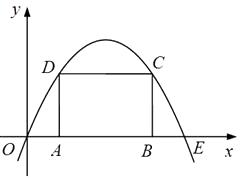 (1)、求抛物线的函数表达式.(2)、当t为何值时,矩形ABCD的周长有最大值?最大值是多少?(3)、保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G , H , 且直线GH平分矩形的面积时,求抛物线平移的距离.21. 当k分别取﹣1,1,2时,函数y=(k﹣1)x2﹣4x+5﹣k都有最大值吗?请写出你的判断,并说明理由;若有,请求出最大值.22. 如图,二次函数y=ax2+bx的图象经过A(1,﹣1)、B(4,0)两点.
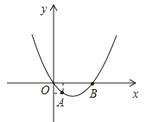
(1)、求抛物线的函数表达式.(2)、当t为何值时,矩形ABCD的周长有最大值?最大值是多少?(3)、保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G , H , 且直线GH平分矩形的面积时,求抛物线平移的距离.21. 当k分别取﹣1,1,2时,函数y=(k﹣1)x2﹣4x+5﹣k都有最大值吗?请写出你的判断,并说明理由;若有,请求出最大值.22. 如图,二次函数y=ax2+bx的图象经过A(1,﹣1)、B(4,0)两点.(1)求这个二次函数解析式;
(2)点M为坐标平面内一点,若以点O、A、B、M为顶点的四边形是平行四边形,请直接写出点M的坐标.
四、综合题
-
23. 已知关于x的二次函数y1=x2+bx+c(实数b,c为常数).(1)、若二次函数的图象经过点(0,4),对称轴为x=1,求此二次函数的表达式;(2)、若b2﹣c=0,当b﹣3≤x≤b时,二次函数的最小值为21,求b的值;(3)、记关于x的二次函数y2=2x2+x+m,若在(1)的条件下,当0≤x≤1时,总有y2≥y1 , 求实数m的最小值.24. 已知抛物线 经过点 和 .(1)、求 、 的值;(2)、将该抛物线向上平移2个单位长度,再向右平移1个单位长度,得到新的抛物线,直接写出新的抛物线相应的函数表达式.25. 抛物线y=﹣x2+bx+c经过点A(﹣3,0)和点C(0,3).
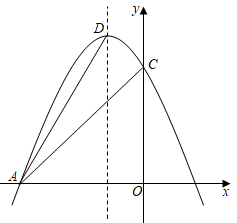
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标( )
(1)、求此抛物线所对应的函数解析式,并直接写出顶点D的坐标;(2)、若过顶点D的直线将△ACD的面积分为1:2两部分,并与x轴交于点Q , 则点Q的坐标为 .26. 如今我国的大棚(如图1)种植技术已十分成熟.小明家的菜地上有一个长为16米的蔬菜大棚,其横截面顶部为抛物线型,大棚的一端固定在离地面高1米的墙体 处,另一端固定在离地面高2米的墙体 处,现对其横截面建立如图2所示的平面直角坐标系.已知大棚上某处离地面的高度 (米)与其离墙体 的水平距离 (米)之间的关系满足 ,现测得 , 两墙体之间的水平距离为6米.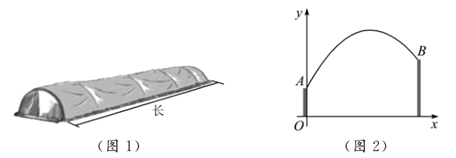 (1)、直接写出 , 的值;(2)、求大棚的最高处到地面的距离;(3)、小明的爸爸欲在大棚内种植黄瓜,需搭建高为 米的竹竿支架若干,已知大棚内可以搭建支架的土地平均每平方米需要4根竹竿,则共需要准备多少根竹竿?
(1)、直接写出 , 的值;(2)、求大棚的最高处到地面的距离;(3)、小明的爸爸欲在大棚内种植黄瓜,需搭建高为 米的竹竿支架若干,已知大棚内可以搭建支架的土地平均每平方米需要4根竹竿,则共需要准备多少根竹竿?
