备考2022年中考数学一轮复习（湘教版）专题31 反比例函数的应用
试卷更新日期：2021-09-22 类型：一轮复习
一、单选题
-
1. 某气球内充满了一定质量 的气体，当温度不变时，气球内气体的气压 （单位： ）是气体体积 （单位： ）的反比例函数： ，能够反映两个变量 和 函数关系的图象是（ ）A、
B、
C、
D、
2. 阿基米德说：“给我一个支点，我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识——杠杆原理，即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为 和 ，则这一杠杆的动力 和动力臂 之间的函数图象大致是（ ）
A、
B、
C、
D、
3.教室里的饮水机接通电源就进入自动程序，开机加热时每分钟上升10℃，加热到100℃，停止加热，水温开始下降，此时水温（℃）与开机后用时（min）成反比例关系．直至水温降至30℃，饮水机关机．饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时，接通电源后，水温y（℃）和时间（min）的关系如图，为了在上午第一节下课时（8：45）能喝到不超过50℃的水，则接通电源的时间可以是当天上午的（ ）
A、7：20 B、7：30 C、7：45 D、7：504. 小明学习了物理中的杠杆平衡原理发现：阻力 阻力臂 动力 动力臂．现已知某一杠杆的阻力和阻力臂分别为2400N和1m，则动力 （单位：N）关于动力臂 （单位：m）的函数图象大致是（ ）A、
B、
C、
D、
5. 已知甲，乙两地相距 （单位： ），汽车从甲地匀速行驶到乙地，则汽车行驶的时间 （单位： ）关于行驶速度 （单位： ）的函数图象是（ ）A、
B、
C、
D、
6. 一个直角三角形的两直角边长分别为x、y其面积为2，则y与x之间的关系用图象表示大致为 （ ）A、
B、
C、
D、
7. A，B两城间的距离为15千米，一人行路的平均速度每小时不少于3千米，也不多于5千米，则表示此人由A到B的行路速度x（千米/小时）与所用时间y（小时）的关系y= 的函数图象是（ ）A、
B、
C、
D、
8. 某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压 p(kPa)是气体体积 V(m 3)的反比例函数，其图象如图所示．当气球内的气压大于140kPa时，气球将爆炸，为了安全起见，气体体积应（ ）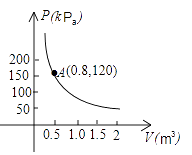
A、不大于 m3 B、不小于 m3 C、不大于 m 3 D、不小于 m 39. 在一个可以改变体积的密闭容器内装有一定质量的某种气体，当改变容器的体积时，气体的密度也会随之改变，密度 （单位： ）与体积V（单位：m3）满足函数关系式 （ 为常数， ），其图象如图所示，则k的值为（ ）
A、9 B、-9 C、4 D、-410. 一张正方形的纸片，剪去两个一样的小矩形得到一个E”图案，如图所示，设小矩形的长和宽分别为x，y，剪去部分的面积为20，若2≤x≤10，则y与x的函数图象是（ ）
A、
B、
C、
D、
二、填空题
-
11. 在温度不变的条件下，一定质量的气体的压强p与它的体积V成反比例，当V=200时，p=50，则当p=25时，V= ．12. 在温度不变的条件下，一定质量的气体的压强p与它的体积V成反比例，当V=200时，P=50，则当P=25时，V=13. 在照明系统模拟控制电路实验中，研究人员发现光敏电阻值R（单位：Ω）与光照度E（单位：lx）之间成反比例函数关系，部分数据如下表所示，则光敏电阻值R与光照度E的函数表达式为 ．
光照度E/lx
0.5
1
1.5
2
2.5
3
光敏电阻阻值R/Ω
60
30
20
15
12
10
14. 某水池容积为300m3 ， 原有水100m3 ， 现以xm3／min的速度匀速向水池中注水，注满水需要y min，则y关于x的函数表达式为 ．15. 已知蓄电池的电压为定值，使用蓄电池时，电流I(单位：A)与电阻R(单位： Ω)是反比例函数关系，它的图象如图所示，如果以此蓄电池为电源的用电器，其限制电流不能超过10A，那么用电器可变电阻R应控制的范围是。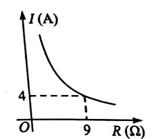
16. 为预防传染病，某校定期对教室进行“药熏消毒”，已知药物燃烧阶段，室内每立方米空气中的含药量y（mg）与燃烧时间x（分钟）成正比例；燃烧后，y与x成反比例（如图所示）．现测得药物10分钟燃烧完，此时教室内每立方米空气含药量为6mg．研究表明当每立方米空气中含药量低于1.2mg时，对人体方能无毒害作用，那么从消毒开始，至少需要经过分钟后，学生才能回到教室．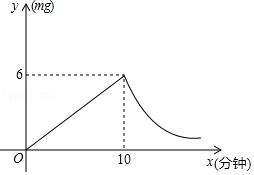
三、综合题
-
17. 张华同学在一次做电学实验时，记录下电流I（安）与电阻R（欧）有如表对应关系：
R
…
2
4
8
10
16
…
I
…
16
8
4
3.2
2
…
通过描点连线，观察并求出I与R之间的函数关系式．
18. 驾驶员血液中每毫升的酒精含量大于或等于200微克即为酒驾，某研究所经实验测得：成人饮用某品牌38度白酒后血液中酒精浓度y（微克/毫升）与饮酒时间x（小时）之间函数关系如图所示（当4≤x≤10时，y与x成反比例）．
(1)、根据图象分别求出血液中酒精浓度上升和下降阶段y与x之间的函数表达式．(2)、问血液中酒精浓度不低于200微克/毫升的持续时间是多少小时？19. 红星粮库需要把晾晒场上的 玉米入库封存，(1)、入库所需的时间 （单位：天）与入库平均速度 （单位： 天）的函数关系是(2)、已知粮库有60名职工晾晒，每天最多可入库300t玉米，预计玉米入库最快可在几天内完成？(3)、60名职工连续工作两天后，天气预报说未来几天会下雨，粮库决定次日把剩下的玉米全部入库，则至少需要增加多少职工？20. 一辆汽车前灯电路上的电压U保持不变，通过调节车灯的电阻值可以改变灯的亮度，下表记录了电流I随电阻R的变化情况：R/Ω
…
2
3
4
5
6
…
I/A
…
6
4
3
2.4
2
…
(1)、求关于R的函数解析式(2)、若车灯通过的最大电流为10A，则车灯电阻的阻值至少是多少?21. 一个蓄水池装满了水，蓄水池的排水速度 是排完水池中的水所用时间 的反比例函数，其图象如图所示.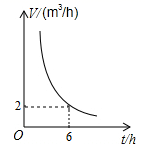
(1)、求出该蓄水池的蓄水量；(2)、若要在 （包括 和 ）将水池的水排完，请求出排水速度的范围.22. 为了预防流感，某校对教室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y（mg0与时间x（min）成正比例，药物燃烧完后，y与x成反比例，现测得药物10（min）燃毕，此时室内空气每立方米的含药量为8mg请根据题中所提供的信息，解答下列问题
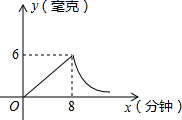(1)、药物燃烧时，y关于x的函数关系式为 ， 自变量x的取值范围是(2)、药物燃烧后，y关于x的函数关系式为(3)、研究表明，当空气中，每立方米的含药量低于1.6mg时，学生方可进教室，那么从消毒开始时，至少需要多少分钟后，学生才能回到教室？23. 某地建设一项水利工程，工程需要运送的土石方总量为360万米 .(1)、写出运输公司完成任务所需的时间y（单位：天）与平均每天的工作量x（单位：万米 ）之间的函数关系式；(2)、当运输公司平均每天的工作量是15万米 时，完成任务所需的时间是多少？24. 教师办公室有一台可以自动加热的饮水机，该饮水机的工作程序是：放满水后，接通电源，则自动开始加热．每分钟水温上升10℃，待加热到100℃时，饮水机自动停止加热，水温开始下降．在水温开始下降的过程中，水温y（℃）和通电时间x（ ）成反比例关系．直至水温降至室温，饮水机再次自动加热，重复上述过程．设某天水温和室温均为20℃，接通电源后，水温y（℃）和通电时间x（ ）之间的关系如图所示，回答下列问题：
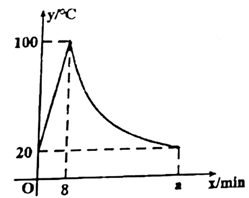(1)、分别求出当 和 时，y和x之间的函数关系式；(2)、求出图中a的值；(3)、李老师这天7：30将饮水机电源打开，若他想在8：10上课前喝到不低于40℃的开水，则他需要在通电多长时间内接水？25. 某项工程需要砂石料 立方米，阳光公司承担了该工程运送砂石料的任务.(1)、在这项任务中平均每天的工作量V(立方米/天)与完成任务所需的时间 (天)之间具有怎样的函数关系?写出这个函数关系式.(2)、阳光公司计划投入A型卡车200辆,每天一共可以运送砂石料2x104立方米,则完成全部运送任务需多少天?(3)、如果工作了25天后,由于工程进度的需要，公司准备再投人A型卡车120辆,在保证每辆车每天工作量不变的前提下，问是否能提前28天完成任务?26. 如图，帆船A和帆船B在太湖湖面上训练，O为湖面上的一个定点，教练船静候于O点，训练时要求A、B两船始终关于O点对称．以O为原点，建立如图所示的坐标系，x轴、y轴的正方向分别表示正东、正北方向．设A、B两船可近似看成在双曲线y＝ 上运动，湖面风平浪静，双帆远影优美，训练中当教练船与A、B两船恰好在直线y＝x上时，三船同时发现湖面上有一遇险的C船，此时教练船测得C船在东南45°方向上，A船测得AC与AB的夹角为60°，B船也同时测得C船的位置（假设C船位置不再改变，A、B、C三船可分别用A、B、C三点表示）．
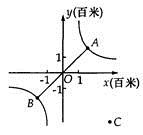(1)、发现C船时，A、B、C三船所在位置的坐标分别为A( ， )、B( ， )和C( ， )；(2)、发现C船，三船立即停止训练，并分别从A、O、B三点出发沿最短路线同时前往救援，设A、B两船的速度相等，教练船与A船的速度之比为3：4，问教练船是否最先赶到？请说明理由．