备考2022年中考数学一轮复习(湘教版)专题30 反比例函数及其图像与性质
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
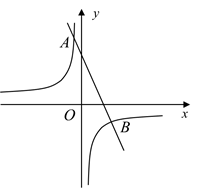
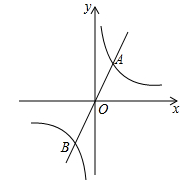
1. 已知反比例函数 的图象与正比例函数 的图象相交于 两点,若点 的坐标是 ,则点 的坐标是( )A、 B、 C、 D、2. 一次函数 的图象与x轴交于点B,与反比例函数 的图象交于点 ,且 的面积为1,则m的值是( )A、1 B、2 C、3 D、43. 根据反比例函数的性质、联系化学学科中的溶质质量分数的求法以及生活体验等,判定下列有关函数 (a为常数且 )的性质表述中,正确的是( )
①y随x的增大而增大;②y随x的增大而减小;③ ;④
A、①③ B、①④ C、②③ D、②④4. 一次函数 与反比例函数 的图象交于点 ,点 .当 时,x的取值范围是( )A、 B、 或 C、 D、 或5. 已知点 , 都在反比例函数 的图象上,且 ,则 , 的关系是( )A、 B、 C、 D、6. 如图,O是坐标原点,点B在x轴上,在 OAB中,AO=AB=5,OB=6,点A在反比例函数y= (k≠0)图象上,则k的值( ) A、﹣12 B、﹣15 C、﹣20 D、﹣307. 已知双曲线 过点(3, )、(1, )、(-2, ),则下列结论正确的是( )A、 B、 C、 D、8. 如图,点A在曲线到 上,点B在双曲线 上, 轴,点C是x轴上一点,连接 、 ,若 的面积是6,则k的值( )
A、﹣12 B、﹣15 C、﹣20 D、﹣307. 已知双曲线 过点(3, )、(1, )、(-2, ),则下列结论正确的是( )A、 B、 C、 D、8. 如图,点A在曲线到 上,点B在双曲线 上, 轴,点C是x轴上一点,连接 、 ,若 的面积是6,则k的值( )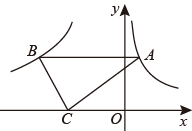 A、-6 B、-8 C、-10 D、-129. 在反比例函数 ( 为常数)上有三点 , , ,若 ,则 , , 的大小关系为( )A、 B、 C、 D、10. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、
A、-6 B、-8 C、-10 D、-129. 在反比例函数 ( 为常数)上有三点 , , ,若 ,则 , , 的大小关系为( )A、 B、 C、 D、10. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、二、填空题
-
11. 请写出一个图象在第二、四象限的反比例函数的表达式:.12. 在反比例函数y= 的图象的每一支曲线上,函数值y随自变量x的增大而增大,则m的取值范围是 .13. 如图,矩形 的顶点 在反比例函数 的图象上,矩形 的面积为3,则 ;
 14. 如图,点 在反比例函数 的图象上,点M在x轴的正半轴上,点N在y轴的负半轴上,且 .点 是线段 上一动点,过点A和P分别作x轴的垂线,垂足为点D和E,连接 、 .当 时,x的取值范围是.
14. 如图,点 在反比例函数 的图象上,点M在x轴的正半轴上,点N在y轴的负半轴上,且 .点 是线段 上一动点,过点A和P分别作x轴的垂线,垂足为点D和E,连接 、 .当 时,x的取值范围是. 15. 如图,点A、B在反比例函数 的图象上,延长AB交x轴于C点,若△AOC的面积是12,且点B是AC的中点,则 =.
15. 如图,点A、B在反比例函数 的图象上,延长AB交x轴于C点,若△AOC的面积是12,且点B是AC的中点,则 =. 16. 若 , 是反比例函数 图象上的两点,则 、 的大小关系是 (填“>”、“=”或“<”)17. 已知点 , 为反比例函数 图象上的两点,则 与 的大小关系是 .(填“>”“=”或“<”)18. 若点 , 在反比例函 的图象上,则 (填“>“<”或“=”).19. 点 、 是反比例函数 图象上的两点,满足:当 时,均有 ,则 的取值范围是.20. 已知点 , 在反比例函数 ( 是常数)的图象上,且 ,则 的取值范围是.
16. 若 , 是反比例函数 图象上的两点,则 、 的大小关系是 (填“>”、“=”或“<”)17. 已知点 , 为反比例函数 图象上的两点,则 与 的大小关系是 .(填“>”“=”或“<”)18. 若点 , 在反比例函 的图象上,则 (填“>“<”或“=”).19. 点 、 是反比例函数 图象上的两点,满足:当 时,均有 ,则 的取值范围是.20. 已知点 , 在反比例函数 ( 是常数)的图象上,且 ,则 的取值范围是.三、解答题
-
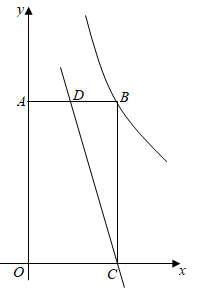
21. 如图,在平面直角坐标系中.四边形 为矩形,点 、 分别在 轴和 轴的正半轴上,点 为 的中点已知实数 ,一次函数 的图象经过点 、 ,反比例函数 的图象经过点 ,求 的值.
 22. 如图,点A是反比例函数y=图象上的一点,过点A作AB⊥x轴于点B,连接OA,若△OAB的面积为2,求该反比例函数的解析式.
22. 如图,点A是反比例函数y=图象上的一点,过点A作AB⊥x轴于点B,连接OA,若△OAB的面积为2,求该反比例函数的解析式. 23. 已知x1 , x2 , x3是y= 图像上三个点的横坐标,且满足x3>x2>x1>0。请比较 与 的大小,并说明理由。
23. 已知x1 , x2 , x3是y= 图像上三个点的横坐标,且满足x3>x2>x1>0。请比较 与 的大小,并说明理由。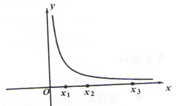 24. 已知y﹣1与x成反比例,当x=1时,y=﹣5,求y与x的函数表达式.25. 反比例函数 与 在第一象限内的图象如图所示,过x轴上点A作y轴的平行线,与函数 , 的图象交点依次为P、Q两点.若PQ=2,求PA的长.
24. 已知y﹣1与x成反比例,当x=1时,y=﹣5,求y与x的函数表达式.25. 反比例函数 与 在第一象限内的图象如图所示,过x轴上点A作y轴的平行线,与函数 , 的图象交点依次为P、Q两点.若PQ=2,求PA的长.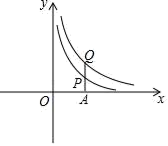 26. 如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A、B,与反比例函数 的图象在第四象限交于点C,CD⊥x轴于点D,tan∠OAB=2,OA=2,OD=1.
26. 如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A、B,与反比例函数 的图象在第四象限交于点C,CD⊥x轴于点D,tan∠OAB=2,OA=2,OD=1. (1)、求该反比例函数的表达式;(2)、点M是这个反比例函数图象上的点,过点M作MN⊥y轴,垂足为点N,连接OM、AN,如果S△ABN=2S△OMN , 直接写出点M的坐标.
(1)、求该反比例函数的表达式;(2)、点M是这个反比例函数图象上的点,过点M作MN⊥y轴,垂足为点N,连接OM、AN,如果S△ABN=2S△OMN , 直接写出点M的坐标.四、综合题
-
27. 如图,已知在平面直角坐标系 中,正比例函数 的图象与反比例函数 的图象有一个交点 .
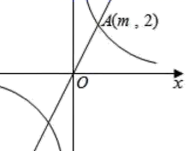 (1)、 求的值;(2)、试判断点 是否在反比例函数图象上,并说明理由.28. 小欣在学习了反比例函数的图象与性质后,进一步研究了函数 的图象与性质.其研究过程如下:(1)、绘制函数图象
(1)、 求的值;(2)、试判断点 是否在反比例函数图象上,并说明理由.28. 小欣在学习了反比例函数的图象与性质后,进一步研究了函数 的图象与性质.其研究过程如下:(1)、绘制函数图象①列表:下表是 与 的几组对应值,其中 ▲ ;
…
-4
-3
-2
0
1
2
…
…
-1
=2
-3
3
2
…
②描点:根据表中的数值描点 ,请补充描出点 ;
③连线:用平滑的曲线顺次连接各点,请把图象补充完整.
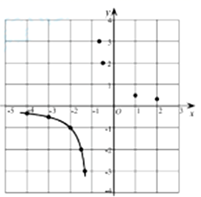 (2)、探究函数性质
(2)、探究函数性质判断下列说法是否正确。
①函数值 随 的增大而减小:
②函数图象关于原点对称:
③函数图象与直线 没有交点.
29. 如图,大、小两个正方形的中心均与平面直角坐标系的原点O重合,边分别与坐标轴平行,反比例函数 的图象与大正方形的一边交于点A(1,2),且经过小正方形的顶点B. (1)、求反比例函数的解析式;(2)、求图中阴影部分的面积.30. 如图,直线 交 轴于点M , 四边形OMAE是矩形,S矩形OMAE=4,反比例函数 的图象经过点A , EA的延长线交直线 于点D .
(1)、求反比例函数的解析式;(2)、求图中阴影部分的面积.30. 如图,直线 交 轴于点M , 四边形OMAE是矩形,S矩形OMAE=4,反比例函数 的图象经过点A , EA的延长线交直线 于点D .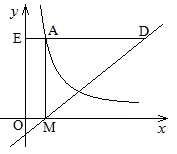 (1)、求反比例函数的解析式;(2)、若点B在 轴上,且AB=AD , 求点B的坐标.
(1)、求反比例函数的解析式;(2)、若点B在 轴上,且AB=AD , 求点B的坐标.