备考2022年中考数学一轮复习(湘教版)专题26 函数和它的表示法
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
1. 一对变量满足如图的函数关系.设计以下问题情境:
①小明从家骑车以600米/分的速度匀速骑了2.5分钟,在原地停留了2分钟,然后以1000米/分的速度匀速骑回家.设所用时间为x分钟;②有一个容积为1.5升的开口空瓶,小张以0.6升/秒的速度匀速向这个空瓶注水,注满后停止,再以1升/秒的速度匀速倒空瓶中的水.设所用时间为x秒,瓶内水的体积为y升;③在矩形ABCD中,AB=2,BC=1.5,△ABP的面积为y.其中,符合图中函数关系的情境个数为( )
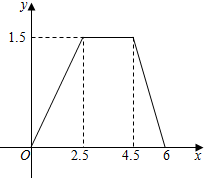 A、3 B、2 C、1 D、02. 如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是( )
A、3 B、2 C、1 D、02. 如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是( )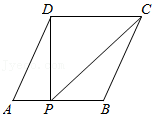 A、
A、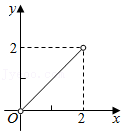 B、
B、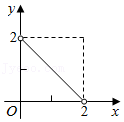 C、
C、 D、
D、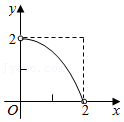 3. 为规范市场秩序、保障民生工程,监管部门对某一商品的价格持续监控.该商品的价格 (元/件)随时间t(天)的变化如图所示,设 (元/件)表示从第1天到第t天该商品的平均价格,则 随t变化的图象大致是( )
3. 为规范市场秩序、保障民生工程,监管部门对某一商品的价格持续监控.该商品的价格 (元/件)随时间t(天)的变化如图所示,设 (元/件)表示从第1天到第t天该商品的平均价格,则 随t变化的图象大致是( )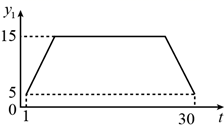 A、
A、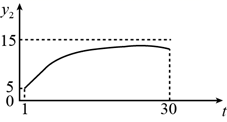 B、
B、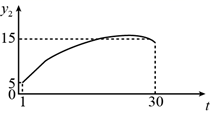 C、
C、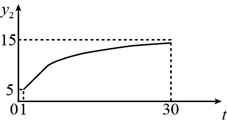 D、
D、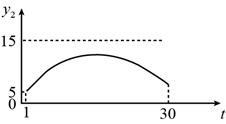 4. 函数 的自变量 的取值范围是( )A、 B、 C、 且 D、 且5. 如图1,矩形 中,点 为 的中点,点 沿 从点 运动到点 ,设 , 两点间的距离为 , ,图2是点 运动时 随 变化的关系图象,则 的长为( )
4. 函数 的自变量 的取值范围是( )A、 B、 C、 且 D、 且5. 如图1,矩形 中,点 为 的中点,点 沿 从点 运动到点 ,设 , 两点间的距离为 , ,图2是点 运动时 随 变化的关系图象,则 的长为( )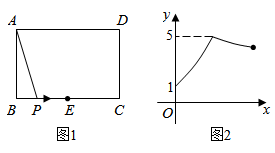 A、4 B、5 C、6 D、76. 如图,在正方形ABCD中,AB=4,动点M从点A出发,以每秒1个单位长度的速度沿射线AB运动,同时动点N从点A出发,以每秒2个单位长度的速度沿折线AD→DC→CB运动,当点N运动到点B时,点M , N同时停止运动.设 AMN的面积为y , 运动时间为x(s),则下列图象能大致反映y与x之间函数关系的是( )
A、4 B、5 C、6 D、76. 如图,在正方形ABCD中,AB=4,动点M从点A出发,以每秒1个单位长度的速度沿射线AB运动,同时动点N从点A出发,以每秒2个单位长度的速度沿折线AD→DC→CB运动,当点N运动到点B时,点M , N同时停止运动.设 AMN的面积为y , 运动时间为x(s),则下列图象能大致反映y与x之间函数关系的是( ) A、
A、 B、
B、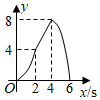 C、
C、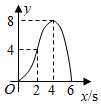 D、
D、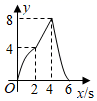 7. 某天早晨7:00,小明从家骑自行车去上学,途中因自行车发生故障,就地修车耽误了一段时间,修好车后继续骑行,7:30赶到了学校.图所示的函数图象反映了他骑车上学的整个过程.结合图象,判断下列结论正确的是( )
7. 某天早晨7:00,小明从家骑自行车去上学,途中因自行车发生故障,就地修车耽误了一段时间,修好车后继续骑行,7:30赶到了学校.图所示的函数图象反映了他骑车上学的整个过程.结合图象,判断下列结论正确的是( )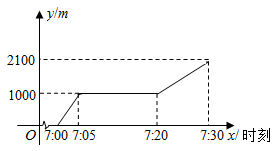 A、小明修车花了15min B、小明家距离学校1100m C、小明修好车后花了30min到达学校 D、小明修好车后骑行到学校的平均速度是3m/s8. 甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中甲、乙两人之间的距离 (米)与乙出发的时间x(秒)之间的函数关系如图所示,正确的个数为( )
A、小明修车花了15min B、小明家距离学校1100m C、小明修好车后花了30min到达学校 D、小明修好车后骑行到学校的平均速度是3m/s8. 甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中甲、乙两人之间的距离 (米)与乙出发的时间x(秒)之间的函数关系如图所示,正确的个数为( )①乙的速度为5米/秒;②离开起点后,甲、乙两人第一次相遇时,距离起点12米;③甲、乙两人之间的距离超过32米的时间范围是 ;④乙到达终点时,甲距离终点还有68米.
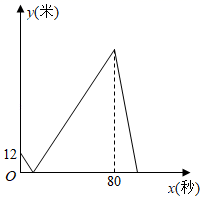 A、4 B、3 C、2 D、19. 小明从家出发沿笔直的公路去图书馆,在图书馆阅读书报后按原路回到家.如图,反映了小明离家的距离y(单位:km)与时间t(单位:h)之间的对应关系.下列描述错误的是( )
A、4 B、3 C、2 D、19. 小明从家出发沿笔直的公路去图书馆,在图书馆阅读书报后按原路回到家.如图,反映了小明离家的距离y(单位:km)与时间t(单位:h)之间的对应关系.下列描述错误的是( )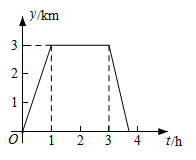 A、小明家距图书馆3km B、小明在图书馆阅读时间为2h C、小明在图书馆阅读书报和往返总时间不足4h D、小明去图书馆的速度比回家时的速度快10. 如图,在矩形 中, , ,动点P沿折线 运动到点B , 同时动点Q沿折线 运动到点C , 点 在矩形边上的运动速度为每秒1个单位长度,点P , Q在矩形对角线上的运动速度为每秒2个单位长度.设运动时间为t秒, 的面积为S , 则下列图象能大致反映S与t之间函数关系的是( )
A、小明家距图书馆3km B、小明在图书馆阅读时间为2h C、小明在图书馆阅读书报和往返总时间不足4h D、小明去图书馆的速度比回家时的速度快10. 如图,在矩形 中, , ,动点P沿折线 运动到点B , 同时动点Q沿折线 运动到点C , 点 在矩形边上的运动速度为每秒1个单位长度,点P , Q在矩形对角线上的运动速度为每秒2个单位长度.设运动时间为t秒, 的面积为S , 则下列图象能大致反映S与t之间函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、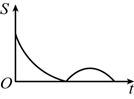
二、填空题
-
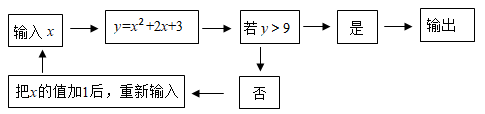
11. 已知函数y= ,若y=2,则x=.12. 如图所示:是一个运算程序示意图,若第一次输入1,则输出的结果是;
 13. 春耕期间,市农资公司连续8天调进一批化肥,并在开始调进化肥的第七天开始销售.若进货期间每天调进化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个公司的化肥存量s(单位:吨)与时间t(单位:天)之间的函数关系如图所示,则该公司这次化肥销售活动(从开始进货到销售完毕)所用的时间是天.
13. 春耕期间,市农资公司连续8天调进一批化肥,并在开始调进化肥的第七天开始销售.若进货期间每天调进化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个公司的化肥存量s(单位:吨)与时间t(单位:天)之间的函数关系如图所示,则该公司这次化肥销售活动(从开始进货到销售完毕)所用的时间是天.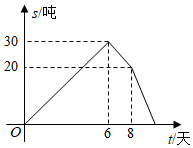 14. 如图(1),在 中, , ,边 上的点 从顶点 出发,向顶点 运动,同时,边 上的点 从顶点 出发,向顶点 运动, , 两点运动速度的大小相等,设 , , 关于 的函数图象如图(2),图象过点 ,则图象最低点的横坐标是.
14. 如图(1),在 中, , ,边 上的点 从顶点 出发,向顶点 运动,同时,边 上的点 从顶点 出发,向顶点 运动, , 两点运动速度的大小相等,设 , , 关于 的函数图象如图(2),图象过点 ,则图象最低点的横坐标是.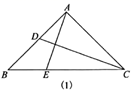
 15. 甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
15. 甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:甲:函数的图象经过点(0,1);
乙:y随x的增大而减小;
丙:函数的图象不经过第三象限.
根据他们的叙述,写出满足上述性质的一个函数表达式为 .
16. 已知甲乙两车分别从A、B两地出发,相向匀速行驶,已知乙车先出发,1小时后甲车再出发.一段时间后,甲乙两车在休息站C地相遇:到达C地后,乙车不休息继续按原速前往A地,甲车休息半小时后再按原速前往B地,甲车到达B地停止运动;乙车到A地后立刻原速返回B地,已知两车间的距离y(km)随乙车运动的时间x(h)变化如图,则当甲车到达B地时,乙车距离B地的距离为(km).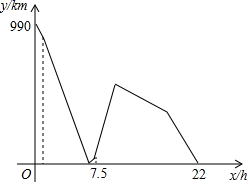
三、作图题
-
17. 用描点法画函数 的图象.
x
...
-3
-2
-1
0
1
2
3
...
y
...
四、解答题
-
18.
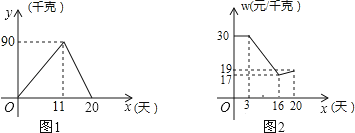
小明家今年种植的草莓喜获丰收,采摘上市20天全部销售完,爸爸让他对今年的销售情况进行跟踪记录,小明利用所学的数学知识将记录情况绘成图象(所得图象均为线段),日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,草莓的价格w(单位:元/千克)与上市时间x(单位:天)的函数关系如图2所示.
(1)观察图象,直接写出当0≤x≤11时,日销售量y与上市时间x之间的函数解析式为 ;当11≤x≤20时,日销售量y与上市时间x之间的函数解析式为 .
(2)试求出第11天的销售金额;
(3)若上市第15天时,爸爸把当天能销售的草莓批发给了邻居马叔叔,批发价为每千克15元,马叔叔到市场按照当日的价格w元/千克将批发来的草莓全部销售完,他在销售的过程中,草莓总质量损耗了2%.那么,马叔叔支付完来回车费20元后,当天能赚到多少元?
 19. 在同一直角坐标系xOy内,作出二次函数y=x2和y=x2+1的草图,这两个函数的图象间有什么联系?
19. 在同一直角坐标系xOy内,作出二次函数y=x2和y=x2+1的草图,这两个函数的图象间有什么联系? 20. 正方形的边长是 2cm,设它的边长增加 x cm时,正方形的面积增加 y cm2,求y与x之间的函数关系.21. 函数常用的表示方法有三种.
20. 正方形的边长是 2cm,设它的边长增加 x cm时,正方形的面积增加 y cm2,求y与x之间的函数关系.21. 函数常用的表示方法有三种.
已知A、B两地相距30千米,小王以40千米/时的速度骑摩托车从A地出发匀速前往B地参加活动.请选择两种方法来表示小王与B地的距离y(千米)与行驶时间x(小时)之间的函数关系.
22.游泳池常需进行换水清洗,图中的折线表示的是游泳池换水清洗过程“排水——清洗——灌水”中水量y(m3)与时间t(min)之间的函数关系式.
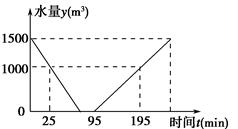
(1)根据图中提供的信息,求整个换水清洗过程水量y(m3)与时间t(min)的函数解析式;
(2)问:排水、清洗、灌水各花多少时间?23. 已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.x
…
1
2
4
5
6
8
9
…
y
…
3.92
1.95
0.98
0.78
2.44
2.44
0.78
…
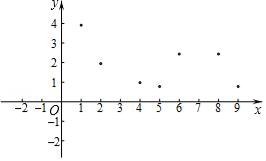
小风根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象和性质进行了探究.
下面是小风的探究过程,请补充完整:
(1)、如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(2)、根据画出的函数图象,写出:①x=7对应的函数值y约为多少;
②写出该函数的一条性质.
 24.
24.某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示:根据图象解答下列问题:
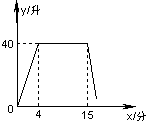 (1)、洗衣机的进水时间是分钟;清洗时洗衣机中的水量是升;(2)、已知洗衣机的排水速度为每分钟19升,
(1)、洗衣机的进水时间是分钟;清洗时洗衣机中的水量是升;(2)、已知洗衣机的排水速度为每分钟19升,①求排水时y与x之间的关系式.
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量.
五、综合题
-
25. 一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,两车在途中相遇时,快车恰巧出现故障,慢车继续驶往甲地,快车维修好后按原速继续行驶乙地,两车到达各地终点后停止,两车之间的距离s(km)与慢车行驶的时间t(h)之间的关系如图:
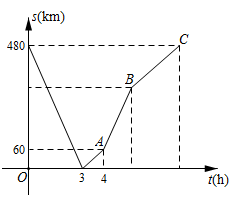 (1)、快车的速度为km/h,C点的坐标为.(2)、慢车出发多少小时候,两车相距200km.26. 根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米~80米为“中途期”,80米~100米为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度y(m/s)与路程x(m)之间的观测数据,绘制成曲线如图所示.
(1)、快车的速度为km/h,C点的坐标为.(2)、慢车出发多少小时候,两车相距200km.26. 根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米~80米为“中途期”,80米~100米为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度y(m/s)与路程x(m)之间的观测数据,绘制成曲线如图所示.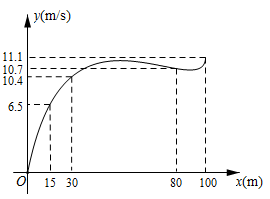 (1)、y是关于x的函数吗?为什么?(2)、“加速期”结束时,小斌的速度为多少?(3)、根据如图提供的信息,给小斌提一条训练建议.27. 小明根据学习函数的经验,参照研究函数的过程与方法,对函数 的图象与性质进行探究.
(1)、y是关于x的函数吗?为什么?(2)、“加速期”结束时,小斌的速度为多少?(3)、根据如图提供的信息,给小斌提一条训练建议.27. 小明根据学习函数的经验,参照研究函数的过程与方法,对函数 的图象与性质进行探究.因为 ,即 ,所以可以对比函数 来探究.
(1)、观察图象并分析表格,回答下列问题:①当 时, 随 的增大而;(填“增大”或“减小”)
②函数 的图象是由 的图象向 平移 个单位而得到.
③函数图象关于点 中心对称.(填点的坐标)
(2)、列表:
下表列出 与 的几组对应值,请写出 , 的值: , ;…
-4
-3
-2
-1
1
2
3
4
…
…
1
2
4
-4
-2
-1
…
…
2
3
-3
-1
0
…
(3)、描点:在平面直角坐标系中,以自变量 的取值为横坐标,以 相应的函数值为纵坐标,描出相应的点,如图所示:
请把 轴左边各点和右边各点,分别用条光滑曲线顺次连接起来:
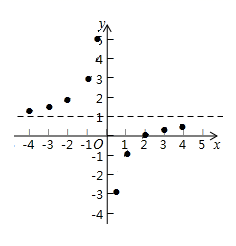 28. 已知函数(1)、画出函数图象;
28. 已知函数(1)、画出函数图象;列表:
x
. ..
. ..
y
. ..
. ..
描点,连线得到函数图象:
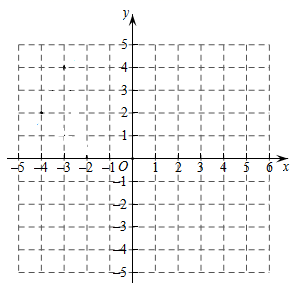 (2)、该函数是否有最大或最小值?若有,求出其值,若没有,简述理由;(3)、设 是函数图象上的点,若 ,证明: .29. 小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟.在此过程中,设妈妈从商店出发开始所用时间为t(分钟),图1表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象;图2中线段 表示小华和商店的距离 (米)与时间t(分钟)的函数关系的图象的一部分,请根据所给信息解答下列问题:
(2)、该函数是否有最大或最小值?若有,求出其值,若没有,简述理由;(3)、设 是函数图象上的点,若 ,证明: .29. 小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟.在此过程中,设妈妈从商店出发开始所用时间为t(分钟),图1表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象;图2中线段 表示小华和商店的距离 (米)与时间t(分钟)的函数关系的图象的一部分,请根据所给信息解答下列问题: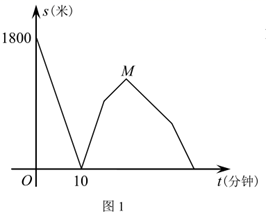
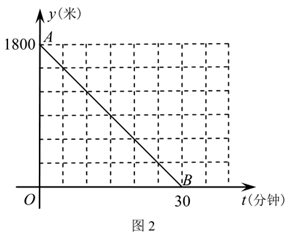 (1)、填空:妈妈骑车的速度是米/分钟,妈妈在家装载货物所用时间是分钟,点M的坐标是;(2)、直接写出妈妈和商店的距离 (米)与时间t(分钟)的函数关系式,并在图2中画出其函数图象;(3)、求t为何值时,两人相距360米.30. 通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量x与函数值y的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
(1)、填空:妈妈骑车的速度是米/分钟,妈妈在家装载货物所用时间是分钟,点M的坐标是;(2)、直接写出妈妈和商店的距离 (米)与时间t(分钟)的函数关系式,并在图2中画出其函数图象;(3)、求t为何值时,两人相距360米.30. 通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量x与函数值y的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:…
0
1
2
3
4
5
…
…
6
3
2
1.5
1.2
1
…
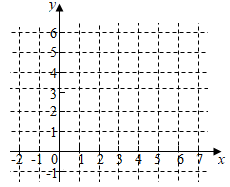 (1)、当 时, ;(2)、根据表中数值描点 ,并画出函数图象;(3)、观察画出的图象,写出这个函数的一条性质:.31. 随着 技术的发展,人们对各类 产品的使用充满期待.某公司计划在某地区销售第一款 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第 ( 为正整数)个销售周期每台的销售价格为 元, 与 之间满足如图所示的一次函数关系.
(1)、当 时, ;(2)、根据表中数值描点 ,并画出函数图象;(3)、观察画出的图象,写出这个函数的一条性质:.31. 随着 技术的发展,人们对各类 产品的使用充满期待.某公司计划在某地区销售第一款 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第 ( 为正整数)个销售周期每台的销售价格为 元, 与 之间满足如图所示的一次函数关系.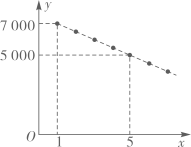 (1)、求 与 之间的关系式;(2)、设该产品在第 个销售周期的销售数量为 (万台), 与 的关系可用 来描述。根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?32. 若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数 的图象与性质.列表:
(1)、求 与 之间的关系式;(2)、设该产品在第 个销售周期的销售数量为 (万台), 与 的关系可用 来描述。根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?32. 若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数 的图象与性质.列表:x
…
0
1
2
3
…
y
…
1
2
1
0
1
2
…
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
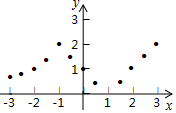 (1)、如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;(2)、研究函数并结合图象与表格,回答下列问题:
(1)、如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;(2)、研究函数并结合图象与表格,回答下列问题:①点 , , , 在函数图象上, , ;(填“>”,“=”或“<”)
②当函数值 时,求自变量x的值;
③在直线 的右侧的函数图象上有两个不同的点 , ,且 ,求 的值;
④若直线 与函数图象有三个不同的交点,求a的取值范围.
33. 国家创新指数是反映一个国家科学技术和创新竞争力的综合指数.对国家创新指数得分排名前40的国家的有关数据进行收集、整理、描述和分析.下面给出了部分信息:a.国家创新指数得分的频数分布直方图(数据分成7组:
30≤x<40,40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);

b.国家创新指数得分在60≤x<70这一组的是:61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5
c.40个国家的人均国内生产总值和国家创新指数得分情况统计图:
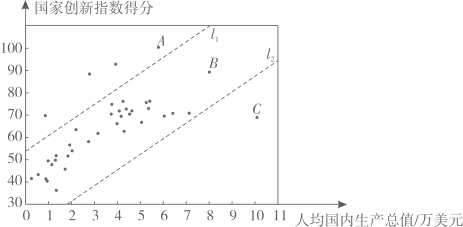
d.中国的国家创新指数得分为69.5.
(以上数据来源于《国家创新指数报告(2018)》)
根据以上信息,回答下列问题:
(1)、中国的国家创新指数得分排名世界第;(2)、在40个国家的人均国内生产总值和国家创新指数得分情况统计图中,包括中国在内的少数几个国家所对应的点位于虚线 的上方.请在图中用“ ”圈出代表中国的点;(3)、在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为万美元;(结果保留一位小数)(4)、下列推断合理的是 .①相比于点A,B所代表的国家,中国的国家创新指数得分还有一定差距,中国提出“加快建设创新型国家”的战略任务,进一步提高国家综合创新能力;
②相比于点B,C所代表的国家,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
34. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃停止加热,水温开始下降,此时水温 (℃)与开机后用时 ( )成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温 (℃)与时间 ( )的关系如图所示: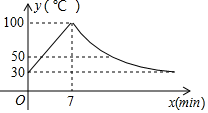 (1)、分别写出水温上升和下降阶段 与 之间的函数关系式;(2)、怡萱同学想喝高于50℃的水,请问她最多需要等待多长时间?
(1)、分别写出水温上升和下降阶段 与 之间的函数关系式;(2)、怡萱同学想喝高于50℃的水,请问她最多需要等待多长时间?
-