备考2022年中考数学一轮复习(湘教版)专题25 平面直角坐标系
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
1. 数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如a+bi(a,b为实数)的数叫做复数,用z=a+bi表示,任何一个复数z=a+bi在平面直角坐标系中都可以用有序数对Z(a,b)表示,如:z=1+2i表示为Z(1,2),则z=2﹣i可表示为( )A、Z(2,0) B、Z(2,﹣1) C、Z(2,1) D、Z(﹣1,2)2. 如图,若在象棋盘上建立直角坐标系,使“帅”位于点(﹣1,﹣2).“馬”位于点(2,﹣2),则“兵”位于点( )
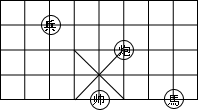 A、(﹣1,1) B、(﹣2,﹣1) C、(﹣3,1) D、(1,﹣2)3. 在平面直角坐标系中,将点P(3,2)向上平移2个单位长度,得到的点的坐标是( )A、(3,4) B、(1,2) C、(5,2) D、(3 ,0)4. 将点 沿x轴向左平移3个单位长度后得到的点 的坐标为( )A、 B、 C、 D、5. 在平面直角坐标系中,将点A(-1,2)向下平移3个单位长度,再向右平移2个单位长度,得到点A′,则点A′的坐标是( )A、(-3,-1) B、(1,-1) C、(-1,1) D、(-4,4)6. 在平面直角坐标系中,点 在第三象限内,则a的取值范围是( )A、 B、 C、 D、7. 已知平面直角坐标系中点 .将它沿 轴方向向上平移3个单位所得点的坐标是( )A、 B、 C、 D、8. 已知点 关于原点对称的点在第二象限,则a的取值范围在数轴上表示( )A、
A、(﹣1,1) B、(﹣2,﹣1) C、(﹣3,1) D、(1,﹣2)3. 在平面直角坐标系中,将点P(3,2)向上平移2个单位长度,得到的点的坐标是( )A、(3,4) B、(1,2) C、(5,2) D、(3 ,0)4. 将点 沿x轴向左平移3个单位长度后得到的点 的坐标为( )A、 B、 C、 D、5. 在平面直角坐标系中,将点A(-1,2)向下平移3个单位长度,再向右平移2个单位长度,得到点A′,则点A′的坐标是( )A、(-3,-1) B、(1,-1) C、(-1,1) D、(-4,4)6. 在平面直角坐标系中,点 在第三象限内,则a的取值范围是( )A、 B、 C、 D、7. 已知平面直角坐标系中点 .将它沿 轴方向向上平移3个单位所得点的坐标是( )A、 B、 C、 D、8. 已知点 关于原点对称的点在第二象限,则a的取值范围在数轴上表示( )A、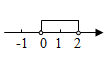 B、
B、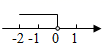 C、
C、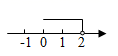 D、
D、 9. 下图是利用平面直角坐标系画出的首钢园中部分场馆建筑的分布图,若这个坐标系分别以正东、正北方向为 轴、 轴的正方向,表示群明湖的点的坐标为 ,表示冰壶馆的点的坐标为 ,则表示下列场馆建筑的点的坐标正确的是( )
9. 下图是利用平面直角坐标系画出的首钢园中部分场馆建筑的分布图,若这个坐标系分别以正东、正北方向为 轴、 轴的正方向,表示群明湖的点的坐标为 ,表示冰壶馆的点的坐标为 ,则表示下列场馆建筑的点的坐标正确的是( ) A、滑雪大跳台 B、五一剧场 C、冬奥组委会 D、全民畅读艺术书店10. 已知点P(2,a-1)到两坐标轴的距离相等,则a的值为( )A、3 B、-3或1 C、-1 D、3或-1
A、滑雪大跳台 B、五一剧场 C、冬奥组委会 D、全民畅读艺术书店10. 已知点P(2,a-1)到两坐标轴的距离相等,则a的值为( )A、3 B、-3或1 C、-1 D、3或-1二、填空题
-
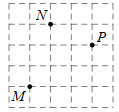
11. 已知点 在第一象限,到x轴的距离为2,则m= .12. 如图,某小区有古树 棵,分别记作为 若建立平面直角坐标系,将古树 用坐标分别表示为 和 ,则古树 用坐标表示为
 13. 若点P在函数 的图象上,且到x轴的距离等于1,则点P的坐标是 .14. 2020年10月23日在北京人民大会堂隆重举行了纪念中国人民志愿军抗美援朝出国作战70周年大会.在伟大的抗美援朝战争中,上甘岭战役是一场惨烈空前的战役.下图是利用网格画出的上甘岭战役的示意图.若建立适当的平面直角坐标系,表示上所里的点的坐标为(-1,2),表示注字洞的点的坐标为(0,3),则表示上甘岭的点(正好在网格点上)的坐标为 .
13. 若点P在函数 的图象上,且到x轴的距离等于1,则点P的坐标是 .14. 2020年10月23日在北京人民大会堂隆重举行了纪念中国人民志愿军抗美援朝出国作战70周年大会.在伟大的抗美援朝战争中,上甘岭战役是一场惨烈空前的战役.下图是利用网格画出的上甘岭战役的示意图.若建立适当的平面直角坐标系,表示上所里的点的坐标为(-1,2),表示注字洞的点的坐标为(0,3),则表示上甘岭的点(正好在网格点上)的坐标为 . 15. 如图是房山区行政规划图.如果周口店的坐标是(-2,1),阎村的坐标是(0,2),那么燕山的坐标是 , 窦店坐标是 .
15. 如图是房山区行政规划图.如果周口店的坐标是(-2,1),阎村的坐标是(0,2),那么燕山的坐标是 , 窦店坐标是 . 16. 在平面直角坐标系中,线段 在 轴上, ,且点 ,则点 的坐标是 .17. 在平面直角坐标系中,点P( ,﹣3)在第象限.18. 矩形ABCD中,A(﹣3,2),B(0,2),C(0,3),则点D坐标为.
16. 在平面直角坐标系中,线段 在 轴上, ,且点 ,则点 的坐标是 .17. 在平面直角坐标系中,点P( ,﹣3)在第象限.18. 矩形ABCD中,A(﹣3,2),B(0,2),C(0,3),则点D坐标为.三、解答题
-
19. 已知点P(2m+4,m﹣1).试分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3;
(2)点P在过A(2,﹣3)点,且与x轴平行的直线上.
20. 已知三角形ABC的两个顶点坐标为A(﹣4,0),B(2,0),如图,且过这两个点的边上的高为4,第三个顶点的横坐标为﹣1,求顶点C的坐标及三角形的面积. 21. 已知点A(1+2a,4a﹣5),且点A到两坐标轴的距离相等,求点A的坐标.22.
21. 已知点A(1+2a,4a﹣5),且点A到两坐标轴的距离相等,求点A的坐标.22.如图,一点光源在(0,3)处,沿所示的方向发射,长方形四条边上有四个平面镜,与坐标平面垂直放置,设第一个入射点P1坐标为(3,0),则第二个入射点P2( , ),第三个入射点P3( , ),作出光路图,并写出第2013个入射点P2013( , )
 23.
23.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.
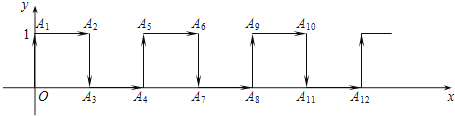
(1)填写下列各点的坐标:A4( , ),A8( , ),A12( , ).
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A100到点A101的移动方向.
24.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.
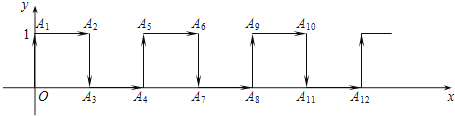
(1)填写下列各点的坐标:A4( , ),A8( , ),A12( , );
(2)写出点A4n的坐标(n是正整数)( , );
(3)指出蚂蚁从点A2014到点A2015的移动方向为 .
25. 在平面直角坐标系中,点A(a,3﹣2a)在第一象限.(1)若点A到x轴的距离与到y轴的距离相等,求a的值;
(2)若点A到x轴的距离小于到y轴的距离,求a的取值范围.
26. 在平面直角坐标系,点P(3n+2,4﹣2n)在第四象限,求实数n的取值范围.27. 如果B(m+1,3m﹣5)到x轴的距离与它到y轴的距离相等,求m.28. 在平面直角坐标系中,点A的坐标是(3a﹣5,a+1)(1)若点A在y轴上,求a的值及点A的坐标.
(2)若点A到x轴的距离与到y轴的距离相等;求a的值及点A的坐标.
四、综合题
-
29. 在平面直角坐标系中,若点P(x,y)的坐标x、y均为整数,则称点P为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
 (1)、求出图中格点四边形DEFG对应的S,N,L的值.(2)、已知格点多边形的面积可表示为S=N+aL+b,其中a,b为常数,若某格点多边形对应的N=82,L=38,求S的值.30. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
(1)、求出图中格点四边形DEFG对应的S,N,L的值.(2)、已知格点多边形的面积可表示为S=N+aL+b,其中a,b为常数,若某格点多边形对应的N=82,L=38,求S的值.30. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.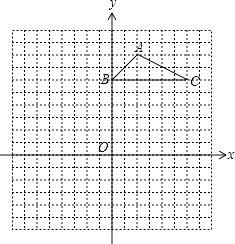 (1)、点A的坐标为 , 点C的坐标为 .(2)、将△ABC向左平移7个单位,请画出平移后的△A1B1C1 . 若M为△ABC内的一点,其坐标为(a,b),则平移后点M的对应点M1的坐标为 .(3)、以原点O为位似中心,将△ABC缩小,使变换后得到的△A2B2C2与△ABC对应边的比为1:2.请在网格内画出△A2B2C2 , 并写出点A2的坐标: .31. 如图,已知△ABC的三个顶点坐标为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)、点A的坐标为 , 点C的坐标为 .(2)、将△ABC向左平移7个单位,请画出平移后的△A1B1C1 . 若M为△ABC内的一点,其坐标为(a,b),则平移后点M的对应点M1的坐标为 .(3)、以原点O为位似中心,将△ABC缩小,使变换后得到的△A2B2C2与△ABC对应边的比为1:2.请在网格内画出△A2B2C2 , 并写出点A2的坐标: .31. 如图,已知△ABC的三个顶点坐标为A(﹣2,3),B(﹣6,0),C(﹣1,0). (1)、将△ABC绕坐标原点O旋转180°,画出图形,并写出点A的对应点P的坐标 .(2)、将△ABC绕坐标原点O逆时针旋转90°,直接写出点A的对应点Q的坐标 .(3)、请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标 .32. 如图是游乐园的一角.
(1)、将△ABC绕坐标原点O旋转180°,画出图形,并写出点A的对应点P的坐标 .(2)、将△ABC绕坐标原点O逆时针旋转90°,直接写出点A的对应点Q的坐标 .(3)、请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标 .32. 如图是游乐园的一角. (1)、如果用(3,2)表示跳跳床的位置,那么跷跷板用表示,碰碰车用表示,摩天轮用表示.
(1)、如果用(3,2)表示跳跳床的位置,那么跷跷板用表示,碰碰车用表示,摩天轮用表示.
(2)、秋千在大门以东400 m,再往北300 m处,请你在图中标出秋千的位置.
33. 如图,在平面直角坐标系中有两点A,B (1)、尺规作图,在x轴上找一点C,使得AC+BC最小:(尺规作图,不写作法,保留作图痕迹);(2)、若A的坐标为(﹣2,1),B的坐标为(3,5)在x轴上找一点C,使得AC+BC最小,求点C的坐标.34. 在平面直角坐标系xOy中,点A的坐标为(1,0),P是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).(1)、点( , )的“双角坐标”为;(2)、若点P到x轴的距离为 ,则m+n的最小值为 .35. 如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1 , D三点的坐标分别是(0,4),(0,3),(0,2).
(1)、尺规作图,在x轴上找一点C,使得AC+BC最小:(尺规作图,不写作法,保留作图痕迹);(2)、若A的坐标为(﹣2,1),B的坐标为(3,5)在x轴上找一点C,使得AC+BC最小,求点C的坐标.34. 在平面直角坐标系xOy中,点A的坐标为(1,0),P是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).(1)、点( , )的“双角坐标”为;(2)、若点P到x轴的距离为 ,则m+n的最小值为 .35. 如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1 , D三点的坐标分别是(0,4),(0,3),(0,2). (1)、求对称中心的坐标.(2)、写出顶点B,C,B1 , C1的坐标.36. 已知:平面直角坐标系中,四边形OABC的顶点分别为O(0,0)、A(5,0)、B(m,2)、C(m﹣5,2).(1)、问:是否存在这样的m,使得在边BC上总存在点P,使∠OPA=90°?若存在,求出m的取值范围;若不存在,请说明理由.(2)、当∠AOC与∠OAB的平分线的交点Q在边BC上时,求m的值.37. 问题情境:
(1)、求对称中心的坐标.(2)、写出顶点B,C,B1 , C1的坐标.36. 已知:平面直角坐标系中,四边形OABC的顶点分别为O(0,0)、A(5,0)、B(m,2)、C(m﹣5,2).(1)、问:是否存在这样的m,使得在边BC上总存在点P,使∠OPA=90°?若存在,求出m的取值范围;若不存在,请说明理由.(2)、当∠AOC与∠OAB的平分线的交点Q在边BC上时,求m的值.37. 问题情境:在平面直角坐标系xOy中有不重合的两点A(x1 , y1)和点B(x2 , y2),小明在学习中发现,若x1=x2 , 则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2 , 则AB∥x轴,且线段AB的长度为|x1﹣x2|;
 (1)、(应用):
(1)、(应用):①若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为.
②若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为.
(2)、(拓展):我们规定:平面直角坐标系中任意不重合的两点M(x1 , y1),N(x2 , y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
①如图1,已知E(2,0),若F(﹣1,﹣2),则d(E,F);
②如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t=.
③如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)=.
38. 每个小方格都是边长为1的正方形,在平面直角坐标系中. (1)、写出图中从原点O出发,按箭头所指方向先后经过的A、B、C、D、E这几个点点的坐标;(2)、按图中所示规律,找到下一个点F的位置并写出它的坐标.
(1)、写出图中从原点O出发,按箭头所指方向先后经过的A、B、C、D、E这几个点点的坐标;(2)、按图中所示规律,找到下一个点F的位置并写出它的坐标.