备考2022年中考数学一轮复习(湘教版)专题24 一元一次不等式组
试卷更新日期:2021-09-22 类型:一轮复习
一、单选题
-
1. 若关于x的不等式组 恰有3个整数解,则实数a的取值范围是( )A、 B、 C、 D、2. 在一元一次不等式组 的解集中,整数解的个数是( )A、4 B、5 C、6 D、73. 不等式1<2x-3<x+1的解集是( )A、1<x<2 B、2<x<3 C、2<x<4 D、4<x<54. 不等式组 的解集在以下数轴表示中正确的是( )A、
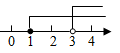 B、
B、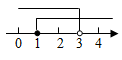 C、
C、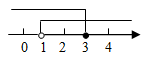 D、
D、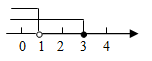 5. 解不等式组 时,不等式①②的解集在同一条数轴上表示正确的是( )A、
5. 解不等式组 时,不等式①②的解集在同一条数轴上表示正确的是( )A、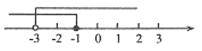 B、
B、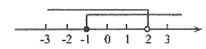 C、
C、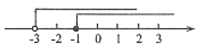 D、
D、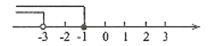 6. 不等式组 的解集,在数轴上表示正确的是( )A、
6. 不等式组 的解集,在数轴上表示正确的是( )A、 B、
B、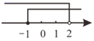 C、
C、 D、
D、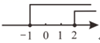 7. 不等式组 的解集表示在数轴上正确的是( )A、
7. 不等式组 的解集表示在数轴上正确的是( )A、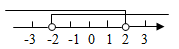 B、
B、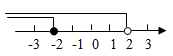 C、
C、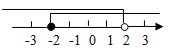 D、
D、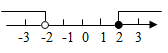 8. 已知不等式组 ,其解集在数轴上表示正确的是( )A、
8. 已知不等式组 ,其解集在数轴上表示正确的是( )A、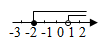 B、
B、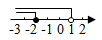 C、
C、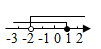 D、
D、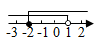 9. 不等式组 的整数解的和为( )A、1 B、0 C、-1 D、-210. 不等式组 的解集在数轴上可表示为( )A、
9. 不等式组 的整数解的和为( )A、1 B、0 C、-1 D、-210. 不等式组 的解集在数轴上可表示为( )A、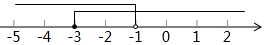 B、
B、 C、
C、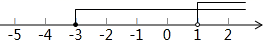 D、
D、
二、填空题
-
11. 如果关于x的不等式组 恰有2个整数解,则a的取值范围是.12. 不等式组 的解集是.13. 已知x满足不等式组 ,写出一个符合条件的x的值 .14. 不等式组 的解集是.15. 不等式 的正整数解为.16. 不等式组 无解,则m的取值范围 .17. 不等式组 的解为.18. 不等式组 的解集是 .19. 若关于x的不等式组 ,有且只有2个整数解,则a的取值范围是 .20. 关于x的一元一次不等式组 有解,则a的取值范围是 .
三、计算题
-
21. 解不等式组:22. 解不等式组: .23. 解不等式组:24. 解不等式组 .25. 解不等式组:
四、解答题
-
26. 解不等式组: ,并在数轴上表示它的解集.
 27. 取哪些正整数值时,不等式 与 都成立?28. 解不等式组 ,并把解集在数轴上表示出来.
27. 取哪些正整数值时,不等式 与 都成立?28. 解不等式组 ,并把解集在数轴上表示出来. 29. 解不等式组 ,并把解集在数轴上表示出来.30. 以下是圆圆解不等式组
29. 解不等式组 ,并把解集在数轴上表示出来.30. 以下是圆圆解不等式组的解答过程:
解:由①,得 , 所以
由②,得 , 所以 , 所以
所以原不等式组的解是 。
圆圆的解答过程是否有错误?如果有错误,请写出正确的解答过程。
31. 解不等式组: ,并将解集在数轴上表示出来. 32. 解不等式组:
32. 解不等式组:五、综合题
-
33. 解不等式组 请按下列步骤完成解答.(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来;
 (4)、原不等式组的解集是.34. 解不等式组
(4)、原不等式组的解集是.34. 解不等式组请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得;
(Ⅱ)解不等式②,得;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:;

(Ⅳ)原不等式组的解集为 .
35. 解不等式组请结合题意填空,完成本题的解答
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来 (4)、原不等式的解集为 .36. 解不等式组 请按下列步骤完成解答:(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来;(4)、原不等式组的解集为.37. 某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆12万元,面包车每辆8万元,公司可投入的购车款不超过100万元;(1)、符合公司要求的购买方案有几种?请说明理由;(2)、如果每辆轿车的日租金为250元,每辆面包车的日租金为150元,假设新购买的这10辆车每日都可租出,要使这10辆车的日租金不低于2000元,那么应选择以上哪种购买方案?38. 一个四位数,记千位数字与个位数字之和为 ,十位数字与百位数字之和为 ,如果 ,那么称这个四位数为“对称数”(1)、最小的“对称数”为;四位数 与 之和为最大的“对称数”,则 的值为;(2)、一个四位的“对称数” ,它的百位数字是千位数字 的 倍,个位数字与十位数字之和为 ,且千位数字 使得不等式组 恰有 个整数解,求出所有满足条件的“对称数” 的值.39. 为迎接边境贸易博览会,组织部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.(1)、某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.(2)、若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
(4)、原不等式的解集为 .36. 解不等式组 请按下列步骤完成解答:(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来;(4)、原不等式组的解集为.37. 某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆12万元,面包车每辆8万元,公司可投入的购车款不超过100万元;(1)、符合公司要求的购买方案有几种?请说明理由;(2)、如果每辆轿车的日租金为250元,每辆面包车的日租金为150元,假设新购买的这10辆车每日都可租出,要使这10辆车的日租金不低于2000元,那么应选择以上哪种购买方案?38. 一个四位数,记千位数字与个位数字之和为 ,十位数字与百位数字之和为 ,如果 ,那么称这个四位数为“对称数”(1)、最小的“对称数”为;四位数 与 之和为最大的“对称数”,则 的值为;(2)、一个四位的“对称数” ,它的百位数字是千位数字 的 倍,个位数字与十位数字之和为 ,且千位数字 使得不等式组 恰有 个整数解,求出所有满足条件的“对称数” 的值.39. 为迎接边境贸易博览会,组织部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.(1)、某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.(2)、若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?