备考2022年中考数学一轮复习（湘教版）专题21 一元二次方程的应用

试卷更新日期：2021-09-22 类型：一轮复习

进入出卷网下载

一、单选题

1. 某校八年级组织一次篮球赛，各班均组队参赛，赛制为单循环形式（每两班之间都赛一场），共需安排15场比赛，则八年级班级的个数为（）

A、5 B、6 C、7 D、8

查看试题解析
2. 为执行国家药品降价政策，给人民群众带来实惠，某药品经过两次降价，每盒零售价由16元降为9元，设平均每次降价的百分率是x，则根据题意，下列方程正确的是（）

A、16（1﹣x）²＝9 B、9（1+x）²＝16 C、16（1﹣2x）＝9 D、9（1+2x）＝16

查看试题解析
3. 随着生产技术的进步，某制药厂生产成本逐年下降.两年前生产一吨药的成本是5000元，现在生产一吨药的成本是4050元.设生产成本的年平均下降率为 $x$ ，下面所列方程正确的是（）

A、 $5000 {(1 + x)}^{2} = 4050$ B、 $4050 {(1 + x)}^{2} = 5000$ C、 $5000 {(1 - x)}^{2} = 4050$ D、 $4050 {(1 - x)}^{2} = 5000$

查看试题解析
4. 某市2018年底森林覆盖率为63%.为贯彻落实“绿水青山就是金山银山”的发展理念，该市大力开展植树造林活动，2020年底森林覆盖率达到68%，如果这两年森林覆盖率的年平均增长率为x，那么，符合题意的方程是（）

A、 $0.63 (1 + x) = 0.68$ B、 $0.63 {(1 + x)}^{2} = 0.68$ C、 $0.63 (1 + 2 x) = 0.68$ D、 $0.63 {(1 + 2 x)}^{2} = 0.68$

查看试题解析
5. 在育红学校开展的课外阅读活动中，学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字．设该校七至九年级人均阅读量年均增长率为x ，根据题意，所列方程正确的是（）

A、 $100 {(1 + x)}^{2} = 121$ B、 $100 \times 2 (1 + x) = 121$ C、 $100 (1 + 2 x) = 121$ D、 $100 (1 + x) + 100 {(1 + x)}^{2} = 121$

查看试题解析
6. “杂交水稻之父”袁隆平和他的团队探索培育的“海水稻”在某试验田的产量逐年增加，2018年平均亩产量约500公斤，2020年平均亩产量约800公斤．若设平均亩产量的年平均增长率为x ，根据题意，可列方程为（）

A、 $500 (1 + x) = 800$ B、 $500 (1 + 2 x) = 800$ C、 $500 (1 + x^{2}) = 800$ D、 $500 {(1 + x)}^{2} = 800$

查看试题解析
7. 随着互联网技术的发展，我国快递业务量逐年增加，据统计从2018年到2020年，我国快递业务量由507亿件增加到833.6亿件，设我国从2018年到2020年快递业务量的年平均增长率为x ，则可列方程为（）

A、 $507 (1 + 2 x) = 833.6$ B、 $507 \times 2 (1 + x) = 833.6$ C、 $507 {(1 + x)}^{2} = 833.6$ D、 $507 + 507 (1 + x) + 507 {(1 + x)}^{2} = 833.6$

查看试题解析

二、填空题

8. 某单位有10000名职工，想通过验血的方式筛查出某种病毒的携带者．如果对每个人的血样逐一化验，需要化验10000次．统计专家提出了一种化验方法：随机地按5人一组分组，然后将各组5个人的血样混合再化验．如果混合血样呈阴性，说明这5个人全部阴性；如果混合血样呈阳性，说明其中至少有一个人呈阳性，就需要对这组的每个人再分别化验一次．假设携带该病毒的人数占0.05%．回答下列问题：

(1)、按照这种化验方法是否能减少化验次数（填“是”或“否”）；

(2)、按照这种化验方法至多需要次化验，就能筛查出这10000名职工中该种病毒的携带者．

查看试题解析
9. 为把我市创建成全国文明城市，某社区积极响应市政府号召，准备在一块正方形的空地上划出部分区域栽种鲜花，如图中的阴影“┛”带，鲜花带一边宽1m.另一边宽2m，剩余空地的面积为18m² ，求原正方形空地的边长 $x$ m，可列方程为.

查看试题解析
10. 某种服装原价每件80元，经两次降价，现售价每件64.8元，这种服装平均每次降价的百分率是.

查看试题解析
11. 由10块相同的小长方形地砖拼成面积为1.6m²的长方形ABCD（如图），则长方形ABCD的周长为．

查看试题解析
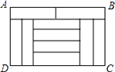12. 在党中央的正确领导和全国人民的共同努力下，我国新冠肺炎确诊人数逐日下降，同时为构建人类命运共同体，我国积极派出医疗队帮助其他国家抗疫，由我国援助的Y国刚开始每周新增新冠肺炎确诊人数是2500人，两周后每周新增新冠肺炎确诊人数是1600人，若平均每周下降的百分率相同，则平均每周下降的百分率是．

查看试题解析
13. 某中学有一块长30m，宽20m的矩形空地，计划在这块空地上划分出四分之一的区域种花，小明同学设计方案如图所示，求花带的宽度．设花带的宽为xm，则可列方程为．

查看试题解析
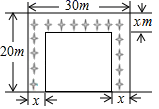14. 某商场八月份的营业额是100万元，预计十月份的营业额可达到144万元，若九、十月份营业额的月增长率相同为 $x$ ，那么由题意可列得方程为

查看试题解析
15. 某电视机制造商2021年一月份生产电视机2000台，2021年三月份生产电视机2420台，设二、三月份每月的平均增长率为x，根据题意，可列方程为.

查看试题解析
16. 甲公司1月份的营业额为60万元，3月份的营业额为100万元，假设该公司2、3两个月的增长率都为x ，那么可列方程是．

查看试题解析
17. 据美国约翰斯•霍普金斯大学发布的全球新冠肺炎数据统计系统，截至美国东部时间3月28日晚6时，全美共报告新冠肺炎确诊人数超过3025万，死亡超过54.9万，已知有一人患了新冠肺炎，经过两轮传染后，共有144人患了新冠肺炎，每轮传染中平均每人传染了人.

查看试题解析

三、解答题

18. 某商品一月份价格为a元/件，二月份降价，三月份又涨价，涨价后恢复到一月份的价格．如果三月份涨价的百分比是二月份降价百分比的2倍，求二月份降价的百分比．

查看试题解析
19. 目前，以5G为代表的战略性新兴产业蓬勃发展．某市2019年底有5G用户2万户，计划到2021年底5G用户数累计达到8.72万户．求这两年全市5G用户数的年平均增长率．

查看试题解析
20. 读诗词解题：（通过列方程式，算出周瑜去世时的年龄）
大江东去浪淘尽，千古风流数人物；

而立之年督东吴，早逝英年两位数；

十位恰小个位三，个位平方与寿符；

哪位学子算得快，多少年华属周瑜？

查看试题解析
21. 某商场出售的电脑原价为每台5000元，元旦期间开展了促销活动，将原价经过两次下调后，促销价为每台4050元．

(1)、求平均每次下调的百分率；

(2)、临近春节，该店决定推出力度更大的促销活动，按（1）中的百分率第三次下调销售价，若该电脑的进货价为每台3000元，则此次促销中每台电脑的利润为元．

查看试题解析
22. 如图，在足够大的空地上有一段长为 $3 m$ 的旧墙 $M N$ ，某人利用旧墙和木栏围成一个矩形菜园 $A B C D$ ，其中 $A D \leq M N$ .已知矩形菜园的一边靠墙，修筑另三边一共用了 $16 m$ 木栏.若所围成的矩形菜园的面积为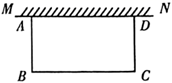 $14 m^{2}$ ，求 $A D$ 的长.

查看试题解析
23. 平遥牛肉久负盛名．据史料记载，清代时已誉满三晋．其制作工艺独特，用料讲究，所产牛肉营养丰富，具有扶胃健脾之功效．某特产店以每千克110元的价格购进一批平遥牛肉，当按每千克140元的价格出售时，平均每天可销售30千克．“十一”期间，为了尽可能扩大销售量，商家决定降价销售．经调查发现，每千克降价1元，每天可多卖2千克．若该经销商想要每天获利1000元，则每千克应降价多少元？

查看试题解析
24. 某商店销售一种服装，已知该服装每件成本为50元.经市场调研，售价为每件60元时，可销售800件；售价每提高5元，销售量将减少100件.
问：商店销售这批服装计划获利12000元，应如何进货？每件售价多少元？

查看试题解析
25. 某服装经营户以20元/件的价格购进一批衣服，以30元/件的价格出售，每天可售出20件.为了促销，该经营户决定降价销售，经调查发现，这种衣服每件降价1元，每天可多售出5件.另外，每天的房租等固定成本共25元，该经营户要想每天盈利200元，应将每件衣服的售价降低多少元？

查看试题解析
26. 如图，一农户要建一个矩形猪舍，猪舍的一边利用长为12米的住房墙，另外三边用25米长的建筑材料围成的，为了方便进出，在垂直于住房墙的一边留一扇1米宽的门.当所围矩形与墙垂直的一边长为多少时，猪舍面积为80平方米？

查看试题解析

四、综合题

27. 为做好延迟开学期间学生的在线学习服务工作，市教育局推出“中小学延迟开学期间网络课堂”，为学生提供线上学习，据统计，第一批公益课受益学生20万人次，第三批公益课受益学生24.2万人次．

(1)、如果第二批，第三批公益课受益学生人次的增长率相同，求这个增长率；

(2)、按照这个增长率，预计第四批公益课受益学生将达到多少万人次？

查看试题解析
28. 某服装店自2018年以来，销售成衣数量在稳健地上涨，2018年全年售出10000件成衣，2020年全年售出14400件成衣．

(1)、求该服装店2018年到2020年成衣销售量的年平均增长率；

(2)、若服装店售出成衣数量还将保持相同的年平均增长率，请你预算2022年该服装店售出成衣将达到多少件?

查看试题解析
29. 学海书店购一批故事书进行销售，其进价为每本40元，如果按每本故事书50元进行出售，每月可以售出500本故事书，后来经过市场调查发现，若每本故事书涨价1元，则故事书的销量每月减少20本．

(1)、若学海书店要保证每月销售此种故事书盈利6000元，同时又要使购书者得到实惠，则每本故事书需涨价多少元？

(2)、若使该故事书的月销量不低于300本，则每本故事书的售价应不高于多少元？

查看试题解析
30. 某市某水果批发市场某批发商原计划以每千克10元的单价对外批发销售某种水果．为了加快销售，该批发商对价格进行两次下调后，售价降为每千克6.4元．

(1)、求平均每次下调的百分率；

(2)、某大型超市准备到该批发商处购买2吨该水果，因数量较多，该批发商决定再给予两种优惠方案以供选择．方案一：打八折销售；方案二：不打折，每吨优惠现金1000元．试问超市采购员选择哪种方案更优惠？请说明理由．

查看试题解析
31. 某零件生产厂生产的某型号零件1月份平均日产量为2000个，由于市场需求量大增，工厂决定从2月份起扩大产能，3月份平均日产量达到2420个．假设该型号零件2，3，4每个月平均日产量增长率相同．

(1)、求该型号零件日产量的月平均增长率；

(2)、预计4月份该型号零件平均日产量为多少个？

查看试题解析
32. 春节期间，佛山连锁超市派调查小组调查某种商品的销售情况，下面是调查后小李与其他两位成员交流的情况．
小李：“该商品的进价为50元/件．”

成员甲：“当定价为60元/件时，平均每天可售出800件．”

成员乙：“若售价每提高5元，则平均每天少售出100件．”

根据他们的对话，完成下列问题：

(1)、若售价定为65元/件时，平均每天可售出件；

(2)、若超市希望该商品平均每天能盈利12000元，且尽可能扩大销售量，则该商品应该怎样定价？

查看试题解析
33. 去年某商店“五一黄金周”进行促销活动期间，前四天的总营业额为300万元，第五天的营业额是前四天总营业额的20%．

(1)、求该商店去年“五一黄金周”这五天的总营业额；

(2)、今年，该商店3月份的营业额为350万元，预计今年4、5月份营业额的月增长率基本相同，5月份的营业额比去年“五一黄金周”这5天的总营业额增长了40%．求该商店今年4、5月份营业额的月增长率．

查看试题解析
34. 机械加工需要用油进行润滑以减小摩擦，某企业加工一台大型机械设备润滑用油量为90千克，用油的重复利用率为60%，按此计算，加工一台大型机械设备的实际耗油量为36千克，为了建设节约型社会，减少油耗，该企业的甲、乙两个车间都组织了人员为减少实际耗油量进行攻关.

(1)、甲车间通过技术革新后，加工一台大型机械设备润滑用油量下降到70千克，用油量的重复利用率仍然为60%.问甲车间技术革新后，加工一台大型机械设备的实际耗油量是多少千克？

(2)、乙车间通过技术革新后，不仅降低了润滑用油量，同时也提高了用油的重复利用率，并且发现在技术革新前的基础上，润滑用油量每减少1千克，用油的重复利用率将增加1.6%，这样乙车间加工一台大型机械设备的实际耗油量下降到12千克，问乙车间技术革新后，加工一台大型机械设备的润滑用油量是多少千克？用油的重复利用率是多少？

查看试题解析
35. 为积极响应国家“旧房改造”工程，该市推出《加快推进旧房改造工作的实施方案》推进新型城镇化建设，改善民生，优化城市建设.

(1)、根据方案该市的旧房改造户数从2020年底的3万户增长到2022年底的4.32万户，求该市这两年旧房改造户数的平均年增长率；

(2)、该市计划对某小区进行旧房改造，如果计划改造300户，计划投入改造费用平均20000元/户，且计划改造的户数每增加1户，投入改造费平均减少50元/户，求旧房改造申报的最高投入费用是多少元？

查看试题解析
36. 某超市经过记录发现近期龙眼的日销售量 $y$ （kg）与售价 $x$ （元/kg）有下表关系：

$x$

10

12

15

20

$y$

196

176.4

147

98

(1)、请直接回答以上数据符合一次函数、反比例函数或二次函数中的哪一种？并求出 $y$ 与 $x$ 之间的函数解析式；

(2)、已知龙眼的进货价是8元/kg，售价不能超过进货价的2倍，经调查平均每100kg龙眼会有2kg损耗，如果希望龙眼的每日利润是1005元，那么龙眼的售价应该定为多少元/kg？

查看试题解析

$x$	10	12	15	20
$y$	196	176.4	147	98