备考2022年中考数学一轮复习（湘教版）专题38 垂线与两条平行线间的距离

试卷更新日期：2021-09-22 类型：一轮复习

进入出卷网下载

一、单选题

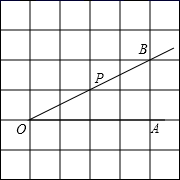
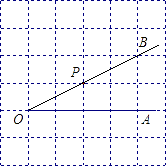
1. 如图，设点P是直线 $l$ 外一点，PQ⊥ $l$ ，垂足为点Q，点T是直线 $l$ 上的一个动点，连结PT，则（）

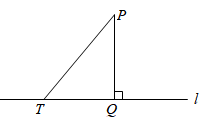A、PT≥2PQ B、PT≤2PQ C、PT≥PQ D、PT≤PQ

查看试题解析
2. 如图，在平面内作已知直线m的垂线，可作垂线的条数有（）

A、0条 B、1条 C、2条 D、无数条

查看试题解析
3. 若线段AM，AN分别是△ABC边上的高线和中线，则（）

A、 $A M > A N$ B、 $A M \geq A N$ C、 $A M < A N$ D、 $A M \leq A N$

查看试题解析
4. 已知△ABC中，BC=6，AC=3，CP⊥AB，垂足为P，则CP的长可能是（）

A、2 B、4 C、5 D、7

查看试题解析
5. 如图，直线EO⊥CD，垂足为点O，AB平分∠EOD，则∠BOD的度数为（　　）

A、120° B、130° C、135° D、140°

查看试题解析
6. 已知直线a∥b∥c，a与b的距离为5cm，b与c的距离为2cm，则a与c的距离是（）

A、3cm B、7cm C、3cm或7cm D、以上都不对

查看试题解析
7. 用直尺和圆规作Rt△ABC斜边AB上的高线CD，以下四个作图中，作法错误的是（　　）

A、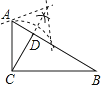 B、 C、 D、

查看试题解析
8.
如图，△ABC是锐角三角形，过点C作CD⊥AB，垂足为D，则点C到直线AB的距离是（　　）

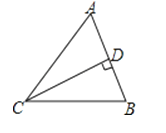A、线段CA的长 B、线段CD的长 C、线段AD的长 D、线段AB的长

查看试题解析
9.
如图，△ABC中，∠C=90°，AC=3，点P是边BC上的动点，则AP长不可能是( )

A、2.5 B、3 C、4 D、5

查看试题解析

二、填空题

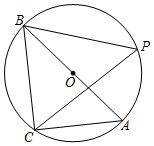
10. 设 $A B$ ， $C D$ ， $E F$ 是同一平面内三条互相平行的直线，已知 $A B$ 与 $C D$ 的距离是 $12 c m$ ， $E F$ 与 $C D$ 的距离是 $5 c m$ ，则 $A B$ 与 $E F$ 的距离等于 $c m$ .

查看试题解析
11. 如图， $Δ A B C$ 是⊙O的内接三角形，且AB是⊙O的直径，点P为⊙O上的动点，且 $∠ B P C = 60^{°}$ ，⊙O的半径为6，则点P到AC距离的最大值是．

查看试题解析
12. 如图，点A，B，C在直线l上，PB⊥l ， PA=6cm，PB=5cm，PC=7cm，则点P到直线l的距离是cm.

查看试题解析
13. 如图，直线AB，CD相交于点O，EO⊥AB于点O，∠EOD=50°，则∠BOC的度数为．

查看试题解析
14. 如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD= $3 \sqrt{2}$ ，CD= $2 \sqrt{2}$ ，点P是四边形ABCD四条边上的一个动点，若P到BD的距离为 $\frac{5}{2}$ ，则满足条件的点P有个．

查看试题解析
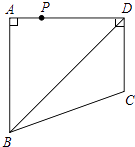15. 图①表示一个时钟的钟面垂直固定于水平桌面上，其中分针上有一点A，当钟面显示3点30分时，分针垂直于桌面，A点距桌面的高度为10cm．图②表示当钟面显示3点45分时，A点距桌面的高度为16cm，若钟面显示3点55分时，A点距桌面的高度为 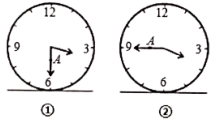$cm$ ．

查看试题解析

三、作图题

16. 如图，已知 $∠ E B C = 30 °$ ，点 $A$ 为边 $B E$ 上一点，请用尺规在 $B C$ 边上作一点 $D$ ，使得 $B D = 2 A D$ （要求：保留作图痕迹，不写作法和证明）

查看试题解析
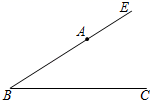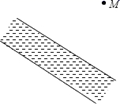
17. 如图，在4×5的正方形网格中，每个小正方形的边长为1，点AB在格点上，点C是线段AB与格线的交点。利用网格和无刻度的直尺按下列要求画图。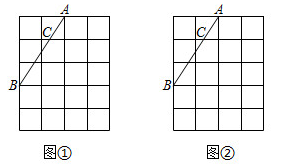

(1)、在图①中，过点B作AB的垂线。

(2)、在图②中，过点C作AB的垂线。

查看试题解析
18. 如图，某村庄计划把河中的水引到水池M中，怎样开的渠最短，为什么（保留作图痕迹，不写作法和证明）
理由是：．

查看试题解析

四、解答题

19. 如图，已知直线 $A B$ 和 $C D$ 相交于O点，射线 $O E ⊥ A B$ 于O，射线 $O F ⊥ C D$ 于O，且 $∠ B O F = 20 °$ .求 $∠ E O D$ 的度数.

查看试题解析
20. 如图，直线AB、CD相交于点O，EO⊥AB，垂足为O，∠EOC：∠AOD=7：11，求∠DOE的度数.

查看试题解析
21. 如图，某村庄计划把河中的水引到水池M中，怎样开的渠最短，为什么？（保留作图痕迹，不写作法和证明）
理由是： ▲ .

查看试题解析

五、综合题

22. 阅读理解题
在平面直角坐标系xOy中，点P（x₀ ， y₀）到直线Ax+By+C=0（A²+B²≠0）的距离公式为：d= $\frac{| A x_{0} + B y_{0} + C |}{\sqrt{A^{2} + B^{2}}}$ ，
例如，求点P（1，3）到直线4x+3y﹣3=0的距离．
解：由直线4x+3y﹣3=0知：A=4，B=3，C=﹣3
所以P（1，3）到直线4x+3y﹣3=0的距离为：d= $\frac{| 4 \times 1 + 3 \times 3 - 3 |}{\sqrt{4^{2} + 3^{2}}}$ =2
根据以上材料，解决下列问题：

(1)、求点P₁（0，0）到直线3x﹣4y﹣5=0的距离．

(2)、若点P₂（1，0）到直线x+y+C=0的距离为 $\sqrt{2}$ ，求实数C的值．

查看试题解析
23.

(1)、如图，过点A画直线BC的垂线，并注明垂足为G；过点A画直线AB的垂线，交BC于点H.

(2)、线段的长度是点A到直线BC的距离.

(3)、线段AG、AH的大小关系为AGAH.（用符号>，<，=， $\geq ， \leq$ 表示）.理由是.

查看试题解析
24. 如图，点P是∠AOB的边OB上的一点．

(1)、①过点P画OB的垂线，交OA于点C；
②过点P画OA的垂线，垂足为H；

(2)、线段PH的长度是点P到的距离，是点C到直线OB的距离，线段PC、PH、OC这三条线段大小关系是（用“＜”号连接）．

查看试题解析
25. 如图，点P是∠AOB的边OB上的一点过点P画OB的垂线，交OA于点C；

(1)、过点P画OA的垂线，垂足为H；

(2)、线段PH的长度是点P到的距离，是点C到直线OB的距离．线段PC、PH、OC这三条线段大小关系是（用“＜”号连接）

查看试题解析